直線と方程式

直線の式

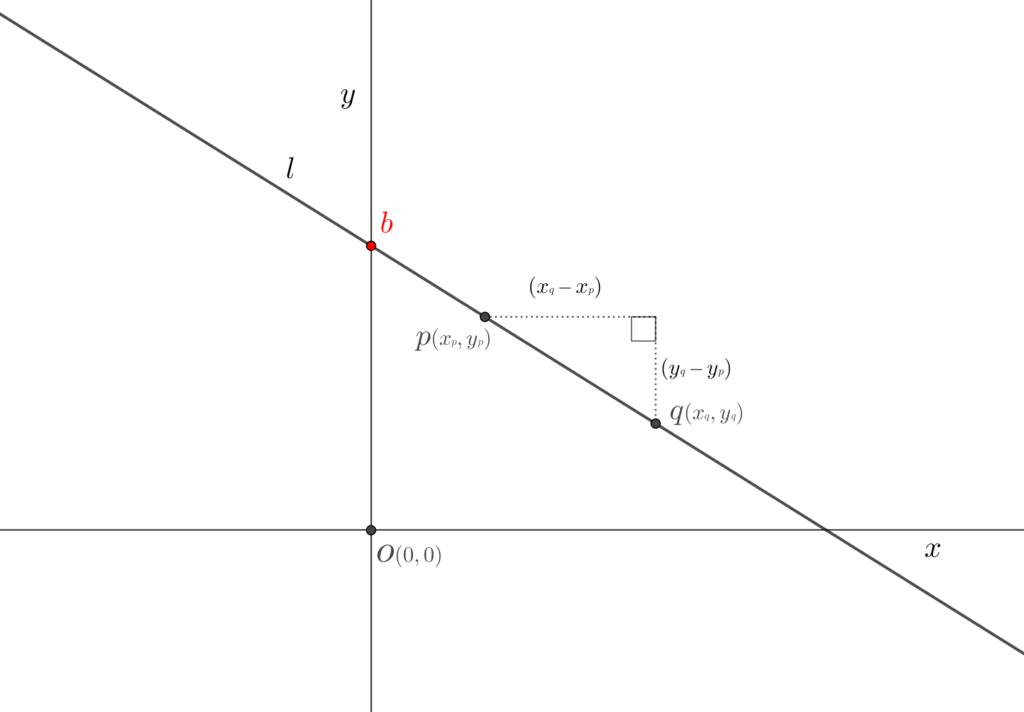
直線\((\small\textsf{$1$次関数})\)の式 \(\hspace{10pt}\)\(y{\scriptsize\,=\,}ax{\scriptsize\,+\,}b\)

図\(1,2\)から、\(y\)軸上の 点\(\color{red}b\) を 切片 という。 直線と\(y\)軸の交点である。直線の式では定数項\(b\)の部分である。

直線\(l\)上に任意の点 \(p,q\) を置く。点\(p\) を移動させ、点\(q\)に重ねた変化の割合を 傾き という。直線の式では \(x\) の係数\(a\)の部分である。

傾きは \(\scriptsize\displaystyle\frac{y\textsf{の増加量}}{x\textsf{の増加量}}\left(\scriptsize{p\:\rightarrow\:q\,=\,}\displaystyle\frac{y{\tiny q}{\scriptsize\,-\,}y{\tiny p}}{x{\tiny q}{\scriptsize\,-\,}x{\tiny p}}\right)\) で求められ、直線\(l\)上を移動する点\(p\)の変化の割合は直線の傾き\(a\)になる。

図\(1\)の直線\(l\)は原点\({\Large o}{\scriptsize (0,0)}\)を通る直線である。切片は\(0\)なので、直線の式は \(y{\scriptsize\,=\,}ax\) になる。

垂直線の傾き

直交する\(2\)直線の 傾き の積は \(-1\) である。

直線 \(\color{gray}l{\scriptsize 1}\) と直線 \(\color{gray}l{\scriptsize 2}\) は直交する\((\)互いに垂直線である\()\)。

直線を平行移動してもその 傾き は変わらないので、\(2\)直線\(\color{gray}l{\scriptsize 1},\color{gray}l{\scriptsize 2}\)を平行移動して \(l^{\prime}{\scriptsize 1},l^{\prime}{\scriptsize 2}\) とし、その直交点を原点 \(O\) とする。\(\hspace{15pt}\)\((\)\(\small\leftarrow\) 解説を容易にするため\()\)

直角三角形 \(Opq\) から、\(\href{https://showanojoe.com/template-math/trigonometric-function/three-squares-theorem/}{\color{teal}\textsf{三平方の定理 }}\) により 係数\(m,n\) を導出してその積が \(-1\) であることを確認するのが課題となる。

直角三角形 \(Opq\) の斜辺\(pq\)の長さを \(2\)点間の距離で算出すると、\(pq{\small\;=\;}(1{\small -}1,m{\small -}n){\small \;=\,}(0,\,m{\small\,-\,}n)\hspace{10pt}{\small\rightarrow}\hspace{10pt}|m-n| \) となる。

辺 \(Op,Oq\) の長さ\((\)\(2\)点間の距離\()\)は\(p-O,q-O{\scriptsize\;=\;}(1-0,m-0),(1-0,n-0)\) を三平方の定理から

\(\left\{\begin{array}{l}(1{\small\,-\,}0)^{\scriptsize 2}{\small\,+\,}(m{\small\,-\,}0)^{\scriptsize 2}{\small\;=\;}(Op)^{\scriptsize 2} \\ (1{\small\,-\,}0)^{\scriptsize 2}{\small\,+\,}(n{\small\,-\,}0)^{\scriptsize 2}{\small\,=\,}(Oq)^{\scriptsize 2}\end{array}\right.\) \(\hspace{10pt}\) \(\left\{\begin{array}{l}1{\small\,+\,}m^{\scriptsize 2}{\small\,+\,}1{\small\,+\,}n^{\scriptsize 2}{\small\;=\;}(m{\small\,-\,}n)^{\scriptsize 2}\\ \hspace{50pt}{\small\downarrow} \\ 1+m^{\scriptsize 2}{\small\,+\,}1{\small\,+\,}n^{\scriptsize 2}{\small\;=\;}m^{\scriptsize 2}{\small\,-\,}2mn{\small\,+\,}n^{\scriptsize 2} \\ \hspace{50pt}{\small\downarrow}\;\small\textsf{整理すると}\\ mn{\small\;=\;}{\small\,-\,}1\end{array}\right. \)

直線\(\color{gray}l{\tiny 1}\) の式が \(y{\scriptsize\,=\,}\small -\displaystyle\frac{2}{7}{\normalsize x}{\scriptsize\,+\,}{\normalsize b}\)　ならば、直交する直線\(\color{gray}l{\tiny 2}\) の式は \(y{\scriptsize\,=\,}\small \displaystyle\frac{7}{2}{\normalsize x}{\scriptsize\,+\,}{\normalsize b}\) となる。

点と直線の距離

原点と直線の距離

\(\cssId{2-1}{\textsf{直線の方程式$(\textsf{傾きと切片が整数ではない})$には二つの形式があり}}\) \(y{\scriptsize\,=\,}\)\({\small\displaystyle\frac{a}{b}}\)\(x{\scriptsize\,+\,}\)\({\small\displaystyle\frac{c}{b}}\) の 基本形 と \(ax{\scriptsize\,-\,}by{\scriptsize\,+\,}c{\scriptsize\,=\,}0\) の 一般形 で表せる。

直線に直交する垂直線の式は 前節の\(\href{#2}{\color{teal}\textsf{垂直線の傾き}}\) から \(y{\scriptsize\,=\,}{\small-\displaystyle\frac{b}{a}}x\)　となる。

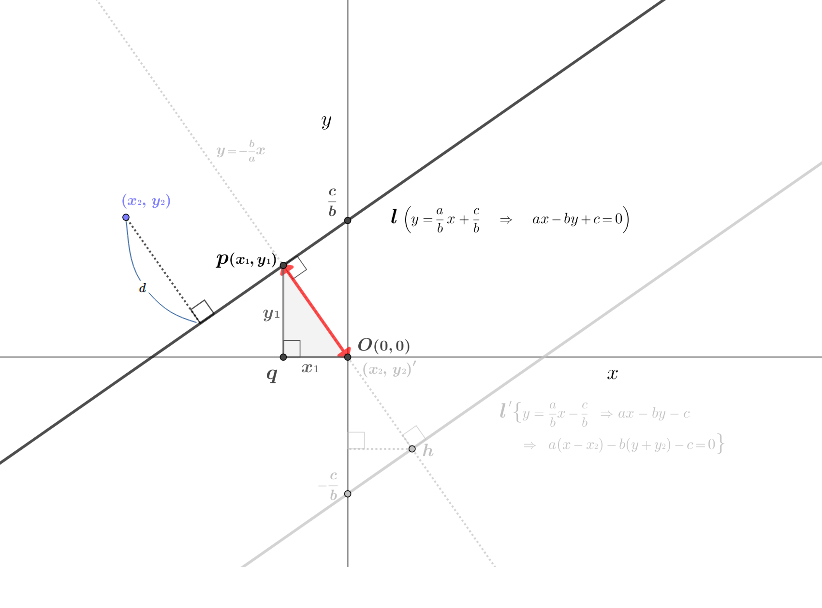
図\(4\)から、原点と直線間の距離 は原点\(O\)から直線\(l\)に引いた赤い垂線\((\)線分\(Op\)\()\) の長さを求めることである。

直線\(l\) の垂直線は直交点\(p(x{\tiny 1},y{\tiny 1})\)を通るので、\(l\) は \(y{\tiny 1}{\scriptsize\,=\,}{\small\displaystyle\frac{a}{b}}x{\tiny 1}{\scriptsize\,+\,}{\small\displaystyle\frac{c}{b}}\) と \(ax{\tiny 1}{\scriptsize\,-\,}by{\tiny 1}{\scriptsize\,+\,}c{\scriptsize\,=\,}0\)、その垂直線は\(y{\tiny 1}{\scriptsize\,=\,}{\small-\displaystyle\frac{b}{a}}x{\tiny 1}\) の式で表せる。

垂直線 \(y{\tiny 1}{\scriptsize\,=\,}{\small-\displaystyle\frac{b}{a}}x{\tiny 1}\) は、\(x{\tiny 1}{\scriptsize\,=\,}{\small-\displaystyle\frac{a}{b}}y{\tiny 1}\) に式変形できる。この\(x{\tiny 1},y{\tiny 1}\)の単項式を直線\(l\)の一般形の式に代入すると、

\(\hspace{80pt}\textsf{}\left\{\begin{array}{l}ax{\tiny 1}{\scriptsize\,-\,}b\left({\small-\displaystyle\frac{b}{a}}x{\tiny 1}\right){\scriptsize\,+\,}c{\scriptsize\,=\,}0\hspace{10pt}{\small \rightarrow}\hspace{10pt}ax{\tiny 1}{\scriptsize\,+\,}{\small\displaystyle\frac{\:\,b^{\tiny 2}}{a}}x{\tiny 1}{\scriptsize\,+\,}c{\scriptsize\,=\,}0\hspace{10pt}{\small \rightarrow}\hspace{10pt}{\small\displaystyle\frac{a^{\tiny 2}{\scriptsize\,+\,} b^{\tiny 2}}{a}}x{\tiny 1}{\scriptsize\,-\,}c{\small\,=\,}0\hspace{10pt}{\small \rightarrow}\hspace{10pt}x{\tiny 1}{\scriptsize\,=\,}{\small-\displaystyle\frac{ac}{a^{\tiny 2}{\scriptsize\,+\,} b^{\tiny 2}}} \\ a\left({\small-\displaystyle\frac{a}{b}}y{\tiny 1}\right){\scriptsize\,-\,}by{\tiny 1}{\scriptsize\,+\,}c{\scriptsize\,=\,}0\hspace{10pt}{\small \rightarrow}\hspace{10pt}{\scriptsize\,-\,}{\small\displaystyle\frac{\:\,a^{\tiny 2}}{b}}y{\tiny 1}{\scriptsize\,+\,}by{\tiny 1}{\scriptsize\,+\,}c{\scriptsize\,=\,}0\hspace{10pt}{\small \rightarrow}\hspace{10pt}{\small\displaystyle\frac{a^{\tiny 2}{\scriptsize\,+\,} b^{\tiny 2}}{b}}y{\tiny 1}{\scriptsize\,-\,}c{\small\,=\,}0\hspace{10pt}{\small \rightarrow}\hspace{10pt}y{\tiny 1}{\scriptsize\,=\,}{\small-\displaystyle\frac{bc}{a^{\tiny 2}{\scriptsize\,+\,} b^{\tiny 2}}}\end{array}\right.\hspace{40pt}\)となる。

\(\hspace{150pt}\)ちなみに、直線\(l\)の基本形の式ではなく一般形の式に代入したのは、単に計算しやすいからである。

導出した\(x{\tiny 1}\) と \(y{\tiny 1}\)の実数\(a,b,c\)の式で (直角)三角形\(Opq\) から三平方の定理で線分\(Op\)の長さをも求める。

\(\hspace{80pt}\sqrt{\left(Op\right)^2}{\scriptsize\hspace{10pt}=\;}\scriptsize\sqrt{\left({-\displaystyle\frac{ac}{a^{\tiny 2}{\scriptsize\,+\,} b^{\tiny 2}}}\right)^2}{\scriptsize\,+\,}\sqrt{\left({-\displaystyle\frac{bc}{a^{\tiny 2}{\scriptsize\,+\,} b^{\tiny 2}}}\right)^2}\)\({\scriptsize\;=\;}\scriptsize\sqrt{\left({\displaystyle\frac{a^2 c^2}{(a^{\tiny 2}{\scriptsize\,+\,} b^{\tiny 2})^2}}\right){\scriptsize\,+\,}\left({\displaystyle\frac{b^2 c^2}{(a^{\tiny 2}{\scriptsize\,+\,} b^{\tiny 2})^2}}\right)}\)\({\scriptsize\;=\;}\scriptsize\sqrt{\displaystyle\frac{a^2 c^2 + b^2 c^2}{(a^{\tiny 2}{\scriptsize\,+\,} b^{\tiny 2})^2}}\)\({\scriptsize\;=\;}\scriptsize\sqrt{\displaystyle\frac{(a^2 + b^2) c^2}{(a^{\tiny 2}{\scriptsize\,+\,} b^{\tiny 2})^2}}{\scriptsize\;=\;}\scriptsize\sqrt{\displaystyle\frac{c^2}{a^{\tiny 2}{\scriptsize\,+\,} b^{\tiny 2}}}\)\({\scriptsize\,=\,}{\scriptsize\displaystyle\frac{\sqrt{c^2}}{\sqrt{a^{\tiny 2}{\scriptsize\,+\,} b^{\tiny 2}}}}\)

線分\(Op\)の長さは \({\small\displaystyle\frac{\sqrt{c^2}}{\sqrt{a^{\tiny 2}{\scriptsize\,+\,} b^{\tiny 2}}}}\)、すなわち 原点\(O\)と直線\(l\)間の距離 は \({\small\displaystyle\frac{\sqrt{c^2}}{\sqrt{a^{\tiny 2}{\scriptsize\,+\,} b^{\tiny 2}}}}\hspace{10pt}\Rightarrow\hspace{10pt}{\small\displaystyle\frac{|\,c\,|}{\sqrt{a^{\tiny 2}{\scriptsize\,+\,} b^{\tiny 2}}}}\) になる。

\(\hspace{100pt}\left\{\begin{array}{l}\scriptsize\textsf{$|c|$の$|\cdot|$ は $\href{https://showanojoe.com/template-math/supplementary-material/absolute-value/}{\color{teal}\textsf{絶対値}}$ を表す記号。} \\ \scriptsize\textsf{絶対値の定義}\hspace{5pt}|x|{\scriptsize\:\fallingdotseq\:}max\left\{x,\,{\tiny -}x\right\}\left\{\begin{array}{l}x\hspace{10pt}(x{\tiny\,\geqq\,} 0) \\ {\tiny -}x\hspace{5pt}(x{\tiny\,<\,} 0)\end{array}\right. \\ \hspace{10pt}\scriptsize\textsf{$\fallingdotseq$ は限りなくイコールに近いイコールを意味する記号(ニアリーイコールという)。}\end{array}\right\}\)

原点以外の点と直線の距離

図\(4\)から、では点\(\color{blue}(x{\tiny 2},\,y{\tiny 2})\) と直線\(l\) の距離\(d\) の式は

 点\(\color{blue}(x{\tiny 2},\,y{\tiny 2})\) と直線\(l\) を \(x\) 軸方向に \({\small +}x{\tiny 2}\)、\(y\) 軸方向に \({\small −}y{\tiny 2}\) 平行移動する。直線 \(\color{#C0C0C0}\boldsymbol l^{\prime}\)は \(\color{#C0C0C0}a(x{\small\,-\,}x{\tiny 2}){\small\,-\,}b(y{\small\,+\,}y{\tiny 2}){\small\,+\,}c{\small\,=\,}0\) となるので，原点 \(O\)\(\left\{{\small =\;}{\color{#C0C0C0}(x{\tiny 2},\,y{\tiny 2})^{\prime}}\right\}\) から \(\color{#C0C0C0}\boldsymbol l^{\prime}\) を通る垂直線 \({\color{#C0C0C0}y{\small\;=\;}{\small-\displaystyle\frac{b}{a}}x}\) との交点を \(\color{gray}\boldsymbol h\) とする。

 点\(\color{#C0C0C0}\boldsymbol h\) の座標は \(\color{#C0C0C0}\boldsymbol l^{\prime}\) の式の変数\(y\) に 垂直線 \({\color{#C0C0C0}y{\small\;=\;}{\small-\displaystyle\frac{b}{a}}x}\) を代入した式\((\)連立\(2\)次方程式\()\)になる。
\(\color{#C0C0C0}a(x{\small\,-\,}x{\tiny 2}){\small\,-\,}b(y{\small\,+\,}y{\tiny 2}){\small\,-\,}c{\small\,=\,}0\)\(\hspace{10pt}{\small\Rightarrow}\hspace{10pt}\)\(\color{#C0C0C0}a(x{\small\,-\,}x{\tiny 2}){\small\,-\,}b({{\small-\displaystyle\frac{b}{a}}x}{\small\,+\,}y{\tiny 2}){\small\,-\,}c{\small\,=\,}0\)\(\hspace{10pt}{\small\Rightarrow}\hspace{10pt}\)\(\)\(\color{#C0C0C0}ax{\small\,-\,}ax{\tiny 2}{\small\,+\,}{{\small\displaystyle\frac{b^{2}}{a}}x}{\small\,-\,}by{\tiny 2}{\small\,-\,}c{\small\,=\,}0\)\(\hspace{10pt}{\small\Rightarrow}\hspace{10pt}\)\(\)\(\color{#C0C0C0}a^{2}x{\small\,-\,}a^{2}x{\tiny 2}{\small\,+\,}{{\small{b^{2}}}x}{\small\,-\,}aby{\tiny 2}{\small\,-\,}ac{\small\,=\,}0\)\(\hspace{10pt}{\small\Rightarrow}\hspace{10pt}\)\(\color{#C0C0C0}(a^{2}{\small\,+\,}b^{2})x{\small\,-\,}a^{2}x{\tiny 2}{\small\,-\,}aby{\tiny 2}{\small\,-\,}ac{\small\,=\,}0\)\(\hspace{10pt}{\small\Rightarrow}\hspace{10pt}\)\(\color{#C0C0C0}{\small\,-\,}a^{2}x{\tiny 2}{\small\,-\,}aby{\tiny 2}{\small\,-\,}ac{\small\,=\,}{\small -}(a^{2}{\small\,+\,}b^{2})x\)\(\hspace{10pt}{\small\Rightarrow}\hspace{10pt}\)\(\color{#C0C0C0}x{\small\;=\;}{\small\displaystyle\frac{a^{2}x{\tiny 2}{\small\,+\,}aby{\tiny 2}{\small\,+\,}ac}{a^{2}{\small\,+\,}b^{2}}}\)\(\hspace{10pt}{\small\Rightarrow}\hspace{10pt}\)\(x{\small\;=\;}{\small\displaystyle\frac{a(ax{\tiny 2}{\small\,+\,}by{\tiny 2}{\small\,+\,}c)}{a^{2}{\small\,+\,}b^{2}}}\)

 垂直線 \({\color{#C0C0C0}y{\small\;=\;}{\small-\displaystyle\frac{b}{a}}x}\) を \({\color{#C0C0C0}x{\small\;=\;}{\small-\displaystyle\frac{a}{b}}y}\) に式変形して直線\(\color{#C0C0C0}l^{\prime}\) の式の変数\(x\) に代入する。
\(\color{#C0C0C0}a(x{\small\,-\,}x{\tiny 2}){\small\,-\,}b(y{\small\,+\,}y{\tiny 2}){\small\,-\,}c{\small\,=\,}0\)\(\hspace{10pt}{\small\Rightarrow}\hspace{10pt}\)\(\color{#C0C0C0}a({{\small-\displaystyle\frac{a}{b}}y}{\small\,-\,}x{\tiny 2}){\small\,-\,}b(y{\small\,+\,}y{\tiny 2}){\small\,-\,}c{\small\,=\,}0\)\(\hspace{10pt}{\small\Rightarrow}\hspace{10pt}\)\(\)\(\color{#C0C0C0}{\small-\displaystyle\frac{a^{2}}{b}}y{\small\,-\,}ax{\tiny 2}{\small\,-\,}by{\small\,-\,}by{\tiny 2}{\small\,-\,}c{\small\,=\,}0\)\(\hspace{10pt}{\small\Rightarrow}\hspace{10pt}\)\(\)\(\color{#C0C0C0}{\small -}a^{2}y{\small\,-\,}abx{\tiny 2}{\small\,-\,}{{\small{b^{2}}}y}{\small\,-\,}b^{2}y{\tiny 2}{\small\,-\,}bc{\small\,=\,}0\)\(\hspace{10pt}{\small\Rightarrow}\hspace{10pt}\)\(\color{#C0C0C0}{\small -}(a^{2}{\small +}b^{2})y{\small\,-\,}abx{\tiny 2}{\small\,-\,}b^{2}y{\tiny 2}{\small\,-\,}bc{\small\,=\,}0\)\(\hspace{10pt}{\small\Rightarrow}\hspace{10pt}\)\(\color{#C0C0C0}{\small\,-\,}abx{\tiny 2}{\small\,-\,}b^{2}y{\tiny 2}{\small\,-\,}bc{\small\,=\,}(a^{2}{\small\,+\,}b^{2})y\)\(\hspace{10pt}{\small\Rightarrow}\hspace{10pt}\)\(\color{#C0C0C0}y{\small\;=\;}{\small\displaystyle\frac{{\small -}b^{2}y{\tiny 2}{\small\,-\,}abx{\tiny 2}{\small\,-\,}bc}{a^{2}{\small\,+\,}b^{2}}}\)\(\hspace{10pt}{\small\Rightarrow}\hspace{10pt}\)\(y{\small\;=\;}{\small\displaystyle\frac{{\small -}b(ax{\tiny 2}{\small\,+\,}by{\tiny 2}{\small\,+\,}c)}{a^{2}{\small\,+\,}b^{2}}}\)

 点\(\color{#C0C0C0}\boldsymbol h\) の座標は \(\left({\small\displaystyle\frac{a(ax{\tiny 2}{\small\,+\,}by{\tiny 2}{\small\,+\,}c)}{a^{2}{\small\,+\,}b^{2}}},\,{\small\displaystyle\frac{{\small -}b(ax{\tiny 2}{\small\,+\,}by{\tiny 2}{\small\,+\,}c)}{a^{2}{\small\,+\,}b^{2}}}\right)\) となる。

 それで\(\overline{{\large o}{\color{#C0C0C0}h}}\)\((\)つまり、 \(d\)\()\) を求める。

\({\large d}^{\,2}{\small\;=\;}\)\(\sqrt{\left\{{\small\displaystyle\frac{a(ax{\tiny 2}{\small\,+\,}by{\tiny 2}{\small\,+\,}c)}{a^{2}{\small\,+\,}b^{2}}}\right\}^{2}{\small\;+\;}\left\{{\small\displaystyle\frac{{\small -}b(ax{\tiny 2}{\small\,+\,}by{\tiny 2}{\small\,+\,}c)}{a^{2}{\small\,+\,}b^{2}}}\right\}^{2}}\)\({\small\;=\;}\)\(\sqrt{\left\{{\small\displaystyle\frac{a(ax{\tiny 2}{\small\,+\,}by{\tiny 2}{\small\,+\,}c)}{a^{2}{\small\,+\,}b^{2}}}\right\}^{2}{\small\;+\;}\left\{{\small\displaystyle\frac{{\small -}b(ax{\tiny 2}{\small\,+\,}by{\tiny 2}{\small\,+\,}c)}{a^{2}{\small\,+\,}b^{2}}}\right\}^{2}}\)

\({\small\;=\;}\)\(\sqrt{{\small\displaystyle\frac{a^{2}(ax{\tiny 2}{\small\,+\,}by{\tiny 2}{\small\,+\,}c)^{2}}{(a^{2}{\small\,+\,}b^{2})^{2}}}{\small\;+\;}{\small\displaystyle\frac{\small({\small -}b)^{2} (ax{\tiny 2}{\small\,+\,}by{\tiny 2}{\small\,+\,}c)^{2}}{(a^{2}{\small\,+\,}b^{2})^{2}}}}\)\({\small\;=\;}\)\(\sqrt{\small\displaystyle\frac{(a^{2}{\small\,+\,}b^{2})(ax{\tiny 2}{\small\,+\,}by{\tiny 2}{\small\,+\,}c)^{2}}{(a^{2}{\small\,+\,}b^{2})^{2}}}\)

 \(d{\small\;=\;}\)\({\small\displaystyle\frac{|ax{\tiny 2}{\small\,+\,}by{\tiny 2}{\small\,+\,}c|}{\sqrt{a^{2}{\small\,+\,}b^{2}}}}\) となる。それで、\((x{\tiny 2},\,y{\tiny 2})\) の座標点は 原点\({\Large o}({\small 0},\,{\small 0})\) に移動したので、\(x,y\) 座標を分子の絶対値記号がついた式 \(ax{\tiny 2}{\small\,+\,}by{\tiny 2}{\small\,+\,}c\) の変数\(x{\tiny 2}\)、\(y{\tiny 2}\)に代入すれば \({\small\displaystyle\frac{|\,c\,|}{\sqrt{a^{\tiny 2}{\scriptsize\,+\,} b^{\tiny 2}}}}\) になる。

直線のベクトル方程式

定点\(A\)を通る直線のベクトル方程式 \(\hspace{10pt}\overset{\LARGE\vec{\tiny \,}}{p}{\scriptsize\,=\,}t{\boldsymbol d}{\scriptsize\,+\,}\overset{\LARGE\vec{\tiny \,}}{a}\)

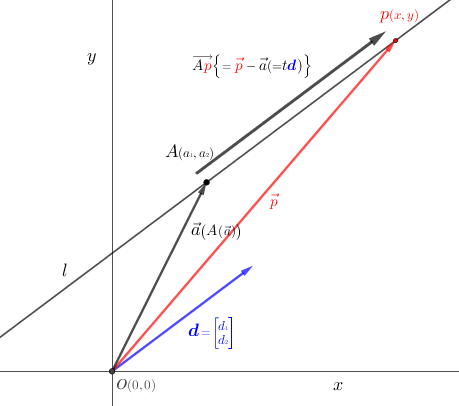
\(\textsf{図$5$から}\left\{\begin{array}{l}\textsf{定点$A$を通る直線を$l$とする。} \\[10pt] \textsf{直線$l$上を移動する動点を$p$とする。座標成分は直線$l$上のすべての点なので、 $(x,y)$ と置く。} \\[10pt] \\ \textsf{定点$A$の位置ベクトル$\overset{\Huge\vec{\tiny}}{\small {\large o}A}{\scriptsize\,=\,}\vec{a}{\scriptsize\,=\,}A{\scriptsize(\vec{a})}$。}\hspace{30pt}\left\{\small\textsf{基準点$\normalsize o$(図$3$では$(0,0)$の原点)から定点$A$までのベクトルを位置ベクトルと定義して$A{\scriptsize(\vec{a})}$と表記する。$\hspace{10pt}$☜$\hspace{5pt}\href{https://showanojoe.com/template-math/linear-algebra/position-vector/}{\textsf{位置ベクトル}}$}\right\} \\[10pt] \textsf{${\Large o}\color{red}{p}{\scriptsize\,=\,}\vec{\color{red}p}$}\hspace{30pt}\left\{\small\textsf{基準点$\normalsize o$から動点$\color{red}p$までのベクトルは$\color{red}{\vec{p}}$。位置ベクトルは定義できない。}\right\} \\[10pt] \textsf{${\color{blue}\boldsymbol d}$ は (直線$l$の)$\class{Boldfont}{\textsf{方向ベクトル}}$、$t$ は $\class{Boldfont}{\textsf{媒介変数}}$ を表す。}\hspace{10pt}\left\{\begin{array}{l}\small\textsf{方向ベクトルとは、直線に対して平行するベクトル($\scriptsize\textsf{大きさ、逆向きは問はない}$)で表した直線の傾きである。} \\ \hspace{10pt}\small\textsf{$\href{#2-1}{\textsf{直線の基本形の式}}\,y{\scriptsize\,=\,}{\scriptsize\displaystyle\frac{a}{b}}x{\tiny\,+\,}{\scriptsize\displaystyle\frac{c}{d}}$ では}\left\{\begin{array}{l}\small\textsf{とりあえず$x$に$0$と$1$を代入する。} \\ {\boldsymbol d}{\scriptsize\,=\,} \begin{bmatrix}\hspace{10pt}1\hspace{10pt}{\scriptsize\,-\,}\hspace{0pt}0 \\ \left({\tiny\displaystyle\frac{a}{b}}{\tiny\,+\,}{\tiny\displaystyle\frac{c}{b}}\right){\scriptsize\,-\,}{\tiny\displaystyle\frac{c}{b}}\end{bmatrix} \end{array}\right\} \\ \hspace{10pt}\small\textsf{$\href{#2-1}{\textsf{直線の一般形の式}}\,\small ax{\tiny\,+\,}by{\tiny\,+\,}c{\tiny\,=\,}0$ では}\left\{\begin{array}{l}\small\textsf{法線ベクトル$\boldsymbol n$の成分は $\scriptsize\begin{bmatrix}a \\ b\end{bmatrix}$ である。$\hspace{10pt}$☜$\hspace{5pt}\href{https://showanojoe.com/template-math/linear-algebra/normal-vector-linear-equations/}{\scriptsize\textsf{法線ベクトルと直線の式}}$} \\ \small\textsf{${\boldsymbol d}\cdot{\boldsymbol n}{\scriptsize\,=\,}0$ なので ${\boldsymbol d}{\scriptsize\,=\,}\scriptsize\begin{bmatrix}{\tiny-}b \\ a\end{bmatrix}$}\end{array}\right\} \\ \small\textsf{媒介変数とは、直線の関数(式)$f{\scriptsize (x,y)}{\scriptsize\,=\,}0\hspace{5pt}\rightarrow\hspace{5pt}x{\scriptsize\,=\,}f{\scriptsize (t)},y{\scriptsize\,=\,}f{\scriptsize (t)}$となる変数$x,y$に共通する入れ子の変数$t$をいう。}\end{array}\right\} \\[10pt] \textsf{直線$l$の式は}\hspace{5pt}\left\{\begin{array}{l}\small\textsf{定点$A$を通る直線のベクトル方程式 $\small\overset{\LARGE\vec{\tiny \,}}{p}{\scriptsize\,=\,}t{\boldsymbol d}{\scriptsize\,+\,}\overset{\LARGE\vec{\tiny \,}}{a}$ に代入して $\small(x,y){\scriptsize\,=\,}t{\scriptsize({\color{blue}{d{\tiny 1}\,d{\tiny 2}}})}{\scriptsize\,+\,}{\scriptsize({\color{red}{a{\tiny 1}\,a{\tiny 2}}})}$} \\ \small{{\scriptsize\hspace{5pt}\rightarrow\hspace{5pt}}x{\scriptsize\,=\,}t{\color{blue}{d{\tiny 1}}}{\scriptsize\,+\,}{\color{red}{a{\tiny 1}}},y{\scriptsize\,=\,}t{\color{blue}{d{\tiny 2}}}{\scriptsize\,+\,}{\color{red}{a{\tiny 2}}}\hspace{20pt}\textsf{これを 媒介変数表示 という。}} \\ \small{t{\scriptsize\,=\,}\displaystyle\frac{x{\tiny\,-\,}\color{red}{a{\tiny 1}}}{\color{blue}d{\tiny 1}}{\scriptsize\,=\,}\displaystyle\frac{y{\tiny\,-\,}\color{red}{a{\tiny 2}}}{\color{blue}d{\tiny 2}}{\scriptsize\hspace{10pt}\rightarrow\hspace{10pt}}t{\scriptsize\,=\,}{\color{blue}d{\tiny 2}}x{\tiny\,-\,}{\color{blue}d{\tiny 2}}{\color{red}{a{\tiny 1}}}{\scriptsize\,=\,}{\color{blue}d{\tiny 1}}y{\tiny\,-\,}{\color{blue}d{\tiny 1}}{\color{red}{a{\tiny 2}}}}\end{array}\right\} \hspace{10pt} {\color{blue}d{\tiny 2}}x{\tiny\,-\,}{\color{blue}d{\tiny 1}}y{\scriptsize\,+\,}{\color{blue}d{\tiny 1}}{\color{red}{a{\tiny 2}}}{\tiny\,-\,}{\color{blue}d{\tiny 2}}{\color{red}{a{\tiny 1}}}{\scriptsize\,=\,}0\end{array}\right.\)

\(2\)点の定点\(A,B\)を通る直線のベクトル方程式\(\hspace{10pt}\overset{\LARGE\vec{\tiny \,}}{p}{\scriptsize\,=\,}({\small 1}{\scriptsize\,-\,}t)\overset{\LARGE\vec{\tiny \,}}{a}{\scriptsize\,+\,}t\Large\vec{\normalsize b}\)

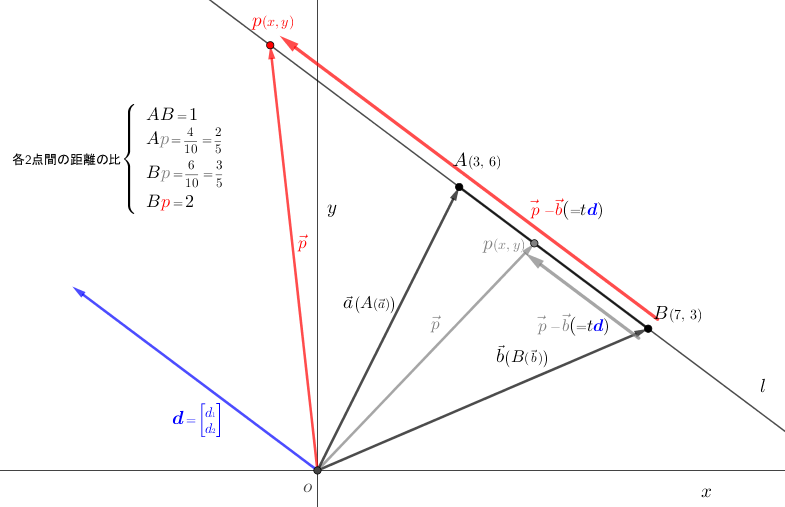
\(\textsf{図$6$から}\left\{\begin{array}{l}\textsf{異なる$2$つの定点$A,B$を通る直線を$l$とする。①直線$l$の式は} \left\{\begin{array}{l}\small\textsf{直線の式 $y{\scriptsize\,=\,}ax{\scriptsize\,+\,}b$ から $A,B{\scriptsize\,=\,}(3,6),(7,3)$ より} \\ {\scriptsize\begin{array}{ccc}&6{\scriptsize\,=\,}3a{\scriptsize\,+\,}b \\[-5pt] {\scriptsize\,-\,}\normalsize{)}\hspace{-5pt}&3{\scriptsize\,=\,}7a{\scriptsize\,+\,}b \\ \hline &3{\scriptsize\,=\,}{\scriptsize\,-\,}4a~\,\end{array}}\hspace{10pt}\rightarrow\hspace{10pt}a{\scriptsize\,=\,}{\scriptsize\,-\,}{\scriptsize\displaystyle\frac{3}{4}},b{\scriptsize\,=\,}{\scriptsize\displaystyle\frac{33}{4}}\end{array}\right\}\hspace{10pt}y{\scriptsize\,=\,}{\scriptsize\,-\,}{\small\displaystyle\frac{3}{4}}x{\scriptsize\,+\,}{\small\displaystyle\frac{33}{4}}\\[10pt] \textsf{直線$l$上を移動する動点を$p$とする。} \\[10pt]\begin{array}{l}{\color{red}\overset{\LARGE\vec{\tiny ~}}{p}}{\scriptsize\,-\,}\Large\vec{\normalsize b}{\scriptsize\,=\,}{{\color{red}{\Large\vec{\normalsize {\color{black}b}p}}}{\scriptsize\,=\,}\normalsize t{\color{blue}{\boldsymbol d}}} \\ {\color{gray}\overset{\LARGE\vec{\tiny ~}}{p}}{\scriptsize\,-\,}\Large\vec{\normalsize b}{\scriptsize\,=\,}{{\color{gray}{\Large\vec{\normalsize {\color{black}b}p}}}{\scriptsize\,=\,}\normalsize t{\color{blue}{\boldsymbol d}}}\end{array} \\[10pt] \textsf{${\color{red}{\overset{\Large\vec{\tiny ~}}{p}}}{\scriptsize\,=\,}{\scriptsize-}\overset{\Large\vec{\tiny ~}}{a}{\scriptsize\,+\,}2\vec{b}$}\hspace{30pt}\left\{\begin{array}{l}\small\textsf{直線$l$におけるベクトル$\color{red}p$の式は${\color{red}\overset{\Large\vec{\tiny ~}}{p}}{\scriptsize\,=\,}{\scriptsize-}\overset{\Large\vec{\tiny ~}}{a}{\scriptsize\,+\,}2\vec{b}$となる。$\left\{\begin{array}{l}\small\textsf{点$\color{red}p$は$\textsf{点$AB$間}$の外側にあるので 外分点 となる。} \\ \small\textsf{外分点の公式は $\scriptsize\displaystyle\frac{{\tiny -}n\overset{\vec{\tiny ~}}{a}{\tiny\,+\,}m\vec{b}}{m{\tiny\,-\,}n}\left(\textsf{線分$ab$を$m:n$に外分する点$\color{red}p$}\right)$ } \\ \small\textsf{外分点は係数の和が $1$ になる性質がある。} \end{array}\right\}$} \\ \small\textsf{ベクトル方程式は $\overset{\LARGE\vec{\tiny \,}}{p}{\scriptsize\,=\,}(1{\scriptsize\,-\,}t )\overset{\LARGE\vec{\tiny \,}}{a}{\scriptsize\,+\,}t\,\Large\vec{\small b}\hspace{5pt}{\scriptsize\rightarrow}\hspace{5pt}\small{\overset{\LARGE\vec{\tiny \,}}{p}{\scriptsize\,=\,}s\,\overset{\LARGE\vec{\tiny \,}}{a}{\scriptsize\,+\,}t\,\Large\vec{\small b}},s{\scriptsize\,+\,}t\,{\scriptsize\,=\,}1(\small\textsf{(${\scriptsize 1}{\tiny\,-\,}t){\tiny\,=\,}s$とする。})$なので単純に外分点の公式に当てはめればいい。}\end{array}\right\} \\[10pt] \textsf{${\color{gray}{\overset{\Large\vec{\tiny ~}}{p}}}{\scriptsize\,=\,}{\scriptsize\displaystyle\frac{3}{5}}\:\overset{\Large\vec{\tiny ~}}{a}{\scriptsize\,+\,}{\scriptsize\displaystyle\frac{2}{5}}\:\vec{b}$}\hspace{30pt}\left\{\begin{array}{l}\small\textsf{直線$l$におけるベクトル$\color{gray}p$の式は${\color{gray}{\overset{\Large\vec{\tiny ~}}{p}}}{\scriptsize\,=\,}{\scriptsize\displaystyle\frac{3}{5}}\:\overset{\Large\vec{\tiny ~}}{a}{\scriptsize\,+\,}{\scriptsize\displaystyle\frac{2}{5}}\:\vec{b}$となる。$\left\{\begin{array}{l}\small\textsf{点$\color{gray}p$は$\textsf{点$AB$間}$の内側にあるので 内分点 となる。} \\ \small\textsf{内分点の公式は $\scriptsize\displaystyle\frac{n\overset{\vec{\tiny ~}}{a}{\tiny\,+\,}m\vec{b}}{m{\tiny\,+\,}n}\left(\textsf{線分$ab$を$m:n$に内分する点$\color{gray}p$}\right)$ } \\ \small\textsf{外分点は係数の和が $1$ になる性質がある。} \end{array}\right\}$} \\ \small\textsf{ベクトル方程式は $\overset{\LARGE\vec{\tiny \,}}{p}{\scriptsize\,=\,}(1{\scriptsize\,-\,}t )\overset{\LARGE\vec{\tiny \,}}{a}{\scriptsize\,+\,}t\,\Large\vec{\small b}\hspace{5pt}{\scriptsize\rightarrow}\hspace{5pt}\small{\overset{\LARGE\vec{\tiny \,}}{p}{\scriptsize\,=\,}s\,\overset{\LARGE\vec{\tiny \,}}{a}{\scriptsize\,+\,}t\,\Large\vec{\small b}},s{\scriptsize\,+\,}t\,{\scriptsize\,=\,}1(\small\textsf{(${\scriptsize 1}{\tiny\,-\,}t){\tiny\,=\,}s$とする。})$なので単純に内分点の公式に当てはめればいい。}\end{array}\right\} \\[10pt] \textsf{②直線$l$の式は}\hspace{5pt}\left\{\begin{array}{l}\small\textsf{$2$点の定点$A,B$を通る直線のベクトル方程式 $\small\overset{\LARGE\vec{\tiny \,}}{p}{\scriptsize\,=\,}(1{\scriptsize\,-\,}t)\overset{\LARGE\vec{\tiny \,}}{a}{\scriptsize\,+\,}t\,\Large\vec{\small b}$ に代入して $\small(x,y){\scriptsize\,=\,}{\scriptsize(1{\scriptsize\,-\,}t)}{\scriptsize(3,6)}{\scriptsize\,+\,}t{\scriptsize(7,3)}$} \\ \small{{\scriptsize\hspace{5pt}\rightarrow\hspace{5pt}}x{\scriptsize\,=\,}3(1{\scriptsize\,-\,}t){\scriptsize\,+\,}7t,y{\scriptsize\,=\,}6(1{\scriptsize\,-\,}t){\scriptsize\,+\,}3t{\scriptsize\hspace{5pt}\rightarrow\hspace{5pt}}x{\scriptsize\,=\,}3{\scriptsize\,+\,}4t,y{\scriptsize\,=\,}6{\scriptsize\,-\,}3t} \\ \small{t{\scriptsize\,=\,}\displaystyle\frac{x{\tiny\,-\,}3}{4}{\scriptsize\,=\,}\displaystyle\frac{y{\tiny\,-\,}6}{{\scriptsize\,-\,}3}{\scriptsize\hspace{10pt}\rightarrow\hspace{10pt}}t{\scriptsize\,=\,}{\scriptsize\,-\,}3x{\tiny\,+\,}9{\scriptsize\,=\,}4y{\tiny\,-\,}24}\end{array}\right\} \hspace{10pt}y{\scriptsize\,=\,}{\scriptsize\,-\,}{\small\displaystyle\frac{3}{4}}x{\scriptsize\,+\,}{\small\displaystyle\frac{33}{4}} \\[10pt] \textsf{①と②の式は同じ式となる。}\end{array}\right.\)

ベクトル \(\vec{n}\) に垂直な定点\(A\)を通る直線のベクトル方程式\(\hspace{10pt}{\boldsymbol n}\cdot\vec{p}{\scriptsize\,-\,}\vec{a}{\scriptsize\,=\,}0\)

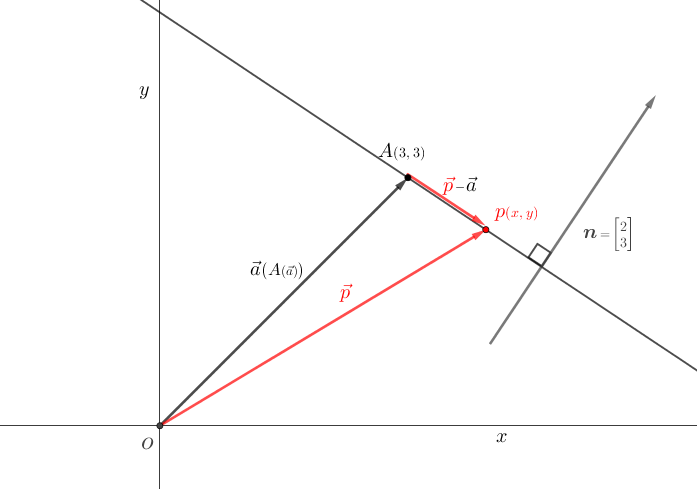
\(\textsf{図$7$から}\left\{\begin{array}{l}\textsf{${\color{red}\vec{p}}{\scriptsize\,-\,}\vec{a}$ の座標成分は $(x{\scriptsize\,-\,}3,y{\scriptsize\,-\,}3)$} \\[10pt] \textsf{ベクトル${n}$に垂直な定点\(A\)を通る直線のベクトル方程式$\hspace{10pt}{\boldsymbol n}\cdot\vec{p}{\scriptsize\,-\,}\vec{a}{\scriptsize\,=\,}0$ から直線$l$の式は $2(x{\scriptsize\,-\,}3){\scriptsize\,+\,}3(y{\scriptsize\,-\,}3){\scriptsize\,=\,}0$} \\[10pt] \textsf{いずれにせよ、$2$つの $\href{https://showanojoe.com/template-math/linear-algebra/dot-product-of-vectors/#1}{\textsf{ベクトルの直交}}$ は その内積が$0$ である。}\end{array}\right.\)