単純パーセプトロンのパラメータ\(\{b(w {\tiny 0}),\,w{\tiny 1},\,w{\tiny 2}\}\) の調整だけでは処理できない(線形分離できない)場合は層を重ね合わせた 多層パーセプトロン で出力を調整する\((\textsf{単純パーセプトロンの限界})\)。
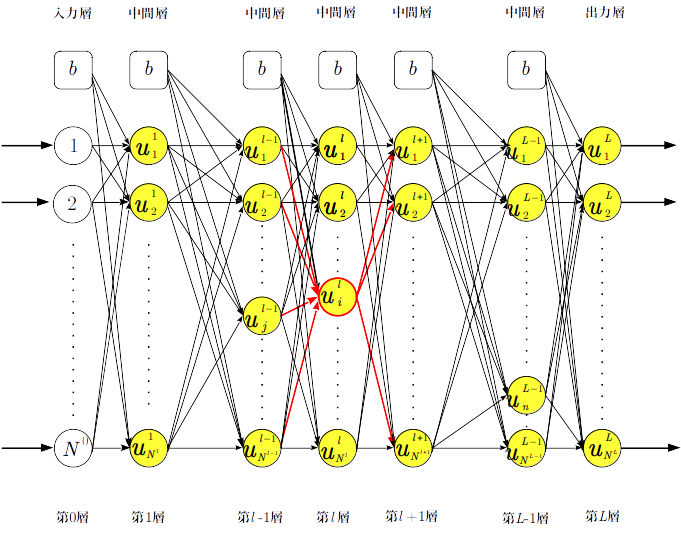
\(\textsf{図$3$から}\left\{\begin{array}{l}\textsf{各ユニット(黄色に塗りつぶした円)はそれぞれ単純パーセプトロンの動作をする。} \\ \textsf{ここでは入力層を第\(0\)層とし、出力層までを\(L\)層、各層のバイアス\(b\)を除いたユニットの個数$(\small\textsf{入力層はノードの個数})$を} \\ \hspace{10pt}\textsf{\(N\)として入力\(x\)、重み\(w\)、出力\(o(\small\textsf{ユニットからユニットへの出力})\)、ユニット\(u\)にかかる上下添字を定義してそれぞれを} \\ \hspace{10pt}\textsf{配置した。上添字は層の順$(\textsf{番号})$、下添字は層内のユニットの個数$N$に上添字の層の順$(\textsf{番号})$。重み$w$の場合は層内のユニットとその} \\ \hspace{10pt}\textsf{一つ前のユニットの順$(\textsf{番号})$。}\end{array}\right.\)
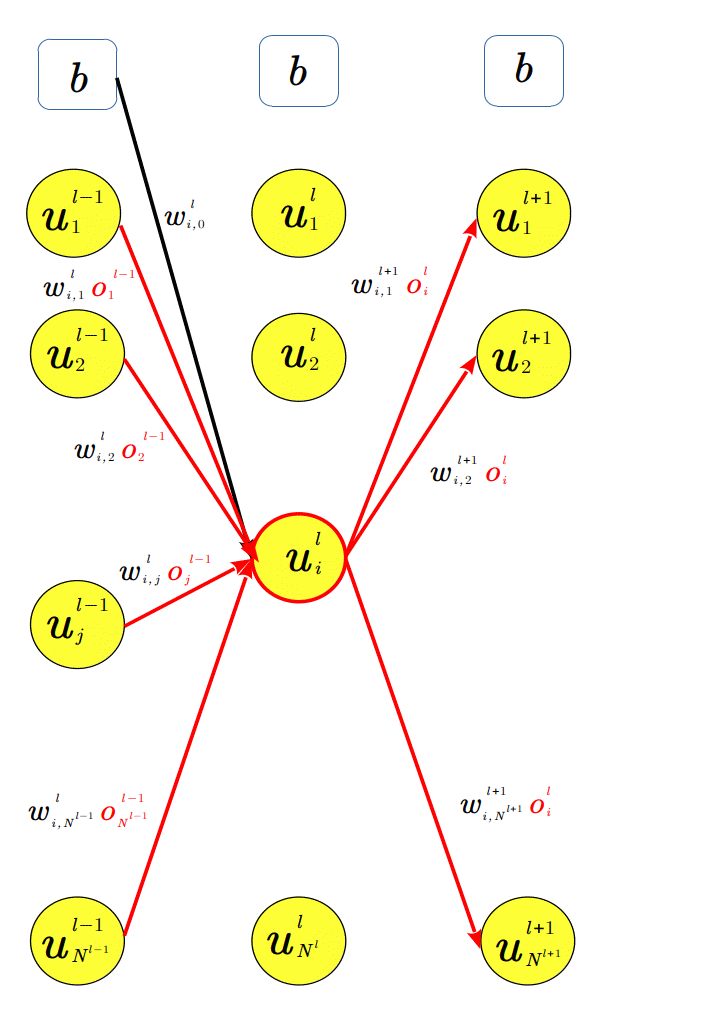
\(\textsf{図$4$から}\left\{\begin{array}{l}\textsf{ユニット$u\overset{\tiny l}{\tiny i}$の線形識別関数式}\hspace{5pt}{\Large o}\overset{\,\scriptsize l}{\,\scriptsize i}{\scriptsize\:=\:}{h}{\small ({u}\overset{\,\tiny l}{\,\tiny i})} \\ \hspace{10pt}{u}\overset{\,\tiny l}{\,\tiny i}{\scriptsize\:=\:}{\begin{eqnarray}\sum_{\scriptsize{k=0}}^{\scriptsize{N^{l-1}}}\end{eqnarray}\,{w}\!\overset{\,\tiny l}{\,\tiny i,k}\,o\overset{\tiny l-1}{\tiny k}}{\scriptsize\:=\:}{w}\!\overset{\,\tiny l}{\,\tiny i,0}{\scriptsize\:+\:}{w}\!\overset{\,\tiny l}{\,\tiny i,1}\,o\overset{\tiny l-1}{\tiny 1}{\scriptsize\:+\:}{w}\!\overset{\,\tiny l}{\,\tiny i,2}\,o\overset{\tiny l-1}{\tiny 2}{\scriptsize\:+\:}\cdots{\scriptsize\:+\:}{w}\!\overset{\,\tiny l}{\,\tiny i,j}\,o\overset{\tiny l-1}{\tiny j}{\scriptsize\:+\:}\cdots{\scriptsize\:+\:}{w}\!\overset{\,\tiny l}{\,\tiny i,N^{l-1}}\,o\overset{\tiny l-1}{\tiny N^{l-1}}\end{array}\right.\)
ちなみに図1,3,4のような図形を データフローグラフ という。

