\(2\)次関数
\(2\)次関数は、変数 \(x\) の\(2\)次\((x^2)\)式で表す関数である。
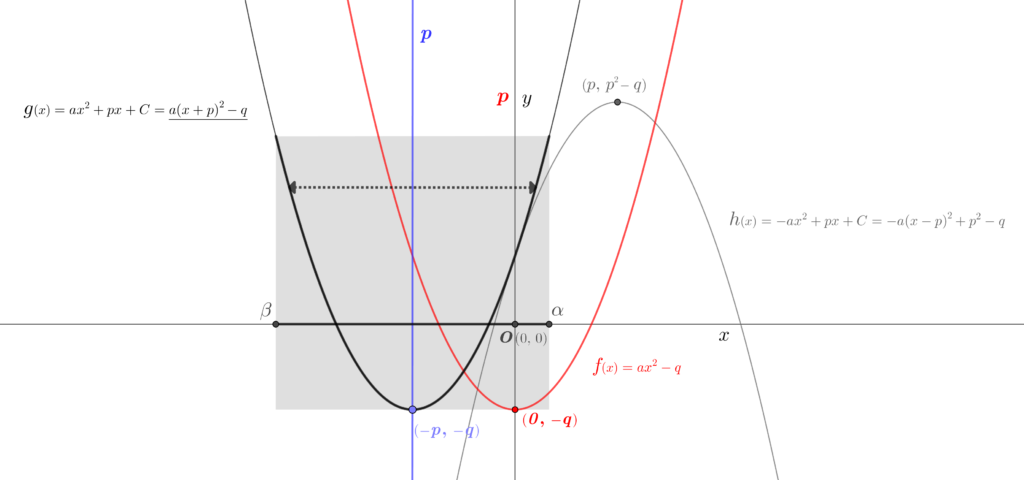
図\(1\)から、\(\color{red}{\large f}{\small (x)}{\small\,=\,}ax^{2}-q\) は、軸\((\textsf{グラフが対称となる線})\)が\(y\)の座標軸 \(\color{red}p\)、下に凸である頂点は\(\color{red}(0,\,{\small-}q)\) の \(2\)次関数のグラフである。これを基準に、
\(x\)座標を \(\color{blue}{\small -}p\) 平行移動したグラフは軸が \(\color{blue}p\)、頂点が \(\color{blue}({\small -}p,\,{\small -}q)\) の\(2\)次関数 \(a(x+p)^{2}\!-q\) のグラフになる。この\(2\)次関数 \(\large g{\small(x)}\) の係数\(a\) の符号を \(-\) にすると上に凸の \(\color{gray}\large h{\small(x)}\) のグラフになる。
\(2\)次関数のグラフの軸と頂点は、 因数分解 をもとに 平方完成 した変形式 \(a(x+p)^{2}\!-q\) にすると求めやすい。\(\large g{\small(x)}\) では \(ax^{2}{\small\,+\,}bx{\small\,+\,}C\)を平方完成した \(ax^{2}{\small\,+\,}bx{\small\,+\,}C\) の式になる。
\(\color{gray}\textsf{事例}\)\(\hspace{20pt}\)\(2\)次関数 \({\small\displaystyle\frac{1}{5}}x^{2}{\small\,+\,}3x{\small\,+\,}2\) のグラフの軸と頂点を求めてみる。
まずは、\(ax^2+bx+C\) の\(2\)次関数の定義式に沿って、\(1\)次数\(x\)の係数\(b\)から、軸と頂点を求める 平方完成 の定義式 \(a(x-p)^{2}+q\) の \(p\) を求める。
与式 \({\small\displaystyle\frac{1}{5}}x^{2}{\small\,+\,}3x{\small\,+\,}2\) の\(1\)次数\(x\)の係数\(b\)は 符号\({\small +}3\) なので、 \(a(x-p)^{2}+q\) の \(p\) は \(3{\small\,=\,}{\small\displaystyle\frac{1}{5}}\cdot2\cdot {\small -}p\) より \(p{\small\,=\,}{\small-\displaystyle\frac{15}{2}}\) になる。
それで、\({\small\displaystyle\frac{1}{5}}\)\(\left\{x-(-{\small\displaystyle\frac{15}{2}})\right\}^{2}\)\({\small\,=\,}{\small\displaystyle\frac{1}{5}}x^{2}\)\({\small\,+\,}3x{\small\,+\,}{\small\displaystyle\frac{45}{4}}\)、 与式の \(C\) は \(2\) なので、\(2{\small\,=\,}{\small\displaystyle\frac{45}{4}}{\small\,+\,}q\)\({\small\hspace{5pt}\rightarrow\hspace{5pt}}\)\(q{\small\,=\,}{\small-\displaystyle\frac{37}{4}}\)。
よって、事例の\(2\)次関数のグラフは\({\small\displaystyle\frac{1}{5}}\)\(\left\{x-(-{\small\displaystyle\frac{15}{2}})\right\}^{2}{\small\,+\,}({\small-\displaystyle\frac{37}{4}})\) の式変形により、軸が \({\small-\displaystyle\frac{15}{2}}\)、頂点が \(({\small-\displaystyle\frac{15}{2}},\,{\small-\displaystyle\frac{37}{4}})\) となる。
\(x\)軸の範囲\(\alpha\sim\beta\)を設ける\((\textsf{定義域という})\)と、グラフの範囲\((\textsf{値域という})\)はその領域\((\textsf{グレーの塗りつぶし部分})\)内に限定される。もっとも定義域、値域は\(2\)次関数のグラフに限ったことではないが。
ちなみに、\(\large g{\small(x)}\)の破線の線分は係数\(a\)が\(0\)に近いほどグラフの放物線の幅が広く、遠いほど狭くなることの表現を意図した。係数\(a\)とこの関係は\(2\)次関数のグラフ全てにいえることである。
平方完成とは、以下に解説する。
平方完成とは、平面における関数、方程式の\(2\)次式を\(1\)次式の\(2\)乗\((\)平方\()\)の式に式変形することである。
\(2\)次の定義式 \(ax^{\small 2}{\small\;+\;}bx{\small\;+\;}c\) を平方完成の定義式 \(a(x{\small\,-\,}p)^{\small 2}{\small\;+\;}q\) に変形して式を完成させる。
事例は上述の計算メモに記した与式 \({\small\displaystyle\frac{1}{5}}x^{2}{\small\,+\,}3x{\small\,+\,}2\) に譲る。
偶関数 奇関数
偶関数と奇関数は\(\href{https://showanojoe.com/template-math/integral/#定積分}{\textsf{定積分}}\)の単元である。
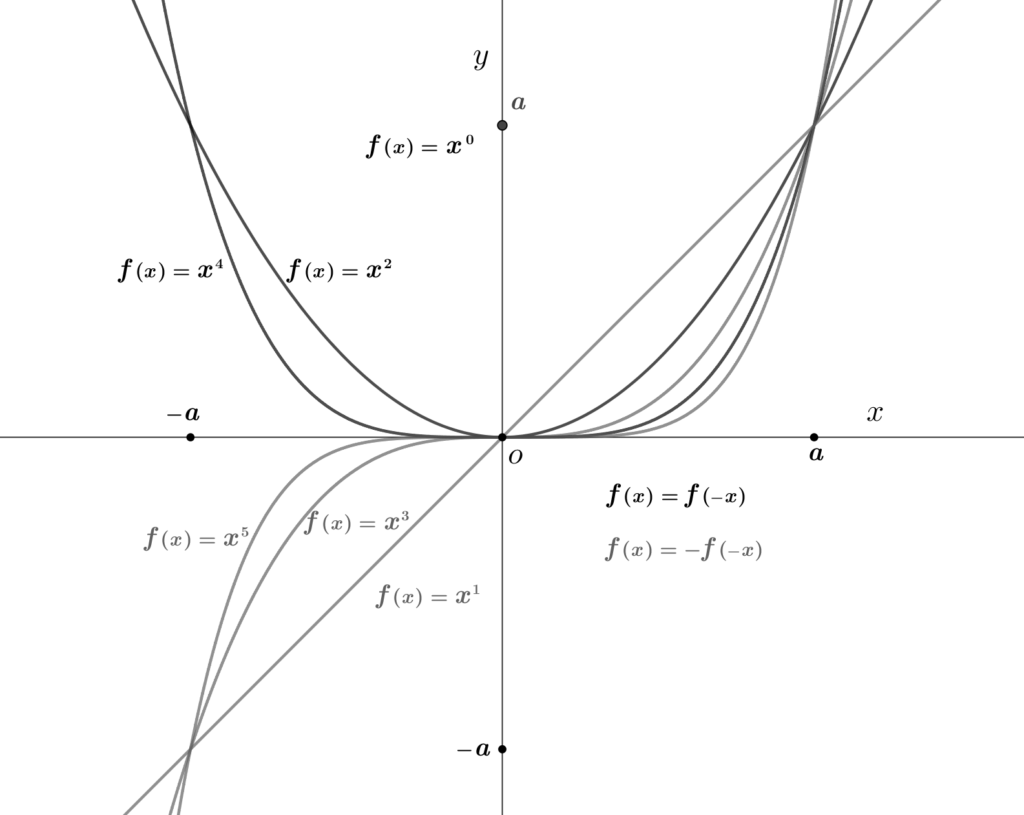
偶関数は \({\large f}{\small (x)}{\small\,=\,}{\large f}{\small (-x)}\) を満たす関数である。図\(1\)の \(x\) の次数が偶数であり、\(y\) の座標軸に対称なグラフになる。
偶関数の定積分\(\hspace{10pt}\)\({\small\displaystyle\int_{\color{red}{\scriptsize -}a}^{\color{red}a}}f{\tiny(x)}\,{\small dx}\)\({\small\;\hspace{5pt}=\;}2{\small\displaystyle\int_{0}^{a}}f{\scriptsize(x)}\,{\small dx}\)
\(\{\)積分区間は符号\(({\small +,\,-})\)が違う同じ真数\((\)ここでは \(\color{red}\large a\)\()\)であることが条件。\(\}\)
奇関数は \(\color{gray}{\large f}{\small (x)}{\small\,=\,}{\small -}{\large f}{\small (-x)}\) を満たす関数である。 \(x\) の次数が奇数であり、\(x,\,y\) の座標軸の交点\((\)原点\(\large o\)\()\)に対称なグラフになる。
奇関数の定積分\(\hspace{10pt}\)\({\small\displaystyle\int_{\color{red}{\scriptsize -}a}^{\color{red}a}}{\color{gray}f{\tiny(x)}}\,{\small dx}\)\({\small\;\hspace{5pt}=\;}0\)
\(\{\)積分区間は符号\(({\small +,\,-})\)が違う同じ真数\((\)ここでは \(\color{red}\large a\)\()\)であることが条件。\(\}\)
\(\color{gray}{\textsf{[事例]}}\)
\({\small\displaystyle\int_{{\tiny}\pi}^{\pi}}{\small cos}x{\small\:-\:sin}x\,{\small dx}\)
