$2$次曲線の方程式

放物線の定義と方程式
楕円の定義と方程式

放物線の定義と方程式

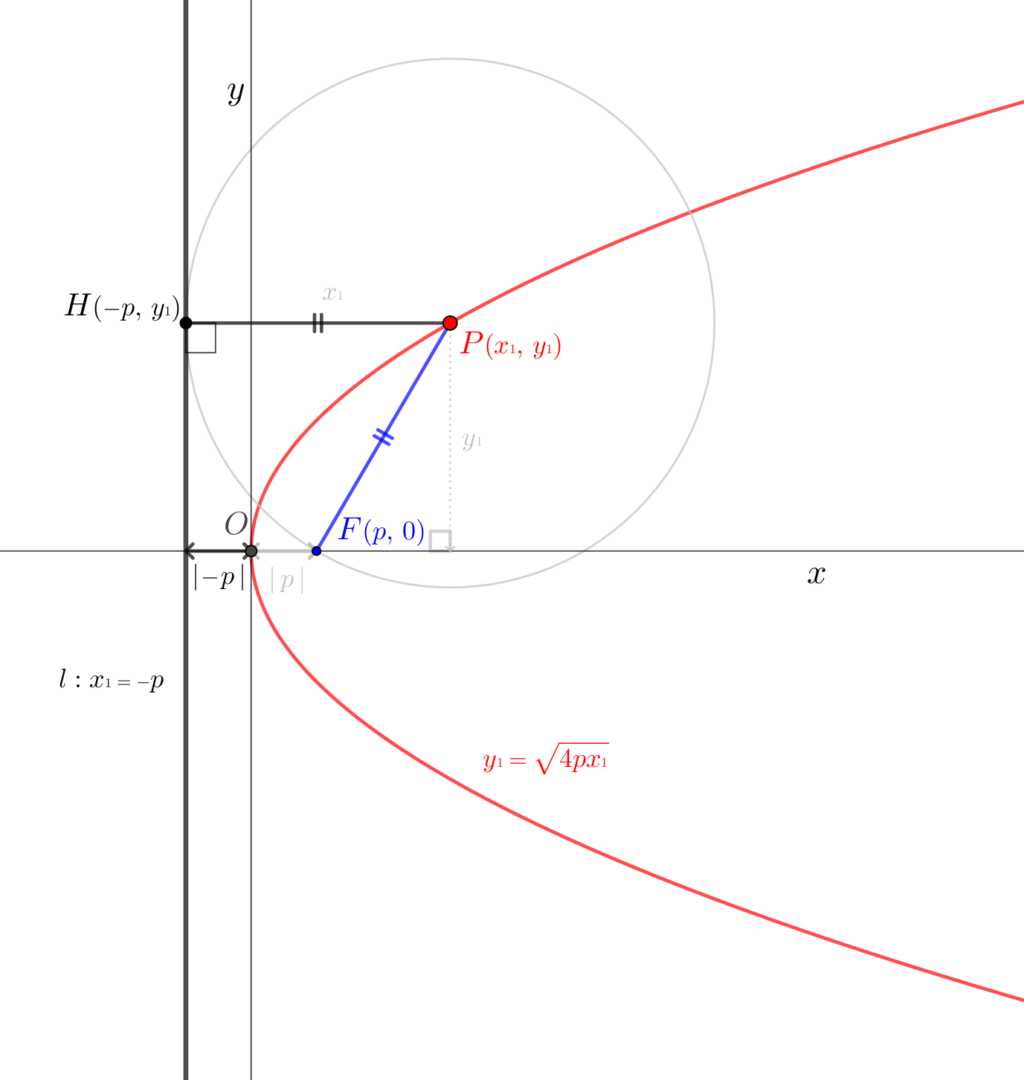
上図 $1$ から、放物線とは、直線 $l$ $($ 準線という $)$ と、その上にない任意の一点 $P$ を中心点とする円周上の点 $F$ をとるとき $($ ただし $H$ $\neq$ $F$ 。点 $H$ は点 $P$ から $l$ に垂線をおろした交点。 $)$ 、 $P$ から焦点 $F$ への距離 $\overset{―}{P F}$ と等しい距離 $\overset{―}{P H}$ を持つような準線 $l$ 上の点 $H$ が存在するようなものの軌跡として定義される平面曲線である。

赤い曲線 $($ つまり放物線 $)$ を軌道とする点を $P (x 1, y 1)$ 、焦点を $F (p, 0)$ 、準線 $l$ の式を $y 1 = - p$ とすると、
上図の放物線の定義式は $\overset{―}{P F} = \overset{―}{P H}$ より
$\sqrt{(x 1 - p)^{2} + y 1^{2}}$ $= | x 1 - (- p) |$ $\Rightarrow$ $(x 1 - p)^{2} + y 1^{2}$ $= x 1^{2} + 2 x 1 y 1 + y 1^{2}$ $\Rightarrow$ $y 1^{2} = 4 p x 1$ $\Rightarrow$ $y 1 = \sqrt{4 p x 1}$
となる $($ 以下で解説 $)$ 。

解説メモ

$\overset{―}{P F}$ の式 $\sqrt{(x 1 - p)^{2} + y 1^{2}}$ は三角関数から、 $三平方の定理$ を用いた $2$ 点 $P$ 、 $F$ 間の距離による。
$\overset{―}{P H}$ は $点と直線の距離$ から公式 $d$ $($ $2$ 点間の距離を表す記号 $)$ $=$ $\frac{| a x 2 + b y 2 + c |}{\sqrt{a^{2} + b^{2}}}$ に準線 $l$ の式 $| x 1 = - p |$ を直線の式の一般形に変形した $x 1 + p = 0$ の左辺の項を代入した式 $\frac{| 1 x 2 + 0 y 2 - (- p) |}{\sqrt{1^{2} + 0^{2}}}$ $\Rightarrow$ $| x 1 = - (- p) |$ 。

放物線の定義と方程式

楕円の定義と方程式