定積分から\(2\)重積分へ
\(S{\small\,=\,}\displaystyle\int_{\alpha}^{\beta}\!{\large f}{\small(x)}\,dx\)\(\hspace{10pt}\Rightarrow\hspace{10pt}V{\small\,=\,}\displaystyle\int \!\!\!\int_D {\large f}{\small(x,\,y)}\,dydx\hspace{10pt}D{\small\,=\,}(x,\,y)\)
定積分は平面のある区間\(\scriptsize(\textsf{$\alpha\sim\beta$})\)の面積\((S)\)であり、\(2\)重積分は立体のある領域\((D)\)の体積\((V)\)である。
\(2\)重積分\((\)体積\()\)の導出
\(\color{gray}{\textsf{[事例]}}\)
\(\small\displaystyle\int\!\!\!\int_D xy\,dxdy\hspace{10pt}D{\scriptsize\,=\,}(y\,|\,{\scriptsize\displaystyle\frac{1}{2}}x^{2}{\scriptsize +}1\:{\scriptsize \leqq}\:y\:{\scriptsize \leqq}\:{\scriptsize -}x{\scriptsize +}3)\)
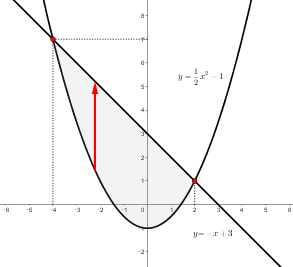
事例では、\(x\) の領域が指定されていないので、\(y{\small\,=\,}{\scriptsize\displaystyle\frac{1}{2}}x^{2}{\small\,+\,}1,\,y{\small\,=\,}{\small\,-}x{\small\,+\,}3\) のグラフを図示して \(x\) の領域を求める必要がある。
図示した図\(1\)から、\(x\) の領域は\({\scriptsize -}4\:{\scriptsize \leqq}\:x\:{\scriptsize \leqq}\:2\) となった。課題は二つの関数グラフに挟まれた着色部分である。これは導出する体積の底面積になる。\(y\) の領域が \(x\) の関数\(\left\{f{\small(x)}{\scriptsize\,=\,}{\scriptsize\displaystyle\frac{1}{2}}x^{2}{\scriptsize +}1,\,f{\small(x)}{\scriptsize \,=\,-}x{\scriptsize +}3\right\}\)にはさまれているので、この領域は 縦線領域 となる。赤い矢印はこの事例の領域が縦線領域であることを示している。\(\small\displaystyle\int\!\!\!\int_D xy\,dxdy\hspace{10pt}D{\scriptsize\,=\,}(x,\,y\,|\:{\scriptsize -}4\:{\scriptsize \leqq}\:x\:{\scriptsize \leqq}\:2,\,{\scriptsize\displaystyle\frac{1}{2}}x^{2}{\scriptsize +}1\:{\scriptsize \leqq}\:y\:{\scriptsize \leqq}\:{\scriptsize -}x{\scriptsize +}3)\)\({\scriptsize\,=\,}\small\displaystyle\int\!\!\!\int_D xy\,dxdy\hspace{5pt}{\scriptsize\,=>\,}\small\displaystyle\int_{{\tiny -}4}^2\fcolorbox{gray}{#fff}{$\!\!\int_{\tiny\displaystyle\frac{1}{2}x^{2}+1}^{\scriptsize -x+3} xy\,dy\!$}dx \)\(D\) が縦線領域なので \(dy\) を先に処理する。重積分はここから 累次積分 で導出していく。\({\scriptsize\,=\,}\hspace{5pt}\small\displaystyle\int_{{\tiny -}4}^2\left[{\scriptsize\displaystyle\frac{xy^{2}}{2}}\right]_{\tiny\displaystyle\frac{1}{2}x^{2}+1}^{\scriptsize -x+3} dx\hspace{5pt}{\scriptsize\,=\,}\hspace{5pt}{\color{red}\underline{\color{black}\small\displaystyle\int_{{\tiny -}4}^2\left[{\scriptsize\displaystyle\frac{1}{2}}\cdot xy^{2}\right]_{\tiny\displaystyle\frac{1}{2}x^{2}+1}^{\scriptsize -x+3} dx}}\)\(\hspace{5pt}{\scriptsize\,=\,}\hspace{5pt}{\scriptsize\displaystyle\frac{1}{2}}\small\displaystyle\int_{{\tiny -}4}^2 x({\scriptsize -}x{\scriptsize +}3)^{2}-x\left({\scriptsize\displaystyle\frac{1}{2}}x^{2}{\scriptsize\,+\,}1\right)^{2}\, dx\)
累次積分の過程において、中辺の式の段階で区間の上下端 \({\scriptsize -}x{\scriptsize +}3,\,{\scriptsize\displaystyle\frac{1}{2}}x^{2}{\scriptsize +}1\) を \(y\) に代入する。\({\scriptsize\,=\,}\hspace{5pt}{\scriptsize\displaystyle\frac{1}{2}}\small\displaystyle\int_{{\tiny -}4}^2 x(x^{2}{\scriptsize -}6x{\scriptsize +}9)-x\left({\scriptsize\displaystyle\frac{1}{4}}x^{4}{\scriptsize\,+\,}x^{2}{\scriptsize\,+\,}1\right)\, dx\)\(\hspace{5pt}{\scriptsize\,=\,}\hspace{5pt}{\scriptsize\displaystyle\frac{1}{2}}\small\displaystyle\int_{{\tiny -}4}^2-{\scriptsize\displaystyle\frac{1}{4}}x^{5}{\scriptsize -}6x^{2}{\scriptsize\,+\,}8x\, dx\)\(\hspace{5pt}{\scriptsize\,=\,}\hspace{5pt}{\small\displaystyle\frac{1}{2}}\left[-{\scriptsize\displaystyle\frac{1}{4}}\cdot {\scriptsize\displaystyle\frac{x^{6}}{6}}\hspace{5pt}{\scriptsize -}6\cdot {\scriptsize\displaystyle\frac{x^{3}}{3}}\hspace{5pt}{\scriptsize\,+\,}8\cdot{\scriptsize\displaystyle\frac{x^{2}}{2}}\right]_{{\tiny -}4}^{\,2}\)
あとは平計算で答えが出る。
\(\color{gray}\textsf{[事例$2$]}\)
\(\small\displaystyle\int\!\!\!\int_D -3e^{-y^{2}}\,dxdy\hspace{10pt}D{\scriptsize\,=\,}(x,\,y\,|\,0\:{\scriptsize \leqq}\:x\:{\scriptsize \leqq}\:1,\,x\:{\scriptsize \leqq}\:y\:{\scriptsize \leqq}\:1)\)
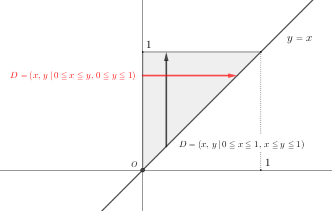
\(\small\displaystyle\int_{0}^{1}\fcolorbox{gray}{#fff}{$\!\!\int_{x}^{1} -3e^{-y^{2}}\,dy$}dx\)\({\normalsize\hspace{5pt}\cdots\hspace{5pt} ?!}\)
縦線領域なので、先に \(\color{gray}\small\boxed{{\phantom {aa}}}\)内の累次積分になるのだが、\(y\) で\(\href{https://showanojoe.com/template-math/limits-and-derivatives/#偏微分}{\color{teal}\textsf{偏微分}}\)する \(-3e^{-y^{2}}\) の\(\href{https://showanojoe.com/template-math/integral/#積分の定義}{\color{teal}\textsf{原始関数}}\)が初等関数では表せない\((\textsf{指数部に $y$ があるので $y$ で積分できない})\)。 そこで、\(y\) の領域が \(x\) の 関数\({\large f}{\small(x)}\) になっている 縦線領域 \(D{\scriptsize\,=\,}(x,\,y\,|\,0\:{\scriptsize \leqq}\:x\:{\scriptsize \leqq}\:1,\,x\:{\scriptsize \leqq}\:y\:{\scriptsize \leqq}\:1)\)\(x\) は \(0\) から \(1\) に移動し、\(y\) は \(f{\scriptsize(y)}{\small\,=\,}x\) から \(1\) に伸びる。} を、 \(x\) の領域が \(y\) の関数\({\large f}{\small(y)}\) になる横線領域 \(\color{red}D{\scriptsize\,=\,}(x,\,y\,|\,0\:{\scriptsize \leqq}\:x\:{\scriptsize \leqq}\:y,\,0\:{\scriptsize \leqq}\:y\:{\scriptsize \leqq}\:1)\)\(x\) は \(0\) から \(f{\scriptsize (x)}{\small\,=\,}y\) に伸び、\(y\) は \(0\) から \(1\) に移動する。} と交換する。右上図\(2\)を参照。
\(\small\displaystyle\int\!\!\!\int_D -3e^{-y^{2}}\,dxdy\)\(\hspace{10pt}D{\scriptsize\,=\,}(x,\,y\,|\,y\:{\scriptsize \leqq}\:x\:{\scriptsize \leqq}\:1,\,0\:{\scriptsize \leqq}\:y\:{\scriptsize \leqq}\:1)\)\({\small\,=>\,}\small\displaystyle\int_{0}^{1}\fcolorbox{gray}{#fff}{$\!\!\int_{0}^{y} -3e^{-y^{2}}$}\,dy\)\({\small\,=\,}\small\displaystyle\int_{0}^{1}\left[-3\cdot xe^{-y^{2}}\right]_{0}^{y}\,dy\,\)\({\small\,=\,}-3\small\displaystyle\int_{0}^{1}ye^{-y^{2}}\,dy\)
\({\small -}3\) を定数倍、\(e^{-y^{2}}\) を定数とし、\(x\) に \(y\) を代入した。\(\overset{y^{2}{\small\,=\,}t}{\small~=>\,}-3{\small\displaystyle\int_{0}^{1}}\sqrt{t}\,({\small -}e^{-t}){\small\displaystyle\frac{1}{2\sqrt{t}}}\cdot dt{\small\,=\,}-3\cdot {\small\displaystyle\frac{1}{2}}\left[{\small -}e^{-t}\right]_{0}^{1}\)\({\small\,=\,}{\small-\displaystyle\frac{3}{2}}({\small-\displaystyle\frac{1}{e^{t}}}{\small -}(-1))\)\({\small\,=\,}{\small\displaystyle\frac{3}{2e^{t}}-\displaystyle\frac{3}{2}}\)
\(y^{2}\) を \(t\) に置換すると \(y{\small\,=\,}\sqrt{t}\) となるので、\(y\) を \(\sqrt{t}\) に変換。\(e^{-t}\) の原始関数\((\textsf{不定積分})\)は \({\small -}e^{-t}\) になる\((\small\textsf{以下証明})\)。\({\scriptsize\displaystyle\int}{\small e^{\scriptsize -t}dt} \left\{\begin{array}{l}\small\textsf{$ -t{\scriptsize\,=\,} u$とおき、${\scriptsize\displaystyle\frac{d}{dt}}({\tiny -}t)\,dt{\scriptsize\,=\,}{\scriptsize\displaystyle\frac{d}{du}}u\,du$ とすると、} \\ \hspace{20pt}\small\textsf{$-1\cdot dt{\scriptsize\,=\,}1\cdot du$ となり、$dt{\scriptsize\,=\,}-du$ ということになる。} \\ \small\textsf{これを、与式 ${\scriptsize\displaystyle\int}{\small e^{\scriptsize -t}dt}$にあてはめてみる。} \\ \small\textsf{${\scriptsize\displaystyle\int}{\small e^{\scriptsize u}({\scriptsize -}du)}{\scriptsize\,=\,}{-\scriptsize\displaystyle\int}{\small e^{\scriptsize u}\,du}{\scriptsize\,=\,}-e^{u}$ したがって、${\scriptsize\displaystyle\int}{\small e^{\scriptsize -t}dt}{\scriptsize\,=\,}-e^{-t}$ となる。} \end{array}\right.\)
\(\color{gray}\textsf{[事例$3$]}\)
\( \small\displaystyle\int\!\!\!\int_D x^{2}\,dxdy\hspace{10pt}D{\scriptsize\,=\,}(x,\,y\,|\,{\color{red}\underline{\color{black} x^{2}{\small\,+\,}y^2\:{\scriptsize \leqq}\:r^{2}}})\)

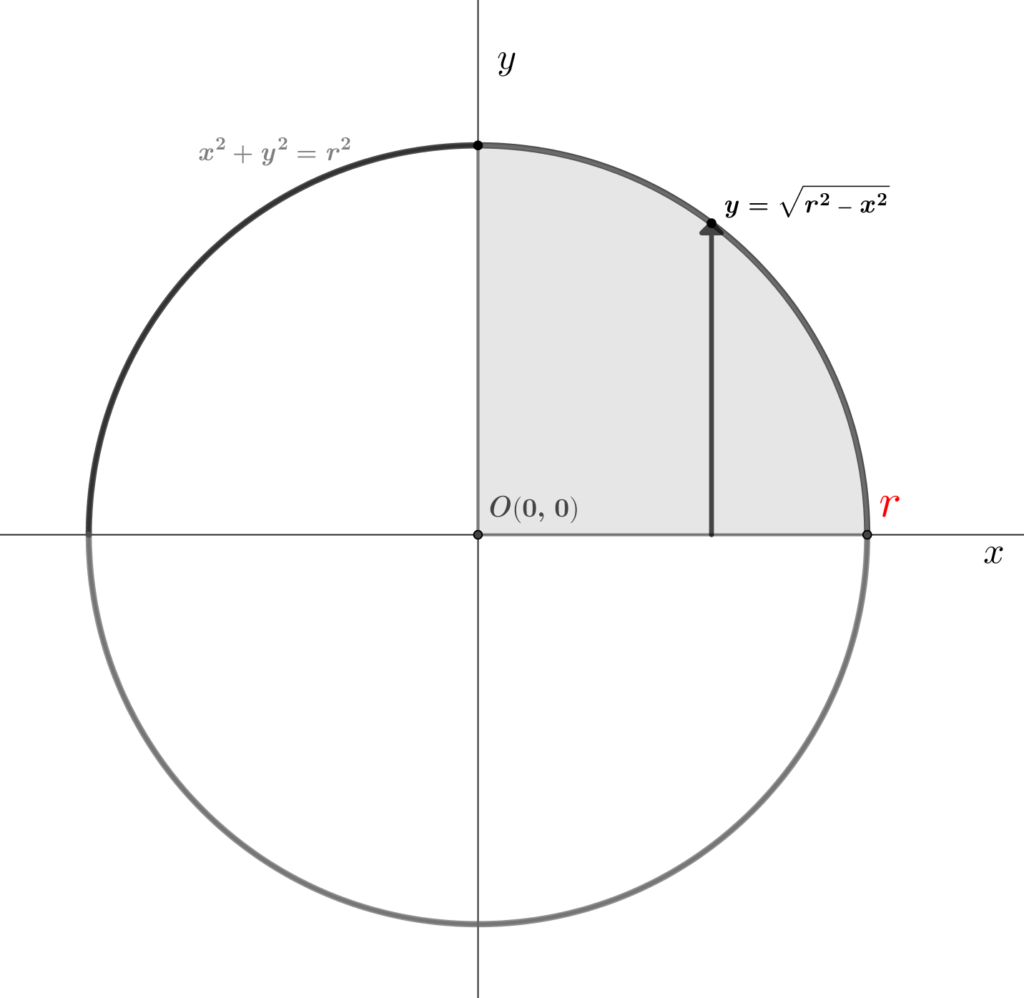
まずは領域を特定してみる。指定の関数 \(x^{2}+y^{2}=r^{2}\) は 中心点の座標が\((0,\,0)\)の \(\href{https://showanojoe.com/template-math/supplementary-material/equation-circle/}{\color{teal}\textsf{円の方程式}}\) である。領域は半径\(r\) の円周以内であることが推測できる。
\(x^{2}{\small\,+\,}y^{2}{\scriptsize\,=\,}r^{2}\)\({\scriptsize \hspace{5pt}\rightarrow\hspace{5pt}}\)\(y^{2}{\scriptsize\,=\,}r^{2}{\small\,-\,}x^{2}{\scriptsize\hspace{5pt}\rightarrow\hspace{5pt}}y{\scriptsize\,=\,}{\small\sqrt{r^{2}{\small\,-\,}x^{2}}}\)
図\(3\) から、\(\small D\small{\scriptsize\,=\,}(x,\,y\,|\, {\scriptsize -}r\:{\tiny \leqq}\hspace{3pt}x \:{\tiny \leqq}\:r,\,{\scriptsize -}{\scriptsize\sqrt{r^{2}-x^{2}}}\:{\tiny \leqq}\hspace{3pt}y \hspace{3pt}{\tiny \leqq}\:{\scriptsize\sqrt{r^{2}-x^{2}}}\,)\)の縦線領域が\(2\)重積分の計算はしやすい。
\(\small\displaystyle\int\!\!\!\int_D x^{2}\,dxdy\hspace{5pt}{\small\,=>\,}\small\displaystyle\int_{-r}^{r}\fcolorbox{gray}{#fff}{$\!\!\int_{-\scriptsize\sqrt{r^{2}-x^{2}}}^{\scriptsize\sqrt{r^{2}-x^{2}}} x^{2}\,dy$}dx\) \({\small\hspace{5pt}=\hspace{5pt}}\small\displaystyle\int_{-r}^{r}{\Large\lbrack}x^{2}y{\Large\rbrack}_{\scriptsize-\sqrt{r^{2}-x^{2}}}^{\scriptsize\sqrt{r^{2}-x^{2}}}\,dx{\small\hspace{5pt}=\hspace{5pt}}2\small\displaystyle\int_{-r}^{r}x^{2}\left({\scriptsize\sqrt{r^{2}-x^{2}}}\right)\,dx\)
区間(上下端)が符号の違い、被積分関数が\(\href{https://showanojoe.com/template-math/graph/#偶関数_奇関数}{\color{teal}\textsf{偶関数}}\)なので、
\({\small\hspace{5pt}=\hspace{5pt}}2\cdot 2\small\displaystyle\int_{0}^{r}x^{2}\left({\scriptsize\sqrt{r^{2}-x^{2}}}\right)\,dx{\small\hspace{5pt}=\hspace{5pt}} 4\small\displaystyle\int_{0}^{r}x^{2}\left({\scriptsize\sqrt{r^{2}-x^{2}}}\right)\,dx\)
右辺の \(4\,\times\,{\scriptsize\displaystyle\int_{0}^{r}x^{2}\left({\scriptsize\sqrt{r^{2}-x^{2}}}\right)\,dx}\)、 すなわち図\(4\)でみる円の面積を\(4\)等分した累次積分の過程となった。
次に \(x\) を \(r\,sin\theta\) と置く。 ☜ 置換積分の\(\href{https://showanojoe.com/template-math/integral/#置換積分_2}{\color{teal}\small\textsf{[事例2]}}\)
\({\scriptsize\displaystyle\frac{dx}{d\theta}}{\small\,=\,}r\,cos\theta{\scriptsize\hspace{5pt}\rightarrow\hspace{5pt}}dx{\small\,=\,}r\,cos\theta\,d\theta\hspace{10pt}x:0\mapsto 1\hspace{5pt}\theta:0\mapsto {\small\displaystyle\frac{\pi}{2}}\) \(\hspace{20pt}\{\small sin\theta{\scriptsize\,=\,}0{\scriptsize\hspace{5pt}\rightarrow\hspace{5pt}}\theta{\scriptsize\,=\,}0,\:sin\theta{\scriptsize\,=\,}1{\scriptsize\hspace{5pt}\rightarrow\hspace{5pt}}\theta{\scriptsize\,=\,}{\scriptsize\displaystyle\frac{\pi}{2}}\hspace{10pt}{\normalsize\textsf{☜}}\,\href{https://showanojoe.com/template-math/trigonometric-function/cosine-trigonometric-ratio/#三角比の盤}{\color{teal}\textsf{三角比}}\}\)
\({\small\hspace{5pt}=\hspace{5pt}}4\small\displaystyle\int_{0}^{\scriptsize\displaystyle\frac{\pi}{2}}sin^{2}\theta{\scriptsize \sqrt{r^{2}\,(1^{2}-sin^{2}\theta})}\,cos\theta\,d\theta\)\({\small\hspace{5pt}=\hspace{5pt}}4\small\displaystyle\int_{0}^{\scriptsize\displaystyle\frac{\pi}{2}}r\,sin^{2}\theta\,{\small cos\theta\,cos\theta\,d\theta}\)\({\small\hspace{5pt}=\hspace{5pt}}4\small\displaystyle\int_{0}^{\scriptsize\displaystyle\frac{\pi}{2}}r\,sin^{2}\theta\,{\small cos^{2}\theta\,d\theta}\)
ここで被積分関数を\(\href{https://showanojoe.com/template-math/trigonometric-function/kastatutory-law/#2倍角の公式}{\color{teal}\textsf{\(2\)倍角の公式}}\)に導く発想をする。
\({\small\hspace{5pt}=\hspace{5pt}}r\small\displaystyle\int_{0}^{\scriptsize\displaystyle\frac{\pi}{2}}4\,sin^{2}\theta\,{\small cos^{2}\theta\,d\theta}\)\({\small\hspace{5pt}=\hspace{5pt}}r\small\displaystyle\int_{0}^{\scriptsize\displaystyle\frac{\pi}{2}}(2sin\theta\,cos\theta)^{2}\,d\theta\)\({\small\hspace{5pt}=\hspace{5pt}}r\small\displaystyle\int_{0}^{\scriptsize\displaystyle\frac{\pi}{2}}sin^{2}2\theta\,d\theta\)
ここで\(\href{https://showanojoe.com/template-math/trigonometric-function/kastatutory-law/#半角の公式}{\color{teal}\textsf{半角公式}}\)に導く発想をする。
\({\small\hspace{5pt}=\hspace{5pt}}r\small\displaystyle\int_{0}^{\scriptsize\displaystyle\frac{\pi}{2}}{\scriptsize\displaystyle\frac{1-cos4\theta}{2}}\,d\theta\)\({\small\hspace{5pt}=\hspace{5pt}}r\cdot {\small\displaystyle\frac{1}{2}}\small\displaystyle\int_{0}^{\scriptsize\displaystyle\frac{\pi}{2}}1-cos4\theta\,d\theta\)\({\small\hspace{5pt}=\hspace{5pt}}{\small\displaystyle\frac{r}{2}}{\Large\lbrack}\theta-{\scriptsize\displaystyle\frac{1}{4}}sin4\theta{\Large\rbrack}_{0}^{\tiny\displaystyle\frac{\pi}{2}}\)
\(1\)を\(\theta\)で積分すると、\(1\cdot \theta\)、 および、\(-cos4\theta\)を\(\theta\)で積分するのに、まずは \(t{\small\,=\,}4\theta{\scriptsize\hspace{5pt}\rightarrow\hspace{5pt}}4d\theta{\small\,=\,}dt\,\)\({\scriptsize\hspace{5pt}\rightarrow\hspace{5pt}}d\theta{\small\,=\,}{\scriptsize\displaystyle\frac{1}{4}}dt\)
なので \({\small\displaystyle\int}{\small cos}{t}\,{\scriptsize\displaystyle\frac{1}{4}}\cdot dt\)\({\scriptsize\hspace{5pt}\rightarrow\hspace{5pt}}{\scriptsize\displaystyle\frac{1}{4}}{\small sin}{t}{\scriptsize\;+\;}C\)\({\scriptsize\hspace{5pt}\rightarrow\hspace{5pt}}{\scriptsize\displaystyle\frac{1}{4}}{\small sin}{4\theta}{\scriptsize\;+\;}C\) よって、\(F\) は \(\theta-{\scriptsize\displaystyle\frac{1}{4}}sin4\theta\) となる。
\({\small\hspace{5pt}=\hspace{5pt}}{\small\displaystyle\frac{r}{2}}\left\{\left({\scriptsize\displaystyle\frac{\pi}{2}}-{\scriptsize\displaystyle\frac{1}{4}}sin2\pi\right)-(0)\right\}\)\({\small\hspace{5pt}=\hspace{5pt}}{\small\displaystyle\frac{r}{2}}\left({\scriptsize\displaystyle\frac{\pi}{2}}-0\right)\)\({\small\hspace{5pt}=\hspace{5pt}}{\small\displaystyle\frac{\pi\,r}{4}}{\color{#00ff7f}\checkmark}\)\(\hspace{25pt}{\small sin2\pi{\scriptsize\;=\;}0}\)\(\hspace{5pt}{\textsf ☜}\,\href{https://showanojoe.com/template-math/trigonometric-function/extension-trigonometric-ratios/#グラフで三角比を表記}{\color{teal}\small\textsf{グラフで三角比を表記}}\)
区分求積法と\(2\)重積分の極座標変換

区分求積法とは、いうなれば 極めて\(0\)に近い微小な概念 に基ずく 極限という「仮想の定義」 である。
区分求積法
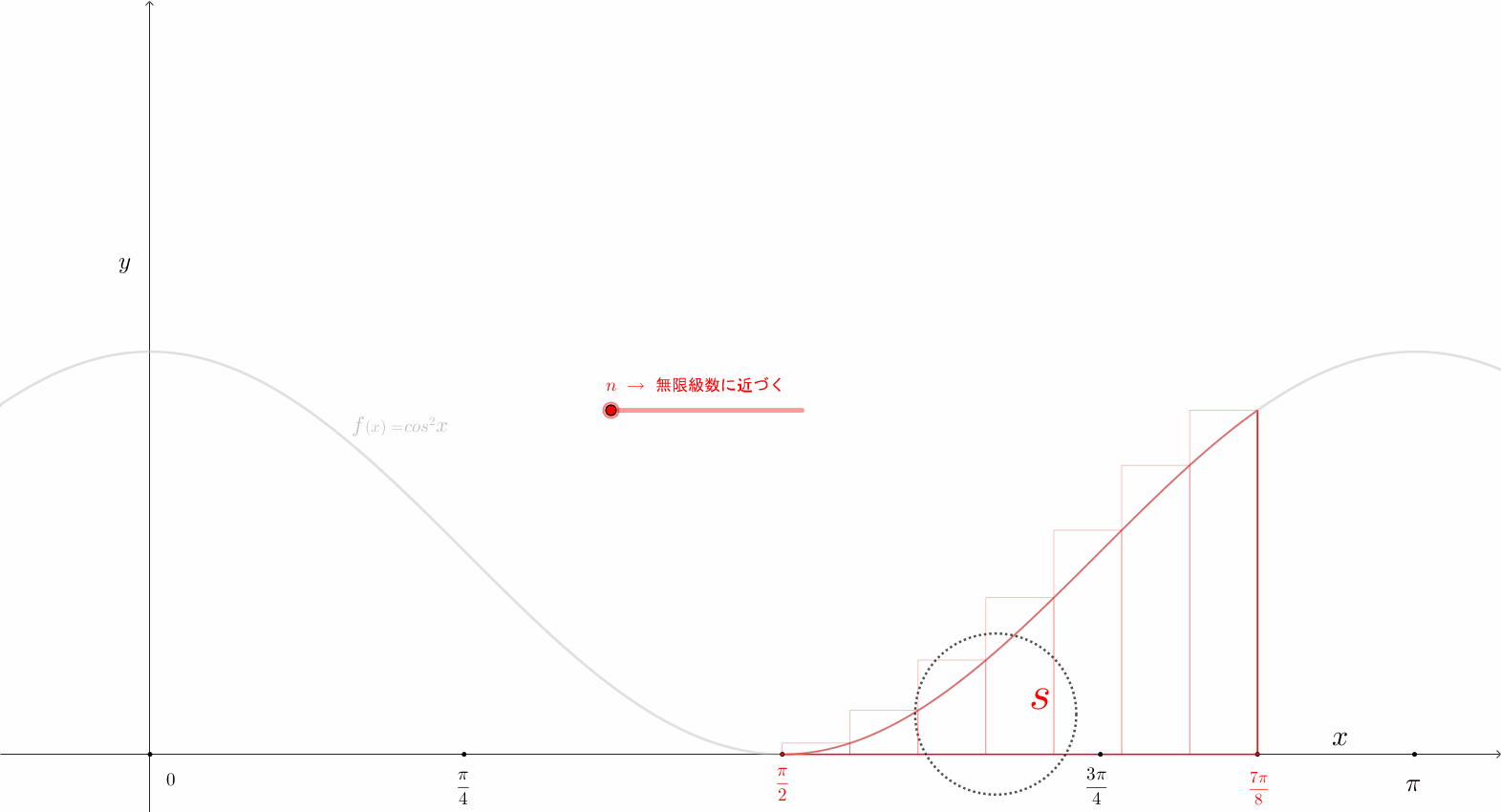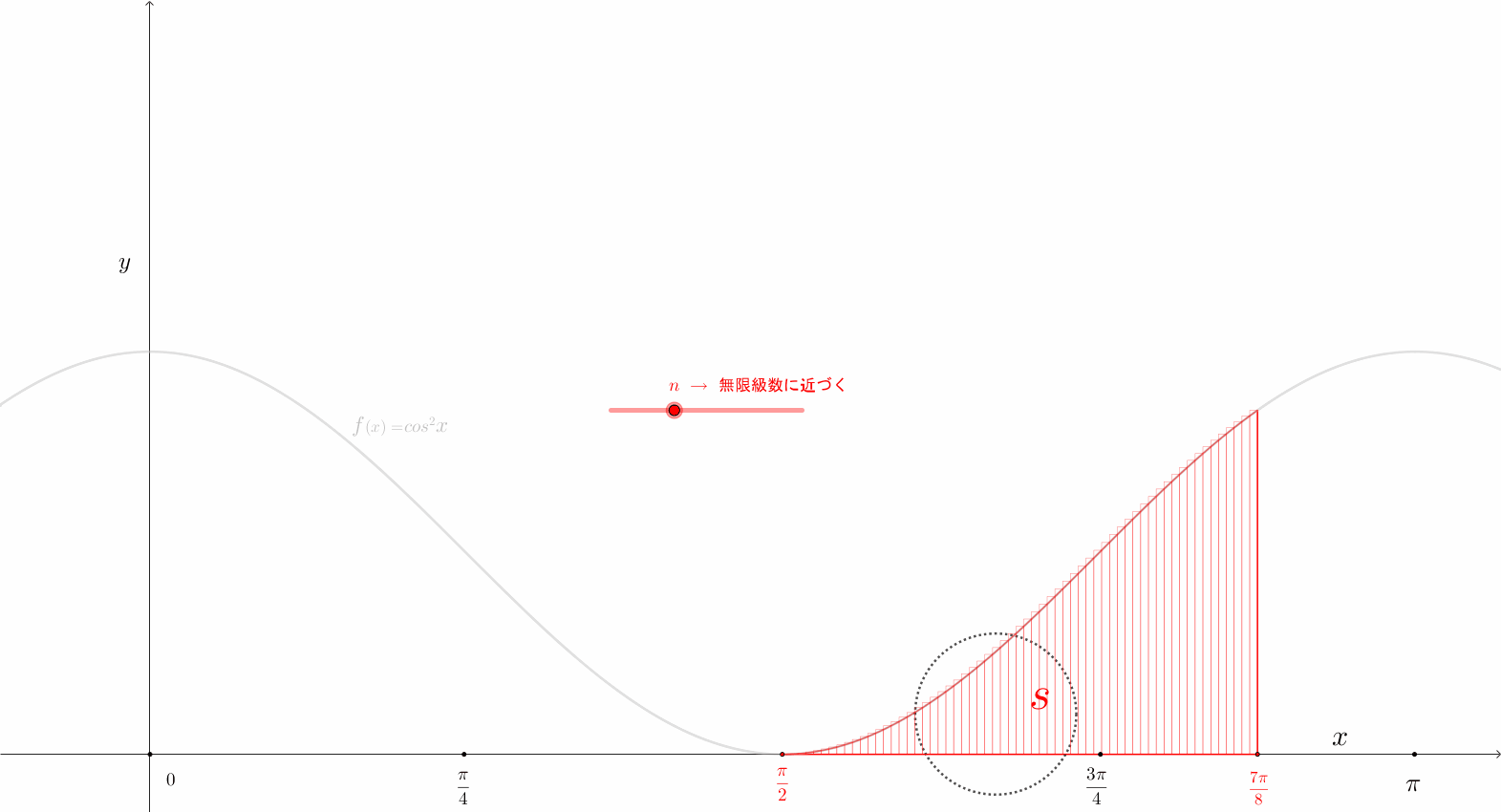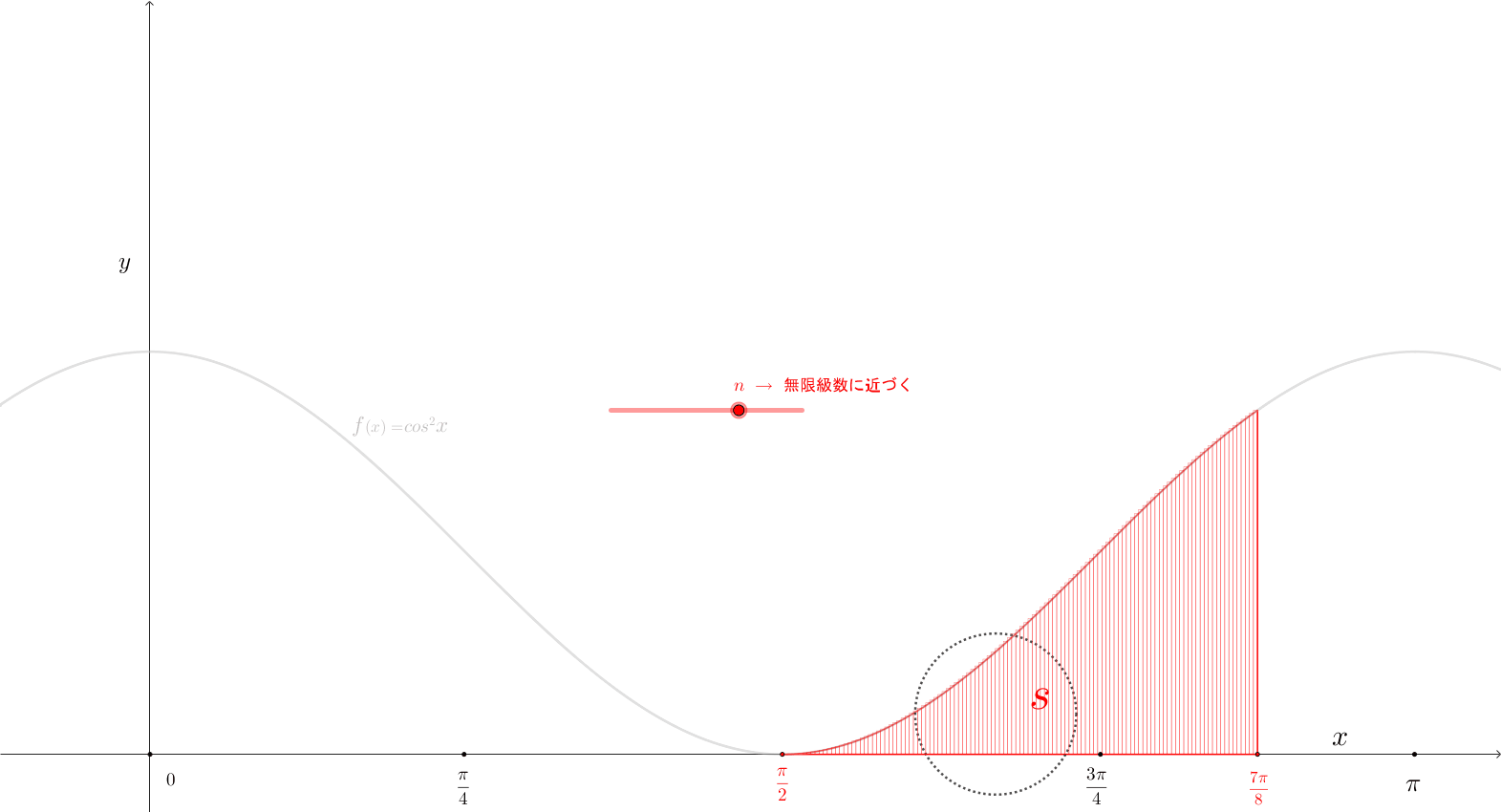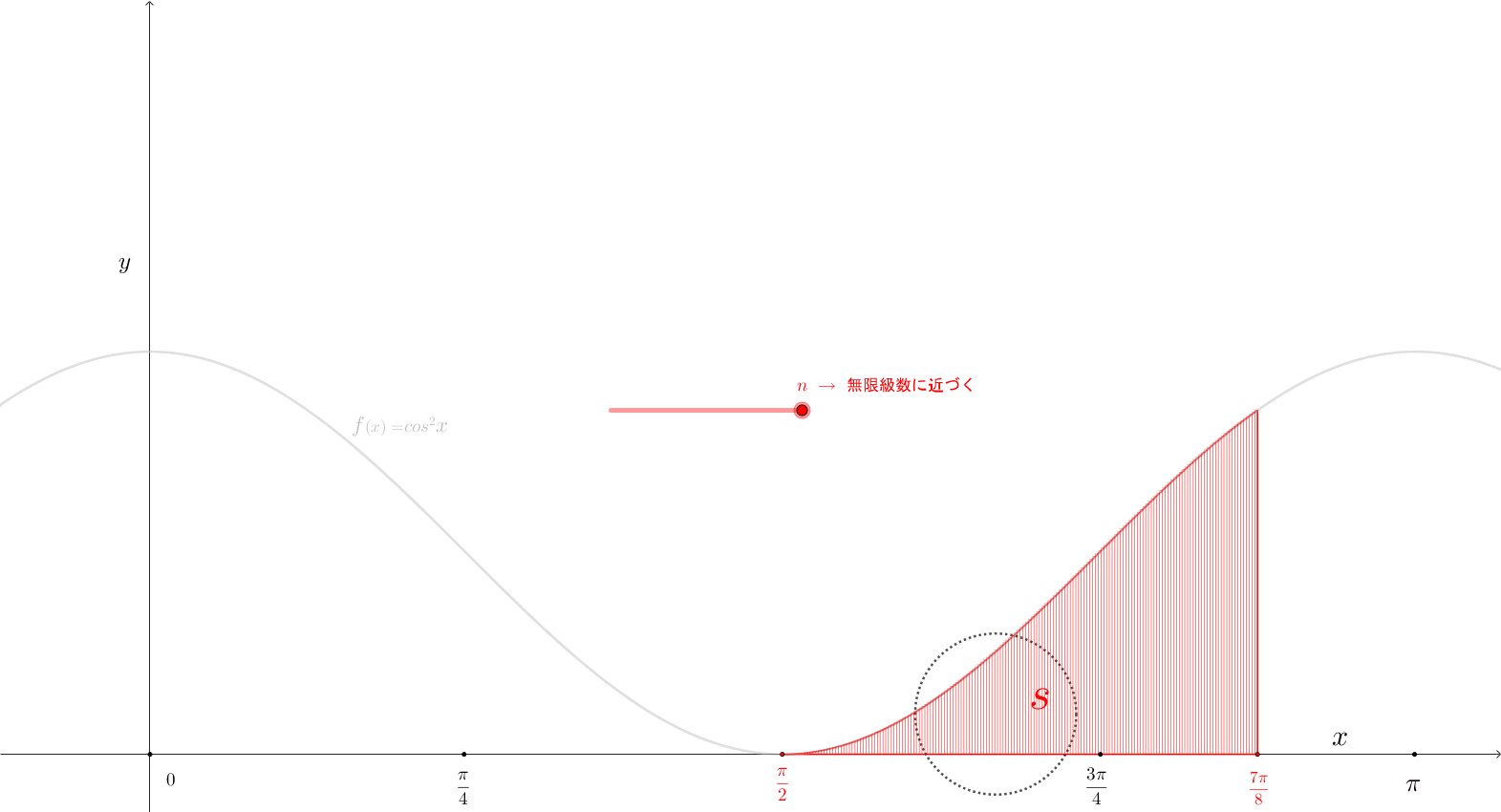
上図\(5\)から、\(y{\small\;=\;}cos^{2}{\large x}\)、 積分区間を \(\scriptsize\displaystyle\frac{\pi}{2}\)\(\small\;\mapsto\;\)\(\scriptsize\displaystyle\frac{7\pi}{8}\) とすると、面積\(S\)は、\(\href{https://showanojoe.com/template-math/integral/#定積分の定義式}{\color{teal}\textsf{定積分の定義式}}\)から求めた。
\(\small\displaystyle\int_{\tiny\displaystyle\frac{\pi}{2}}^{\tiny\displaystyle\frac{7\pi}{8}}\!\!cos^{\scriptsize 2}{x}\,dx\)
\({\small\;=\;}\)\({\huge\lbrack}\left({\small\displaystyle\frac{1}{2}}x{\small\;+\;}{\small\displaystyle\frac{1}{4}sin2x}{\small\;+\;}C\right){\;-\;}\left({\small\displaystyle\frac{1}{2}}x{\small\;+\;}{\small\displaystyle\frac{1}{4}sin2x}{\small\;+\;}C\right){\huge\rbrack}_{\tiny\displaystyle\frac{\pi}{2}}^{\tiny\displaystyle\frac{7\pi}{8}}\)\(\hspace{15pt}\)\(\large\lbrace\;\)☜ 三角関数の積分Ⅲ \(\href{https://showanojoe.com/template-math/trigonometric-function/trigonometric-calculus/#2乗の不定積分公式}{\color{teal}\textsf{2乗の不定積分公式}}\)を参照。\(\large\rbrace\)
\({\small\;=\;}\left({\small\displaystyle\frac{1}{2}}\cdot{\small\displaystyle\frac{7\pi}{8}}{\small\;+\;}{\small\displaystyle\frac{1}{4}sin2\cdot{\small\displaystyle\frac{7\pi}{8}}}\right){\;-\;}\left({\small\displaystyle\frac{1}{2}}\cdot{\small\displaystyle\frac{\pi}{2}}{\small\;+\;}{\small\displaystyle\frac{1}{4}sin2\cdot{\small\displaystyle\frac{\pi}{2}}}\right)\)\(\hspace{15pt}\)\(\large\lbrace\;\) \(\href{https://showanojoe.com/template-math/integral/#積分定数}{\color{teal}\small\textsf{☜}}\;\)積分定数\(C\)は省略。\(\large\rbrace\)
\({\small\;=\;}\left({\small\displaystyle\frac{7\pi}{16}}{\small\;+\;}{\small\displaystyle\frac{1}{4}sin{\displaystyle\frac{7\pi}{4}}}\right){\;-\;}\left({\small\displaystyle\frac{\pi}{4}}{\small\;+\;}{\small\displaystyle\frac{1}{4}sin\pi}\right)\)
\({\small\;=\;}\left({\small\displaystyle\frac{7\pi}{16}}{\small\;+\;}{\small\displaystyle\frac{1}{4}\cdot (-{\displaystyle\frac{\sqrt{2}}{2}}})\right){\;-\;}\left({\small\displaystyle\frac{\pi}{4}}{\small\;+\;}{\small\displaystyle\frac{1}{4}}\cdot{0}\right)\)\(\hspace{15pt}\)\(\large\lbrace\;\)☜ 無料の数式計算サイト \(\href{https://ja.symbolab.com/}{\color{red}\textsf{ja.Symbolab}}\) を使ってみよう。\(\large\rbrace\)
\({\small\;=\;}{\small\displaystyle\frac{7\pi}{16}}{\small\;-\;}{\small\displaystyle\frac{\sqrt{2}}{8}}{\;-\;}{\small\displaystyle\frac{\pi}{4}}\)
\({\small\;=\;}{\small\displaystyle\frac{3\pi}{16}}{\small\;-\;}{\small\displaystyle\frac{\sqrt{2}}{8}}{\small\;=\,}{\small\displaystyle\frac{3\pi-2\sqrt{2}}{16}}{\color{#00ff7f}\checkmark}\)
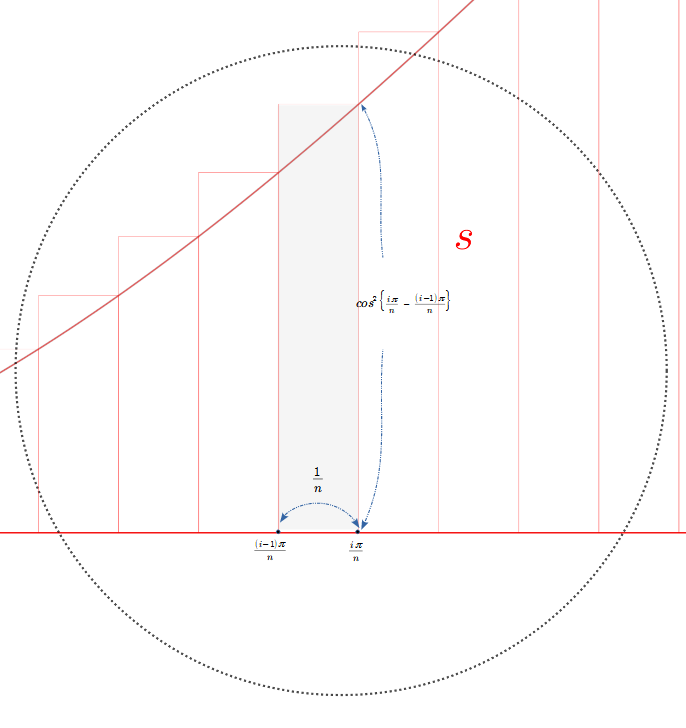
上図\(6\)は図\(5\)のアニメーションを適当な時点で停止して円内を拡大した図である。
面積\(S\) を\(x\)軸に \(n\)分割 した \(i\)\((\)\(1\)から\(n\)までの任意の順番\()\)番目 の長方形の面積は \(\left\{{\scriptsize\displaystyle\frac{i\pi}{n}}{\small\;-\;}{\scriptsize\displaystyle\frac{(i-1)\pi}{n}}\right\}\)\(\cdot cos^{2}\left({\scriptsize\displaystyle\frac{i\pi}{n}}\right)\) になる。
\(i\)番目の長方形の底辺の長さ \(\scriptsize\displaystyle\frac{1}{n}\) は \(\left\{{\scriptsize\displaystyle\frac{i\pi}{n}}{\small\;-\;}{\scriptsize\displaystyle\frac{(i-1)\pi}{n}}\right\}\)、高さは \(f{\small(x)}\)\({\small\;=\;}cos^{\tiny 2}x\) なので、変数\(x\) に \(x\)の座標点 \({\small\displaystyle\frac{i\pi}{n}}\) を代入して \(cos^{\tiny 2}\left\{{\scriptsize\displaystyle\frac{i\pi}{n}}\right\}\) となる。
で、\(1\)番目の長方形 \(\left\{{\scriptsize\displaystyle\frac{1\pi}{n}}{\small\;-\;}{\scriptsize\displaystyle\frac{(1-1)\pi}{n}}\right\}\cdot cos^{2}\left({\scriptsize\displaystyle\frac{1\pi}{n}}\right)\)から\(n\)番目の長方形\(\,\left\{{\scriptsize\displaystyle\frac{n\pi}{n}}{\small\;-\;}{\scriptsize\displaystyle\frac{(n-1)\pi}{n}}\right\}\cdot cos^{2}\left({\scriptsize\displaystyle\frac{n\pi}{n}}\right)\)の面積を足し合わせた面積を面積\(S\)に近づけていく。
これまでを\(\href{https://showanojoe.com/template-math/supplementary-material/sequence/#シグマについて}{\color{\teal}\textsf{総和記号}}\)の式で表すと、
\({\displaystyle\sum_{i=n}^{n}}{\small \left\{{\scriptsize\displaystyle\frac{i\pi}{n}}{\small\;-\;}{\scriptsize\displaystyle\frac{(i-1)\pi}{n}}\right\}\cdot cos^{2}\left({\scriptsize\displaystyle\frac{i\pi}{n}}\right)}\)
\({\small\;=\;}\)\({\huge\lbrack}{\color{red}\underline{\color{black}{\left\{{\scriptsize\displaystyle\frac{1\pi}{n}}{\small\;-\;}{\scriptsize\displaystyle\frac{(1-1)\pi}{n}}\right\}\cdot cos^{2}\left({\scriptsize\displaystyle\frac{1\pi}{n}}\right){\small\;+\;}\left\{{\scriptsize\displaystyle\frac{2\pi}{n}}{\small\;-\;}{\scriptsize\displaystyle\frac{(2-1)\pi}{n}}\right\}\cdot cos^{2}\left({\scriptsize\displaystyle\frac{2\pi}{n}}\right){\small\;+\;}\left\{{\scriptsize\displaystyle\frac{3\pi}{n}}{\small\;-\;}{\scriptsize\displaystyle\frac{(3-1)\pi}{n}}\right\}\cdot cos^{2}\left({\scriptsize\displaystyle\frac{3\pi}{n}}\right){\small\;+\;}}}}\)\(\color{red}\underline{\color{black}{\cdots{\small\;+\;}\left\{{\scriptsize\displaystyle\frac{(i-1)\pi}{n}}{\small\;-\;}{\scriptsize\displaystyle\frac{(i-2)\pi}{n}}\right\}\cdot cos^{2}\left({\scriptsize\displaystyle\frac{(i-1)\pi}{n}}\right){\small\;+\;}\left\{{\scriptsize\displaystyle\frac{i\pi}{n}}{\small\;-\;}{\scriptsize\displaystyle\frac{(i-1)\pi}{n}}\right\}\cdot cos^{2}\left({\scriptsize\displaystyle\frac{i\pi}{n}}\right){\small\;+\;}}}\)\(\hspace{20pt}\color{red}\underline{\color{black}{\cdots{\small\;+\;}\left\{{\scriptsize\displaystyle\frac{(n-1)\pi}{n}}{\small\;-\;}{\scriptsize\displaystyle\frac{(n-2)\pi}{n}}\right\}\cdot cos^{2}\left({\scriptsize\displaystyle\frac{(n-1)\pi}{n}}\right){\small\;+\;}\left\{{\scriptsize\displaystyle\frac{n\pi}{n}}{\small\;-\;}{\scriptsize\displaystyle\frac{(n-1)\pi}{n}}\right\}\cdot cos^{2}\left({\scriptsize\displaystyle\frac{n\pi}{n}}\right)}}\)\({\huge\rbrack}\)
\({\small\;=\;}{\huge\lbrack}{\color{red}\underline{\color{black}{\left\{{\scriptsize\displaystyle\frac{\pi}{n}}\right\}\cdot cos^{2}\left({\scriptsize\displaystyle\frac{1\pi}{n}}\right){\small\;+\;}\left\{{\scriptsize\displaystyle\frac{\pi}{n}}\right\}\cdot cos^{2}\left({\scriptsize\displaystyle\frac{2\pi}{n}}\right){\small\;+\;}\left\{{\scriptsize\displaystyle\frac{\pi}{n}}\right\}\cdot cos^{2}\left({\scriptsize\displaystyle\frac{3\pi}{n}}\right){\small\;+\;}}}}\)\(\color{red}\underline{\color{black}{\cdots{\small\;+\;}\left\{{\scriptsize\displaystyle\frac{\pi}{n}}\right\}\cdot cos^{2}\left({\scriptsize\displaystyle\frac{(i-1)\pi}{n}}\right){\small\;+\;}\left\{{\scriptsize\displaystyle\frac{\pi}{n}}\right\}\cdot cos^{2}\left({\scriptsize\displaystyle\frac{i\pi}{n}}\right){\small\;+\;}}}\)\(\hspace{20pt}\color{red}\underline{\color{black}{\cdots{\small\;+\;}\left\{{\scriptsize\displaystyle\frac{\pi}{n}}\right\}\cdot cos^{2}\left({\scriptsize\displaystyle\frac{(n-1)\pi}{n}}\right){\small\;+\;}\left\{{\scriptsize\displaystyle\frac{\pi}{n}}\right\}\cdot cos^{2}\left({\scriptsize\displaystyle\frac{n\pi}{n}}\right)}}\)\({\huge\rbrack}\)
\({\small\;=\;}{\small\displaystyle\frac{1}{n}}\cdot \pi{\huge\lbrace}{\color{red}\underline{\color{black}{cos^{2}\left({\scriptsize\displaystyle\frac{1\pi}{n}}\right){\small\;+\;}cos^{2}\left({\scriptsize\displaystyle\frac{2\pi}{n}}\right){\small\;+\;} cos^{2}\left({\scriptsize\displaystyle\frac{3\pi}{n}}\right){\small\;+\;}}}}\)\(\color{red}\underline{\color{black}{\cdots{\small\;+\;}cos^{2}\left({\scriptsize\displaystyle\frac{(i-1)\pi}{n}}\right){\small\;+\;}cos^{2}\left({\scriptsize\displaystyle\frac{i\pi}{n}}\right){\small\;+\;}}}\)\(\hspace{20pt}\color{red}\underline{\color{black}{\cdots{\small\;+\;} cos^{2}\left({\scriptsize\displaystyle\frac{(n-1)\pi}{n}}\right){\small\;+\;}cos^{2}\left({\scriptsize\displaystyle\frac{n\pi}{n}}\right)}}\)\({\huge\rbrace}\)
それで、積分区間が \(x:{\scriptsize\displaystyle\frac{\pi}{2}}\hspace{5pt}{\small\mapsto}\hspace{5pt}{\scriptsize\displaystyle\frac{7\pi}{8}}\) なので\((\)図\(5\)\()\)、
\({\small\;=\;}{\small\displaystyle\frac{1}{n}}\cdot \pi{\displaystyle\sum_{i={\tiny\displaystyle\frac{1}{2}}n}^{{\tiny\displaystyle\frac{7}{8}}n}}\small cos^{2}\left({\scriptsize\displaystyle\frac{i\pi}{n}}\right)\)
となる。
それで、上記の\(\href{https://showanojoe.com/template-math/supplementary-material/sequence/#数列の定義}{\color{teal}\textsf{数列}}\)を級数\((\)\(n\)を無限分割する\()\)とし、\(\large S\) を\(n\)分割した\(1\)番目の長方形を 初項、\(i\)番目の長方形は 第\(i\)項 に見立てることができる。
長方形の 級数\((\small\textsf{分割する長方形の数})\)を無限とし、収束\((\small\textsf{ある極限値に限りなく近い値に近づける})\)させて面積\(\large S\)を導出する手法が\(\href{https://showanojoe.com/template-math/integral/#定積分}{\color{teal}\textsf{定積分の定義式}}\)の構造である区分求積法である。
\(n\)分割を無限分割にする \((\small\textsf{$n$を$\infty$に拡散する})\)という上述の\(\href{https://showanojoe.com/template-math/limits-and-derivatives/#極限}{\color{teal}\textsf{極限}}\)から \({\it{lim}}_{\overset{\Large{~^~}}{\hspace{-25pt}{\scriptsize{n\scriptsize{\rightarrow}\scriptsize \infty}}}}\!\!{\displaystyle\frac{1}{n}}{\displaystyle\sum_{i=1}^{n}}\small cos^{2}\left({\scriptsize\displaystyle\frac{i\pi}{n}}\right)\) という式が得られる。以下にこの極限を導出する。
\({\small\it{lim}}_{\overset{\Large{~^~}}{\hspace{-25pt}{\scriptsize{n\scriptsize{\rightarrow}\scriptsize \infty}}}}\!\!{\displaystyle\frac{1}{n}}{\displaystyle\sum_{i=1}^{n}}\small cos^{2}\left({\scriptsize\displaystyle\frac{7}{8}}\cdot{\scriptsize\displaystyle\frac{i}{n}}\right)\)
\({\small\;=\;}{\small\it{lim}}_{\overset{\Large{~^~}}{\hspace{-25pt}{\scriptsize{n\scriptsize{\rightarrow}\scriptsize \infty}}}}\!\!{\displaystyle\frac{1}{n}}{\displaystyle\sum_{i=1}^{n}}\small cos^{2}\left({\scriptsize\displaystyle\frac{7}{8}}\cdot{\scriptsize\displaystyle\frac{i\pi}{n}}\right)\)
\({\small\;=\;}{\small\it{lim}}_{\overset{\Large{~^~}}{\hspace{-25pt}{\scriptsize{n\scriptsize{\rightarrow}\scriptsize \infty}}}}{\displaystyle\frac{1}{n}}{\scriptsize\displaystyle\frac{n(n+1)(2n+1)}{6}}{\small\;+\;}{\small\it{lim}}_{\overset{\Large{~^~}}{\hspace{-25pt}{\scriptsize{n\scriptsize{\rightarrow}\scriptsize \infty}}}}\!\!{\displaystyle\frac{1}{n}}n\cdot 1\)\({\small\;=\;}{\small\it{lim}}_{\overset{\Large{~^~}}{\hspace{-25pt}{\scriptsize{n\scriptsize{\rightarrow}\scriptsize \infty}}}}{\scriptsize\displaystyle\frac{(n+1)(2n+1)}{6}}{\small\;+\;}{\small\it{lim}}_{\overset{\Large{~^~}}{\hspace{-25pt}{\scriptsize{n\scriptsize{\rightarrow}\scriptsize \infty}}}}\!1\)
\({\small\;=\;}{\small\it{lim}}_{\overset{\Large{~^~}}{\hspace{-25pt}{\scriptsize{n\scriptsize{\rightarrow}\scriptsize \infty}}}}\scriptsize\displaystyle\frac{\left\{cos\left({\scriptsize\displaystyle\frac{i}{n}}\right)^{2}+1\right\}\left\{2cos\left({\scriptsize\displaystyle\frac{i}{n}}\right)^{2}+1\right\}}{6}{\small\;+\;}{\small\it{lim}}_{\overset{\Large{~^~}}{\hspace{-25pt}{\scriptsize{n\scriptsize{\rightarrow}\scriptsize \infty}}}}\!1\)
極座標変換による\(2\)重積分の解法
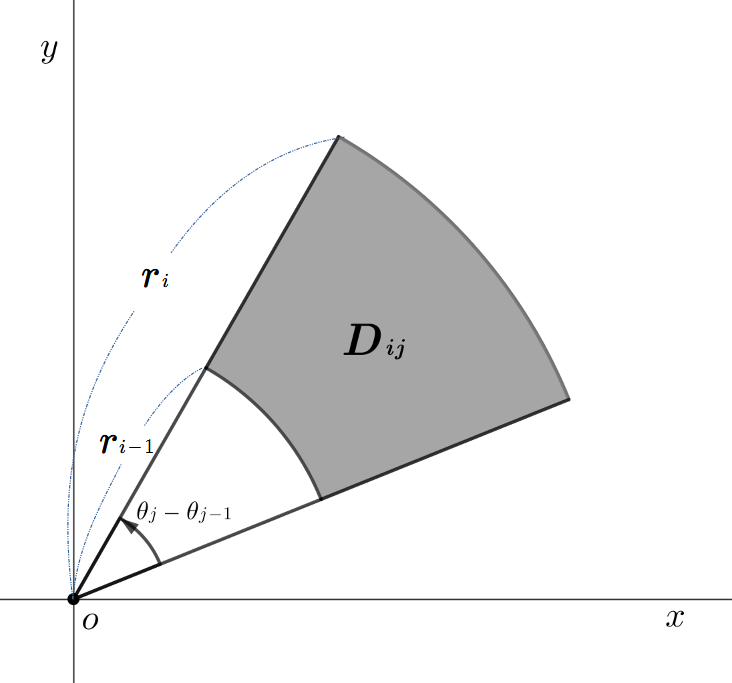
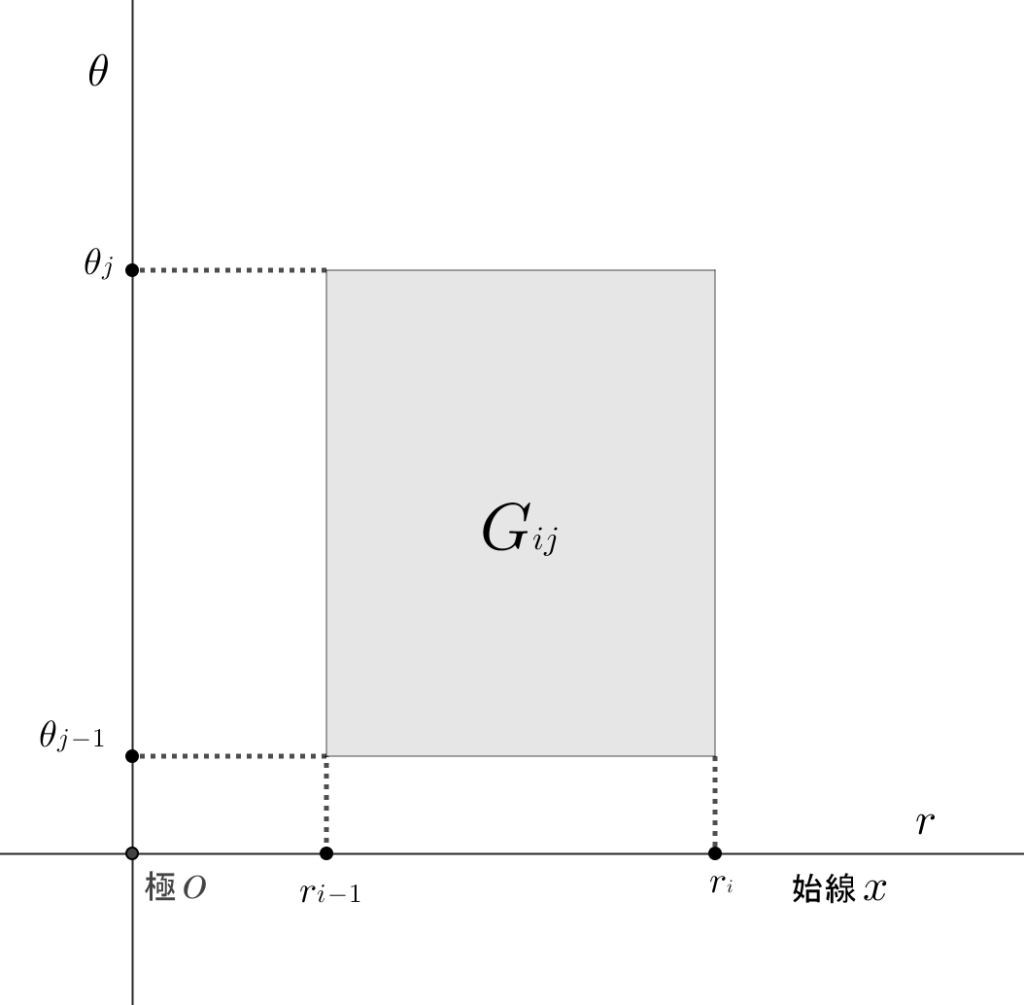
\(2\)重積分の直交座標から極座標への変換公式 \(\small\displaystyle\int\!\!\!\int_D {\large f}{\small (x,\,y)}\,dxdy\)\({\small\hspace{10pt}\Rightarrow\hspace{10pt}}\small\displaystyle\int\!\!\!\int_G {\large f}{\small (rcos\theta,\,rsin\theta)}\,{\color{red}r}\,drd\theta\)
\(\color{red}r\) についての解説を以下に記述する。\(\{\)まずは 雛形数学二部の \(\href{https://showanojoe.com/template-math/supplementary-material/polar-coordinates_polar-equations/#極座標}{\color{teal}\textsf{極座標}}\) を参照のこと。\(\}\)
扇形の面積は \(\pi r^{2}\times \small\displaystyle\frac{\theta}{2\pi}\) で導出できる。よって、図\(5\)の半径 \(r{\tiny i}\) の扇形の面積は \(\pi r^{\small2}\!\!{\tiny i}\times \small\displaystyle\frac{\theta{\tiny j}{\small\,-\,}\theta{\tiny j-1}}{2\pi}\)、半径 \(r{\tiny i-1}\) の扇形の面積は \(\pi r^{\small 2}\!\!{\tiny i-1}\times \small\displaystyle\frac{\theta{\tiny j}{\small\,-\,}\theta{\tiny j-1}}{2\pi}\) なので、面積 \(D{\scriptsize i\,j}\) は \(\pi r^{\small2}\!\!{\tiny i}\times \small\displaystyle\frac{\theta{\tiny j}{\small\,-\,}\theta{\tiny j-1}}{2\pi}\)\({\small \;-\;}\pi r^{\small 2}\!\!{\tiny i-1}\times \small\displaystyle\frac{\theta{\tiny j}{\small\,-\,}\theta{\tiny j-1}}{2\pi}\) となる。
\({\cancel{\pi}} r^{\small2}\!\!{\tiny i}\times \small\displaystyle\frac{\theta{\tiny j}{\small\,-\,}\theta{\tiny j-1}}{2\cancel{\pi}}\)\({\small \;-\;}{\cancel{\pi}} r^{\small 2}\!\!{\tiny i-1}\times \small\displaystyle\frac{\theta{\tiny j}{\small\,-\,}\theta{\tiny j-1}}{2\cancel{\pi}}\)\({\small\;=\;}{\small\displaystyle\frac{1}{2}}(r^{\small2}\!\!{\tiny i}{\small\,-\,}r^{\small 2}\!\!{\tiny i-1})(\theta{\tiny j}{\small\,-\,}\theta{\tiny j-1})\)\({\small\;=\;}{\small\displaystyle\frac{1}{2}}(r{\tiny i}{\small\,-\,}r{\tiny i-1})(r{\tiny i}{\small\,+\,}r{\tiny i-1})(\theta{\tiny j}{\small\,-\,}\theta{\tiny j-1})\)
それで \(r{\tiny i}\) と \(r{\tiny i\!-\!1}\) は限りなく微小であるという極限の
\(r{\tiny i}{\scriptsize\,+\,}r{\tiny i-1}{\scriptsize\,=\,}2r{\tiny i}(\small\textsf{または}\,{\small2}r{\tiny i-1})\) から \({\small\displaystyle\frac{1}{2}}(r{\tiny i}{\small\,-\,}r{\tiny i-1})(r{\tiny i}{\small\,+\,}r{\tiny i-1})(\theta{\tiny j}{\small\,-\,}\theta{\tiny j-1})\)\({\small\;=\;}r{\tiny i}(r{\tiny i}{\small\,+\,}r{\tiny i-1})(\theta{\tiny j}{\small\,-\,}\theta{\tiny j-1})\)、
\((r{\tiny i}{\small\,+\,}r{\tiny i-1})(\theta{\tiny j}{\small\,-\,}\theta{\tiny j-1})\) は図\(6\)の 面積\(|G{\scriptsize i\!j}|\) なので、\(r{\tiny i}(r{\tiny i}{\small\,+\,}r{\tiny i-1})(\theta{\tiny j}{\small\,-\,}\theta{\tiny j-1})\)\({\scriptsize\,=\,}r{\tiny 1}|G{\scriptsize i\!j}|\) となる。
以上から、区分求積法で表すと \({\it{lim}}_{\overset{\Large{~^~}}{\hspace{-25pt}{\scriptsize{x\scriptsize{\rightarrow}\scriptsize \infty}}}}\)\(\!\!\displaystyle \sum_{i,\,j=1}^n {\large f}{\small(r{\tiny i}cos\theta{\tiny j},\,r{\tiny i}sin\theta{\tiny j})}\)\(\cdot r{\tiny i}|G{i\!j}|\) となり、極座標における\(2\)重積分の式は \(\small\displaystyle\int\!\!\!\int_G {\color{red}\large r}{\large f}{\small (rcos\theta,\,rsin\theta)}\,drd\theta\) となる。
\(\color{gray}\textsf{[事例$1$]}\)
\(\small\displaystyle\int\!\!\!\int_D x\,dxdy\)\(\hspace{20pt}\)\(D:x^{2}{\small\;+\;}y^{2}{\scriptsize\;\leqq\;}2x\)\(\hspace{5pt}\)
\(\hspace{150pt}\)の\(2\)重積分を求めてみる。
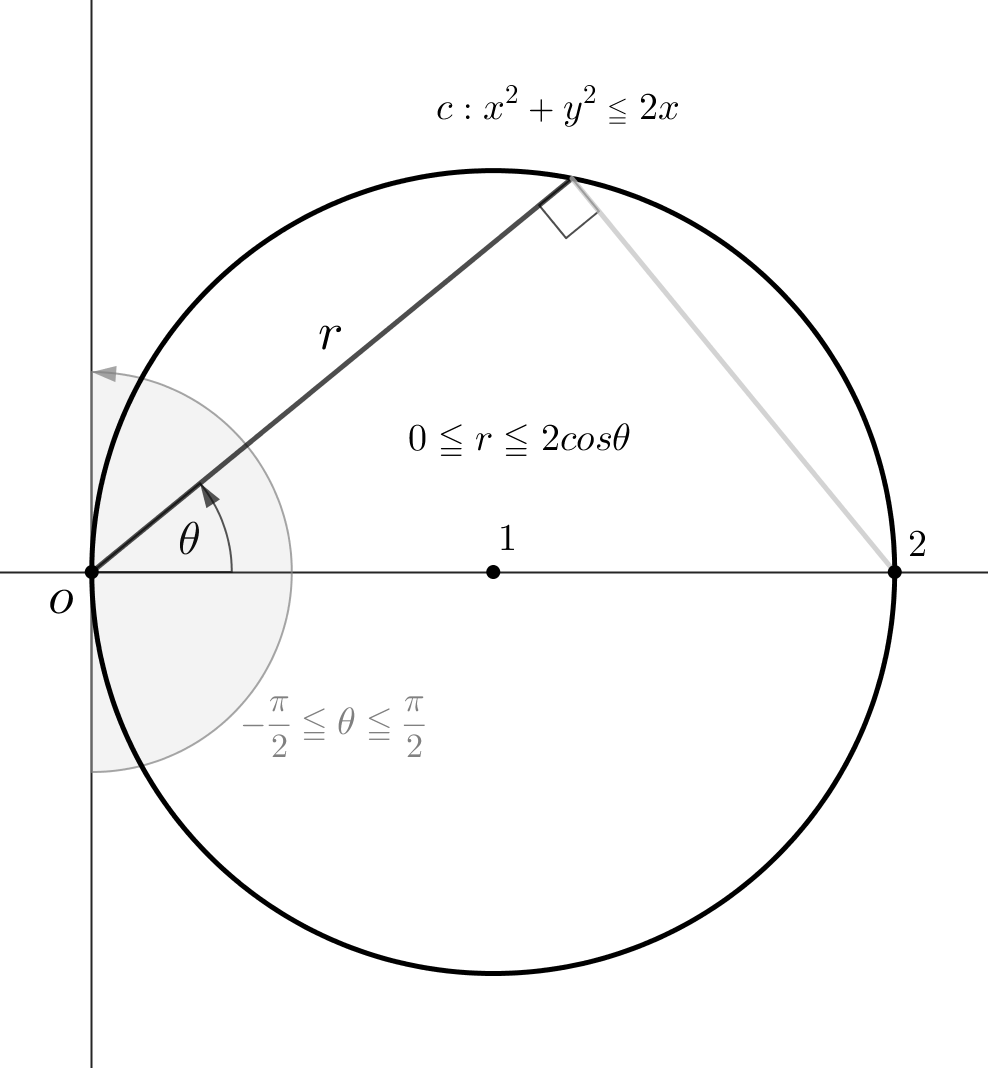
まずは円の方程式が \(x^{2}{\small\;+\;}y^{2}{\scriptsize\;\leqq\;}2x\) ということなので、この\(\href{https://showanojoe.com/template-math/supplementary-material/inequality/}{\color{teal}\textsf{$2$次不等式}}\)を式変形して図示しやすい\(\href{https://showanojoe.com/template-math/supplementary-material/equation-circle/}{\color{teal}\textsf{円の方程式}}\)にする。
\(x^{2}{\small\;+\;}y^{2}{\scriptsize\;\leqq\;}2x\)\(\hspace{10pt}\small\Rightarrow\hspace{10pt}\)\(x^{2}{\small\;+\;}y^{2}{\small\;-\;}2x{\scriptsize\;\leqq\;}0\) この式を\(\href{https://showanojoe.com/template-math/graph/#平方完成}{\color{teal}\textsf{平方完成}}\)により \(\hspace{5pt}\small\Rightarrow\hspace{10pt}\)\((x^{2}{\small -}2x{\small +}1){\small\;-\;}1{\small \;+\;}y^{2}{\scriptsize\;\leqq\;}0\)\(\hspace{10pt}\small\Rightarrow\hspace{10pt}\)\((x{\small -}1)^{2}{\small\;-\;}1{\small \;+\;}y^{2}{\scriptsize\;\leqq\;}0\)\(\hspace{10pt}\small\Rightarrow\hspace{10pt}\)\((x{\small -}1)^{2}{\small \;+\;}y^{2}{\scriptsize\;\leqq\;}1\)
これで求まる\(2\)重積分の領域は中心が \(x{\small\;=\;}1\)、\(x{\small\;=\;}0\) の座標点の半径 \(1\) の円である察しが付く。
この円の領域の 偏角\(\theta\) の範囲は \(\color{gray}{\small -}\small\displaystyle\frac{\pi}{2}{\small\;\leqq\;}{\theta}{\small\;\leqq\;}\small\displaystyle\frac{\pi}{2}\)。
距離\(r\) の範囲は、\(\href{https://showanojoe.com/template-math/trigonometric-function/cosine-trigonometric-ratio/#直角三角形の三角比}{\color{teal}\textsf{直角三角形の三角比}}\)に着目して \(r{\small\;=\;}{\large f}{\small(\theta)}\) の方程式 \(\small\displaystyle\frac{r}{2}{\small\;=\;}cos\theta\)\(\hspace{10pt}\small\Rightarrow\hspace{10pt}\)\(r{\small\;=\;}2cos\theta\) の偏角\(\theta\) が変化すると 距離\(r\) も変化する関数の方程式になる。上図から 距離\(r\)の最大値は \(2\) であることは明白である。それでその時の偏角は \(\href{https://showanojoe.com/template-math/trigonometric-function/cosine-trigonometric-ratio/#三角比の表}{\color{teal}\textsf{$cos0{\small\;=\,}1$}}\) なので距離\(r\) の範囲は \(0{\scriptsize\;\leqq\;}r{\scriptsize\;\leqq\;}2cos\theta\) となる。以下に続けよう。
\(\small\displaystyle\int\!\!\!\int_D x\,dxdy\)\(\hspace{10pt}\)\(D:x^{2}{\small\;+\;}y^{2}\)\(\hspace{10pt}\small\Rightarrow\hspace{10pt}\)\(\small\displaystyle\int\!\!\!\int_G {\color{red}r}\,r\,cos\theta\,drd\theta\)\(\hspace{10pt}\)\(G:0{\scriptsize\;\leqq\;}r{\scriptsize\;\leqq\;}2cos\theta\)\(,\,{\small -}\small\displaystyle\frac{\pi}{2}{\small\;\leqq\;}{\theta}{\small\;\leqq\;}\small\displaystyle\frac{\pi}{2}\)
\(\hspace{10pt}\small\Rightarrow\hspace{10pt}\)\(\small\displaystyle\int_{\tiny-\displaystyle\frac{\pi}{2}}^{\tiny\displaystyle\frac{\pi}{2}}\!\fcolorbox{#C0C0C0}{#fff}{$\!\int_{\scriptsize 0}^{\scriptsize 2cos\theta}r^{2}\,cos\theta\,dr$}d\theta\)\(\small\hspace{5pt}=\hspace{5pt}\)\(\small\displaystyle\int_{\tiny-\displaystyle\frac{\pi}{2}}^{\tiny\displaystyle\frac{\pi}{2}}{\LARGE\lbrack}{\small\displaystyle\frac{r^{3}}{3}}cos\theta{\LARGE\rbrack}_{0}^{2cos\theta}d\theta\)\(\small\hspace{5pt}=\hspace{5pt}\)\(\small\displaystyle\int_{\tiny-\displaystyle\frac{\pi}{2}}^{\tiny\displaystyle\frac{\pi}{2}}{\small\displaystyle\frac{(2cos\theta)^{3}}{3}}cos\theta{\small\;-\;}0\,d\theta\)
\(\small\hspace{5pt}=\hspace{5pt}\)\({\small\displaystyle\frac{8}{3}}\small\displaystyle\int_{\tiny-\displaystyle\frac{\pi}{2}}^{\tiny\displaystyle\frac{\pi}{2}}cos^{4}\theta\,d\theta\)
\(\href{https://showanojoe.com/template-math/graph/#偶関数_奇関数}{\color{teal}\textsf{偶関数}}\)の性質により係数が\(2\)倍されて、
\(\small\hspace{5pt}=\hspace{5pt}\)\({\small\displaystyle\frac{16}{3}}\small\displaystyle\int_{\tiny-\displaystyle\frac{\pi}{2}}^{\tiny\displaystyle\frac{\pi}{2}}cos^{4}\theta\,d\theta\)
被積分関数\(cos^{4}x\) を\(\href{https://showanojoe.com/template-math/integral/#定積分の漸化式を2重階乗で表記}{\color{teal}\textsf{漸化式の\(2\)重階乗}}\)で表すと、
\(\small\hspace{5pt}=\hspace{5pt}\)\({\small\displaystyle\frac{16}{3}}\)\(\cdot{\Large\lbrack}\;\)\(\color{red}\underline{\color{black}{\small\displaystyle\frac{\pi}{2}}\cdot{\small\displaystyle\frac{(4-1)!!}{4!!}}}\)\(\;{\Large\rbrack}\)
\(\small\hspace{5pt}=\hspace{5pt}\)\({\small\displaystyle\frac{16}{3}}\cdot{\small\displaystyle\frac{3\pi}{16}}\)\(\small\hspace{5pt}=\hspace{5pt}{\large\pi}{\color{#00ff7f}\checkmark}\)
