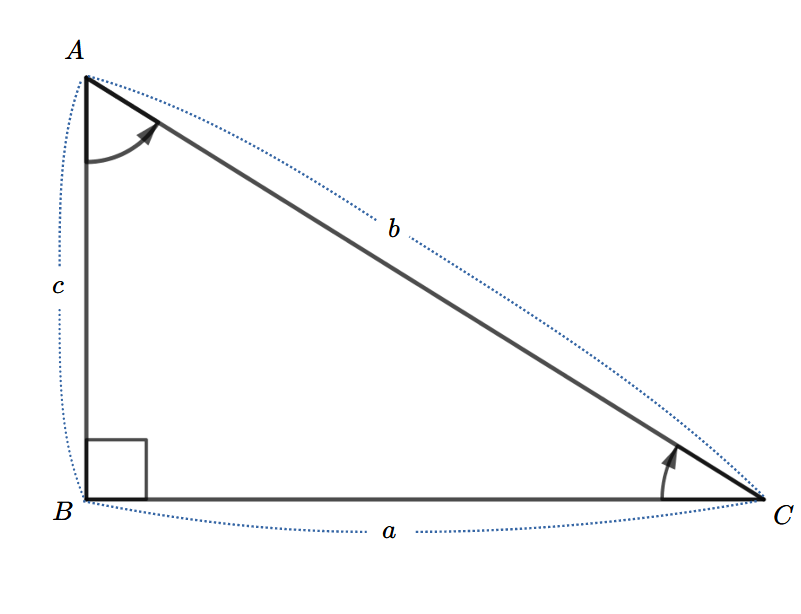
余弦定理とは、任意の二辺の長さとそれに挟まれる内角の大きさが提示されれば、対辺\((\)その提示された内角に向かい合う課題の辺\()\)の長さが特定出来る三角形の定理をいう。
\({\textsf{余弦定理の公式}}\left\{\begin{array}{l}{a^2}{\small\;=\;}{b^2+c^2}-2bc\,cosA\\ {b^2}{\small\;=\;}{a^2+c^2}-2ac\,cosB\\ {c^2}{\small\;=\;}{a^2+b^2}-2ab\,cosC\end{array}\right.\)
上図1より以下、
鋭角\(\angle{\alpha}\)\(({\scriptsize 0^{\,\circ}<\angle{\small\alpha}<\,90^{\,\circ}})\)の\({\it\Delta} ABC \)の余弦定理の証明
\(\overline{BC}={\large\it a},\;\overline{AC}={\large\it b},\;\overline{AB}={\large\it c}\)とする。
\(C\) から \(c\) に垂線を引き、その交点を\({\color{red}{H_1}}\) とする。
\({\it\Delta} BC{\color{red}H_1}\overline{AC}={b},~~\overline{C\color{red}H_1}=bsin{\large\alpha}\left(\Leftarrow\;sin{\large\alpha}=\displaystyle{\frac{\overline{C{\color{red}H_1}}}{b}}\right)\)
\(\overline{B{\color{red}H_1}}={c}-{b}\,cos{\large\alpha}\left( \Leftarrow\;{b}\,cos\alpha=c-\overline{B\color{red}{H_1}}\left(=\overline{A\color{red}{H_1}}\right)\Leftarrow\;cosA=\displaystyle{\frac{\overline{c-B{\color{red}{H_1}}}}{b}}\right)\)
\(\href{https://showanojoe.com/template-math/trigonometric-function/three-squares-theorem/}{\color{teal}\textsf{三平方の定理}}\)により、\({a^2}={(b\,sin{\large\alpha})^2}+{(c-b\,cos\alpha)^2}\)
\({a^2}={b^2\,cos^2 {\large\alpha}}+{c^2-2bc\,cos\alpha+b^2 cos^2 {\large\alpha}}\)
\({a^2}={b^2\,(cos^2 \alpha+sin^2 {\large\alpha})+c^2-2bc\,cos{\large\alpha}}\)\(\hspace{10pt}\) ☜ \(\href{https://showanojoe.com/template-math/trigonometric-function/extension-trigonometric-ratios/#三角比の相互関係式}{\color{teal}\textsf{三角比の相互関係式}}\) \(cos^2 \theta+sin^2 \theta=1\)
\({a^2}={b^2\cdot 1+c^2-2bc\,cos{\large\alpha}}\)
\({a^2}={b^2+c^2-2bc\,cos{\large\alpha}} ~~~~\left\{b,c\,\textsf{も同様の過程で証明できる。}\right\}\)
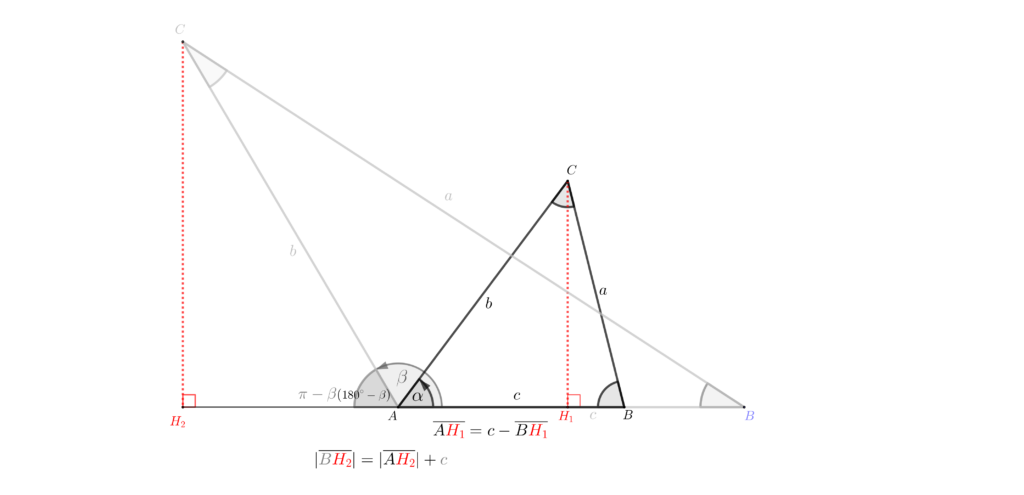
鈍角\(\angle{\large\beta}\)\(({\scriptsize 90^{\,\circ}<\angle{\small\beta}<\,180^{\,\circ}})\)の\({\it\Delta} A{\color{gray}{BC}}\)の余弦定理の証明
\(\overline{{\color{gray}{BC}}}={\large\it{\color{gray}{a}}},\;\overline{A{\color{gray}{C}}}={\large\it{\color{gray}{b}}},\;\overline{A{\color{gray}{B}}}={\large\it{\color{gray}{c}}}\)とする。
\({\color{gray}{C}}\) から \({\color{gray}{c}}\) の延長線上に垂線を引き、その交点を\({\color{red}{H_2}}\) とする。
\(\angle{\color{gray}C}A{\color{red}{H_2}}=\angle({\color{darkgray}{\pi-\beta}})\) とおく。
\({\it\Delta}{\color{darkgray}{BC}}{\color{red}{H_2}} \overline{A{\color{darkgray}C}}={\color{darkgray}b},~~\overline{\color{darkgray}C{\color{red}{H_2}}}={\color{darkgray}b}\,sin{\color{gray}{\large\beta}}\hspace{15pt} \left\{\Leftarrow\;sin\,({\color{gray}{\pi-\beta}})=\displaystyle{\frac{\overline{{\color{darkgray}C}{\color{red}{H_2}}}}{\color{darkgray}b}}\right\}\)
\(\small{cos\,(\pi-\beta)=cos(-\beta),\;sin\,(\pi-\beta)=sin\,\beta}\)\(\hspace{10pt}\)☜ \(\href{https://showanojoe.com/template-math/trigonometric-function/extension-trigonometric-ratios/#\(\textsf{$\measuredangle{\alpha}$ の三角比の拡張}\)}{\color{teal}\textsf{$\measuredangle{\alpha}$の三角比の拡張}}\) を参照。
\(\overline{{\color{darkgray}B}{\color{red}H_2}}={\color{darkgray}c}+(-{\color{darkgray}b}\,cos\,{\color{gray}\large\beta})\Leftarrow\, \overline{{\color{darkgray}B}{\color{red}H_2}}={\color{darkgray}c}+\; \overline{A{\color{red}H_2}} (\small{{\color{darkgray}b}\,cos(-{\color{gray}\beta})})\)
三平方の定理により、\({\color{darkgray}a}^2=({\color{darkgray}b}\,sin{\color{gray}{\large\beta}})^2+({\color{darkgray}c}-{\color{darkgray}b}\,cos{\color{gray}\large\beta})^2\)
\({{\color{darkglay}a}^2}={{\color{darkgray}b}^2\,cos^2\,{\color{gray}\large\beta}}+{{\color{darkgray}c}^2-2{\color{darkgray}bc}\,cos\,{\color{gray}\large\beta}+{\color{darkgray}b}^2 cos^2\,{\color{gray}\large\beta}}\)
\({{\color{darkgray}a}^2}={{\color{darkgray}b}^2\,(cos^2 \,{\color{gray}\large\beta}+sin^2\, {\color{gray}\large\beta})+ {\color{darkgray} c}^2-2{\color{darkgray}bc}\,cos\,{\color{gray}\large\beta}}\)\(\hspace{15pt}\)☜ 三角形の相互関係式 \(cos^2 \theta+sin^2 \theta=1\)
\({{\color{darkgray}a}^2}={{\color{darkgray}b}^2\cdot 1+{\color{darkgray}c}^2-2{\color{darkgray}bc}\,cos\,{\color{gray}\large\beta}}\)
\({\color{darkgray}a}^2={\color{darkgray} b}^2+ {\color{darkgray} c}^2-2 {\color{darkgray} bc}\,cos\, {\color{gray}\large\beta}\hspace{10pt}\left\{{\color{darkgray}b},{\color{darkgray}c}\textsf{も同様の過程で証明できる。}\right\}\)
中心角が\(90^{\circ}\)の余弦定理は\(cos90^{\circ}{\scriptsize\,=\,}0\) より、\(b^{\scriptsize 2}{\scriptsize\;=\;}a^{\scriptsize 2}{\scriptsize +}c^{\scriptsize 2}{\scriptsize -}2ac\cdot 0\)\(\small\hspace{10pt}\rightarrow\hspace{10pt}\)\(b^{\scriptsize 2}{\scriptsize\;=\;}a^{\scriptsize 2}{\scriptsize +}c^{\scriptsize 2}\) となり \(\href{https://showanojoe.com/template-math/trigonometric-function/three-squares-theorem/}{\color{teal}\textsf{三平方の定理}}\) に帰結する。下図参照。