数列の定義
数列とは、隣り合う数の間に、ある一定の規則性をもたせて配列 した数の列をいう。
\(\large a\tiny 1\) から \(\large a\scriptsize n\) までの実数の数列は、\(\{{\large a}{\scriptsize n}\}\) と表記する。各実数\(\large a\scriptsize i\) を\(\class{Boldfont}{\textsf{項}}\) といい、項の下添え字 \({i}\) を \(\class{Boldfont}{\textsf{数項}}({\small\textsf{配列番号}})\)という。\(\large a \scriptsize 1\) から \(\large a \scriptsize n\) までの項の数列を \({\,\class{Boldfont}{\textsf{項数}}\, n\, \textsf{の数列}\,}({\scriptsize\,=\,}\lbrace a{\tiny n}\rbrace)\) という。 数列の最初の項\((a{\tiny 1})\) を\(\class{Boldfont}{\textsf{初項 }}\) といい、数列の最後の項\((a{\tiny n})\) を \(\class{Boldfont}{\textsf{末項}}\) という。 数列の規則性は下図\(1\)の \(d\,{\small or} \,r, \,D\, {\small or}\,R\) である。\(d(\small D)\) は\(\class{Boldfont}{\textsf{公差}}\)、\(r(\small R)\) は\(\class{Boldfont}{\textsf{公比}}\) を表す。

等差数列
図\(1\)の \(d\,{\small or}\,r\) が差 \((\small\textsf{これを文字 $\class{Boldfont}{d}$ で表記し、 $\class{Boldfont}{\textsf{公差}}$ を表す })\)なら、その数列は \(\class{Boldfont}{\textsf{等差数列}}\) である。

\(\class{Boldfont}{\textsf{等差数列の一般項の公式}}\)
図2から
\({\large a\tiny i}-{\large a{\tiny (i-1)}}\) でその公差 \(d\) が求まる。
\(a{\scriptsize i}\)\((\)一意の項\((\small\textsf{課題とする項})\)より一つ後ろの項 \()\small\,-\,(\) 一意の項\()\)。
項数 \(\large a\tiny n\) の値を求めるには、\(\class{Boldfont}{{\large a\tiny n}={\large a}{\tiny 1}+{\small(n-1)}d}\) の 等差数列の一般項の公式 を使う。
下添え字の \(n\) は 末項の数項か任意の項の数項かを課題に応じて判断する必要がある。
任意の項が \(\large a{\tiny i}\) なら \(n\) に \(i\) を代入して \(\class{Boldfont}{{\large a\tiny i}={\large a}{\tiny 1}+{\small(i-1)}d}\) からその値を求める。
\(\scriptsize(n-1)\) とするのは、 項 \(a{\tiny 1}{\small\sim}a{\tiny n}\) より、公差 \(d\) の閾数が一つ少ない からである。
一般項とは \(\left\{{a{\tiny n}}\right\}\) を \(a{\tiny n}\) の等式で表記した各項の共通した構成\((\)これを漸化式という\()\)をいう。
任意の項 \(\large a{\tiny j}\)\((\)値を\(\small\alpha\)とする\()\) 、 \(\large a{\tiny l}\)\((\)値を\(\small\beta\)とする\()\) で \(\left\{{a{\tiny n}}\right\}\) の初項 \(\large a\tiny 1\)、公差\(d\)、\(\large a{\tiny o}\) の値を求めるには、一般項の公式に当てはめた \(\left\{\begin{array}{l} {\large a}{\tiny 1}{\scriptsize\,+\,}{\scriptsize(j-1)}d{\scriptsize\,=\,}\alpha \\ {\large a{\tiny 1}}{\scriptsize\,+\,}{\scriptsize(l-1)}{\normalsize d}{\scriptsize\,=\,}\beta\end{array}\right.\) の連立方程式\((\beta{\small\,-\,}\alpha)\) から 初項 \(\large a\tiny 1\)、公差 \(d\) の数値を求める。
後ろの項\(\beta\)から前の項\(\alpha\)を引く連立一次方程式。
\(\large a{\tiny o}\) の値は 上記の連立方程式から得られた初項 \(\large a\tiny 1\), 公差 \(d\) の数値を一般項の公式の \(n\) に \(o\) を当てはめた、 \({\large a{\tiny o}}{\scriptsize\,+\,}\small(o-1)d\) の式で得られる。
\(\class{Boldfont}{\textsf{等差数列の和の公式}}\)
等差数列の和とは、項数\(n\) の初項\(a{\tiny 1}\)から末項\(a{\tiny n}\) までをすべて足すことである。等差数列の和の公式は、
\(\class{Boldfont}{S{\tiny n}{\small\,=\,}{\small\displaystyle\frac{1}{2}}n(a{\tiny 1}+a{\tiny n})}\)
\(\class{Boldfont}{S{\tiny n}{\small\,=\,}{\small\displaystyle\frac{1}{2}}n\{2a+{\small(n-1)}d\}}\) \(\hspace{30pt}\) \(\{\)\(S{\tiny n}\) は 項数\((n\textsf{個})\)の等差数列の総和 を表す記号。\(\}\)
\({\color{gray}{\textsf{[事例]}}}\)
\(1\) から \(100\) までの和を求める。
まぁ、\(1\) から \(100\) まで愚直に足していく奇特な行為はなるべく避けたい。そこで 等差数列の和の公式 \(S{\tiny n}={\small\displaystyle\frac{1}{2}}n(a{\tiny 1}+a{\tiny n})\) を使う。まずは、和の公式をイメージしてみる。
\(2S{\tiny n}= \small{\left\{ \begin{array}{c c c c c}a{\tiny 1}&a{\tiny 1}+d&a{\tiny 1}+2d&\cdots&a{\tiny 1}+{\scriptsize(n-3)}d&a{\tiny 1}+{\scriptsize(n-2)}d&a{\tiny 1}+{\scriptsize(n-1)}d \\ +&+&+&+&+&+&+ \\ a{\tiny 1}+{\scriptsize(n-1)}d&a{\tiny 1}+{\scriptsize(n-2)}d&a{\tiny 1}+{\scriptsize(n-3)}d&\cdots&a{\tiny 1}+2d&a{\tiny 1}+d&a{\tiny 1} \end{array} \right\}}\)
\(\hspace{120pt}\Downarrow(\scriptsize\textsf{式変形して$S{\tiny n}$の等式にする} )\)
\(S{\tiny n}= \small{{\displaystyle\frac{1}{2}}\left\{ \begin{array}{c c c c c}a{\tiny 1}&a{\tiny 1}+d&a{\tiny 1}+2d&\cdots&a{\tiny 1}+{\scriptsize(n-3)}&a{\tiny 1}+{\scriptsize(n-2)}d&a{\tiny 1}+{\scriptsize(n-1)}d \\ +&+&+&+&+&+&+ \\ a{\tiny 1}+{\scriptsize(n-1)}d&a{\tiny 1}+{\scriptsize(n-2)}d&a{\tiny 1}+{\scriptsize(n-3)}d&\cdots&a{\tiny 1}+2d&a{\tiny 1}+d&a{\tiny 1} \end{array} \right\}}\)
要は元の数列\((\textsf{公差$1$})\)と、その逆順の数列\((\textsf{公差${\scriptsize -}1$})\)を足し合わせた値の半分\(({\scriptsize\displaystyle\frac{1}{2}})\) が数列の和となる。また、逆順の最初の項は\(a{\tiny n}\)なので、
\(\hspace{10pt}S{\tiny n}= \small{{\displaystyle\frac{1}{2}}\left\{ \begin{array}{c c c c c}a{\tiny 1}&a{\tiny 1}+d&a{\tiny 1}+2d&\cdots&a{\tiny 1}+{\scriptsize(n-3)}&a{\tiny 1}+{\scriptsize(n-2)}d&a{\tiny 1}+{\scriptsize(n-1)}d \\ +&+&+&+&+&+&+ \\ a{\tiny n}&a{\tiny n}\!-\!d&a{\tiny n}\!-\!2d&\cdots&a{\tiny n}\!-\!{\scriptsize(n-3)}d&a{\tiny n}\!-\!{\scriptsize(n-2)}d &a{\tiny n}\!-\!{\scriptsize(n-1)}d\end{array} \right\}}\)
と変形でき、\({\small\displaystyle\frac{1}{2}}n\) に上下対応する項の和をかければ \({\small\displaystyle\frac{1}{2}}n(a{\tiny 1}+a{\tiny n})\) の和の公式が成り立つ。
また、 \(a{\tiny n}\) に \(\href{#等差数列の一般項の公式}{\color{teal}\textsf{等差数列の一般項の公式}}\) \(\class{Boldfont}{{\large a{\tiny 1}}{\small\,+\,(n-1)}d}\) を代入すると、もう一つの和の公式 \(S{\tiny n}={\small\displaystyle\frac{1}{2}}n\{2a{\tiny 1}+{\small(n-1)}d\}\) が導出できる。
さて、\(1\) から \(100\) までの和は \(\class{Boldfont}{{S\tiny 100}{\small\,=\,}{\small\displaystyle\frac{1}{2}}\cdot 100\{2 \cdot 1+(100-1)\cdot 1}\}{\scriptsize\,=\,}5050{\color{#00ff7f}\checkmark}\) である。
等比数列

\(\class{Boldfont}{\textsf{等比数列の一般項の公式}}\)
図\(3\)の等比数列\({\{\large a{\tiny n}}\}\)から
\(\small\displaystyle\frac{\large a\tiny i}{\large a{\tiny (i-1)}}\) でその公比 \(\large r\) が求まる。 つまり \(\large a{\scriptsize i}\)\((\)ある任意の項 \()\small\,\div\, {\Large a}({\scriptsize i -1})\)\((\)その任意の項より一つ前の項\()\)。
任意の項 \(\large a\tiny i\) の値を求めるには、\(\class{Boldfont}{{\large a\tiny n}={\large a}{\tiny 1}{\large r}^{\small{n-1}}}\) の 等比数列の一般項の公式 を使う。
下添え字の \(n\) は 末項の数項か任意の項の数項かを課題に応じて判断する必要がある。
任意の項が \(\large a{\tiny i}\) なら \(n\) に \(i\) を代入して \(\class{Boldfont}{{\large a\tiny i}={\large a}{\tiny 1}{\large r}^{\small{i-1}}}\) からその値を求める。
\(\scriptsize(n-1)\) とするのは、 項 \(a{\tiny 1}{\small\sim}a{\tiny n}\) の項数より、公比 \(\large r\) の閾数\((\)図\(3\)の項と項を結ぶ ◡ の個数\()\)が一つ少ない からである。
一般項とは \(\left\{{a{\tiny n}}\right\}\) を \(a{\tiny n}\) の等式で表記した各項の共通した構成\((\)これを漸化式という\()\)をいう。
項 \(\large a{\tiny j}\)\((\)値を\(\small\alpha\)とする\()\) 、 \(\large a{\tiny l}\)\((\)値を\(\small\beta\)とする\()\) で \(\left\{{a{\tiny n}}\right\}\) の初項 \(\large a\tiny 1\)、公比\(\large r\)、\(\large a{\tiny o}\) の値を求めるには、\(a{\tiny j},\,a{\tiny l}\) を一般項の公式に当てはめた \(\left\{\begin{array}{l}\class{Boldfont}{{\large a}{\tiny 1}{\large r}^{\small{j-1}}}{\scriptsize\,=\,}\alpha \\ \class{Boldfont}{{\large a}{\tiny 1}{\large r}^{\small{l-1}}}{\scriptsize\,=\,}\beta\end{array}\right.\) の 連立方程式\((\)\(\scriptsize\displaystyle\frac{\beta}{\alpha}\)\()\) から 初項 \(\large a\tiny 1\)、公比 \(\large r\) の数値を求める。
後ろの
項\(\beta\)を前の項\(\alpha\)で割る連立一次方程式。
\(\large a{\tiny o}\) の値は 上記の連立方程式から得られた初項 \(\large a\tiny 1\), 公比 \(\large r\) の数値を一般項の公式の \(n\) に \(o\) を当てはめた、\(\class{Boldfont}{{\large a}{\tiny 1}{\large r}^{\small{o-1}}}\) の式で得られる。
\(\class{Boldfont}{\textsf{等比数列の和の公式}}\)
\({\large S}{\tiny n}{\small\;=\;}{\large a}{\tiny 1}\,{\small\displaystyle\frac{1-r^n}{1-r^\phantom{n}}}\)
初項 \(\large a{\tiny 1}\)、公比 \(\large r\) の 等比数列\(\left\{a{\tiny n}\right\}\) の和は
\(\large S{\tiny n}\)\({\small\;=\;}\left\{a{\tiny 1}{\scriptsize\;+\;}a{\tiny 1}r{\scriptsize\;+\;}a{\tiny 1}r^2{\scriptsize\;+\;}a{\tiny 1}r^3{\scriptsize\;+\;}\small\cdots\cdots{\scriptsize\;+\;}a{\tiny 1}r^{n-1}\right\}\) となる。これに 公比\(\large r\) を掛けると
\(\large r\cdot S{\tiny n}\)\({\small\;=\;}\left\{a{\tiny 1}r{\scriptsize\;+\;}a{\tiny 1}r^2{\scriptsize\;+\;}a{\tiny 1}r^3{\scriptsize\;+\;}\small\cdots\cdots{\scriptsize\;+\;}a{\tiny 1}r^{n-1}{\scriptsize\;+\;}a{\tiny 1}r^n\right\}\) となる。それで、それぞれの和の辺々の差の連立方程式をもとめる。
\(S{\tiny n}{\small\,-\,}r\cdot S{\tiny n}\)\({\small\hspace{10pt}=\hspace{10pt}}\underset{{\hspace{15pt}\Large a{\tiny 1}}{\hspace{204pt}{\small\;+\;}\Large a{\tiny 1}r^{n}}}{\begin{array}{l}\hspace{10pt}a{\tiny 1}{\enclose{horizontalstrike}{{\scriptsize\;+\;}a{\tiny 1}r{\scriptsize\;+\;}a{\tiny 1}r^2{\scriptsize\;+\;}a{\tiny 1}r^3{\scriptsize\;+\;}\small\cdots\cdots{\scriptsize\;+\;}a{\tiny 1}r^{n-1}}} \\[-20pt] {\small -)}\!\!\underline{\hspace{21pt}{\enclose{horizontalstrike}{a{\tiny 1}r{\scriptsize\;+\;}a{\tiny 1}r^2{\scriptsize\;+\;}a{\tiny 1}r^3{\scriptsize\;+\;}\small\cdots\cdots{\scriptsize\;+\;}a{\tiny 1}r^{n-1}}{\scriptsize\;+\;}a{\tiny 1}r^n}}\end{array}}\)
それで、\(S{\tiny n}{\small\,-\,}r\cdot S{\tiny n}\)\({\small\;=\;}\large a{\tiny 1}{\small\,-\,}a{\tiny 1}\,r^{\scriptsize n}\)\({\small\hspace{10pt}\rightarrow\hspace{10pt}}\)\(S{\tiny n}(1{\small\,-\,}r)\)\({\small\;=\;}\)\({\large a}{\tiny 1}({\small 1}{\small\,-\,}r^n)\)\({\small\hspace{10pt}\rightarrow\hspace{10pt}}\)\(S{\tiny n}{\small\;=\;} a{\tiny 1}\,{\scriptsize\displaystyle\frac{1-r^n}{1-r^\phantom{n}}}\)
また、\(r\cdot S{\tiny n}{\small\,-\,}S{\tiny n}\)\({\small\;=\;}a{\tiny 1}\,r^{\scriptsize n}{\small\,-\,}\large a{\tiny 1}\)\({\small\hspace{10pt}\rightarrow\hspace{10pt}}\)\(S{\tiny n}(r{\small\,-\,}1)\)\({\small\;=\;}\)\({\large a}{\tiny 1}({r^n}{\small\,-\,}1)\)\({\small\hspace{10pt}\rightarrow\hspace{10pt}}\)\(S{\tiny n}{\small\;=\;} a{\tiny 1}\,{\scriptsize\displaystyle\frac{r^n-1}{r^\phantom{n}-1}}\) でもいい。
\(\lbrace\)公式の形は変わるが、いずれにせよ \(S{\tiny n}\) の式として整合性はとれている。\(\rbrace\)
\({\Large{\large\varSigma}}\) シグマ について
\(\displaystyle\sum_{i{\small\,=\,}1}^n a{\tiny i}\)
この記号は、任意の項数\(i\) が \(1\) から \(n\) までの \({\large a}{\tiny i}\) の値が順に \(+\) されていく 和の省略記号\(\textsf{総和}\) を表している。\(\large a{\tiny i}\) の \(i\) に \(1\) を代入した \({\large a}{\tiny 1}\) は \(\{{\large a}{\tiny n}\}\) の初項の値となる。
\(\class{Boldfont}{{\large a}{\tiny i}}\)を\(\href{https://showanojoe.com/template-math/supplementary-material/factor/#整式}{\color{teal}\class{Boldfont}{\textsf{整式}}}\)で表した総和の式
\(\displaystyle\sum_{i{\small\,=\,}1}^{n} {\small C}{\small\;=\;}nC\)\(\hspace{25pt}\displaystyle\sum_{i{\small\,=\,}1}^{n} i{\small\;=\;}\small\displaystyle\frac{1}{2}n(1{\small\,+\,}n)\)\(\hspace{25pt}\displaystyle\sum_{i{\small\,=\,}1}^{n} i^{2}{\small\;=\;}\small\displaystyle\frac{n(n{\scriptsize +}1)(2n{\scriptsize +}1)}{6}\)
\(\small\displaystyle\sum_{i{\small\,=\,}1}^{n} {\small C}\) の \(C\) は定数なので、項の値に関係なく \(C\) が項数分足されていく総和
\(\small\displaystyle\sum_{i{\small\,=\,}1}^{n}{\small C}{\scriptsize\,=\,}C{\scriptsize\,+\,}C{\scriptsize\,+\,}C{\scriptsize\,+\,}{\scriptsize\,+\,}\cdots{\scriptsize\,+\,}C{\scriptsize\,=\,}nC\) になる。
\(\small\displaystyle\sum_{i{\small\,=\,}1}^{n} i\) の総和は \({\scriptsize\,=\,}1{\scriptsize\,+\,}2{\scriptsize\,+\,}3{\scriptsize\,+\,}{\scriptsize\,+\,}\cdots{\scriptsize\,+\,}n\) の公差 \(1\) の等差数列の和で \({\scriptsize\,=\,}{\scriptsize\displaystyle\frac{1}{2}}\small n(1{\small\,+\,}n)\) となる。
\(\displaystyle\sum_{i{\small\,=\,}1}^{n} i^{2}\) は証明が必要である。
第\(1\)項の和から第\(n\)項までの和の自然数の\(\href{https://showanojoe.com/template-math/supplementary-material/set/}{\color{teal}\textsf{集合}}\)を \(S{\scriptsize n}\)、第\(1\)項の和から第\(n\)項までの平方\((\)\(2\)乗\()\)の自然数の和の集合を \(S{\scriptsize n^{2}}\) とする。
\(\begin{array}{ c c c c c c c c }\phantom{a}&\small\textsf{第$1$項の和}&\small\textsf{第$2$項までの和}&\small\textsf{第$3$項までの和}&\small\textsf{第$4$項までの和}&\small\textsf{第$5$項までの和}&\small\textsf{第$6$項までの和}&\cdots&\small\textsf{第$n$項までの和}& \\ {\large S}{\scriptsize n}&(\,1&1+2&1+2+3&1+2+3+4&1+2+3+4+5&1+2+3+4+5+6&\cdots&{\small\displaystyle\frac{1}{2}}n(1+n)\,) \\ {\large S}{\scriptsize n^{2}}&(\,1&1+4&1+4+9&1+4+9+16&1+4+9+16+25&1+4+9+16+25+36&\cdots&?\,)\end{array}\)
で、\(S{\scriptsize n},\)\(S{\scriptsize n^{2}}\) のそれぞれに対応する項の比は
\(\scriptsize\displaystyle\frac{S{\scriptsize n^{2}}}{\!\!S{\scriptsize n}}\)\({\scriptsize\,=\,}\)\(\large\lbrace\)\(\scriptsize\displaystyle\frac{1}{1},\,\)\(\scriptsize\displaystyle\frac{5}{3},\,\)\(\scriptsize\displaystyle\frac{14}{6},\,\)\(\scriptsize\displaystyle\frac{30}{10},\,\)\(\scriptsize\displaystyle\frac{55}{15},\,\)\(\scriptsize\displaystyle\frac{91}{21},\,\cdots,\,\)\(\scriptsize\displaystyle\frac{?}{?}\)\(\large\rbrace\) となる。それで、集合 \(\scriptsize\displaystyle\frac{S{\scriptsize n^{2}}}{\!\!S{\scriptsize n}}\) の要素の内、\(\scriptsize\displaystyle\frac{5}{3}\) が通分の基準\((\)これより約分できない\()\)となるので各要素の分母を \(3\) に通分する。
\(\scriptsize\displaystyle\frac{S{\scriptsize n^{2}}}{\!\!S{\scriptsize n}}\)\({\scriptsize\,=\,}\)\(\large\lbrace\)\(\scriptsize\displaystyle\frac{3}{3},\,\)\(\scriptsize\displaystyle\frac{5}{3},\,\)\(\scriptsize\displaystyle\frac{7}{3},\,\)\(\scriptsize\displaystyle\frac{9}{3},\,\)\(\scriptsize\displaystyle\frac{11}{3},\,\)\(\scriptsize\displaystyle\frac{13}{3},\,\cdots,\,\)\(\scriptsize\displaystyle\frac{?}{?}\)\(\large\rbrace\) になる。これで要素の分子は奇数の整式 \(2n{\small\,\pm\,} 1\) の \(2n{\small\,+\,} 1\) になっていることがわかる。
以上から、自然数の平方の和 \(S{\scriptsize n^{2}}\) の規則性は \(\small\displaystyle\frac{2n{\scriptsize +}1}{3}\) なので、これを自然数の和にかける。自然数の和 \(S{\scriptsize n}\) は 初項\(1\)、公差\(1\)の等差数列なので、その和の公式にあてはめた \(\scriptsize\displaystyle\frac{1}{2}n(1{\small\,+\,}n)\) の式になる。
よって、\({\displaystyle\sum_{i{\small\,=\,}1}^{n}} i^{2}\)\({\small\;=\;}\small\displaystyle\frac{2n{\scriptsize +}1}{3}\)\(\times\)\(\small\displaystyle\frac{1}{2}n(1{\small\,+\,}n)\)\({\small\;=\;}\small\displaystyle\frac{n(n{\scriptsize +}1)(2n{\scriptsize +}1)}{6}{\color{#000}\checkmark}\)
階差数列を導く数列
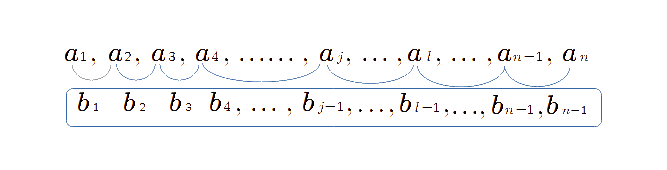
ある数列の任意の項 \(\large a{\tiny i}\) からその一つ前の項 \(\large a{\tiny i-1}\) を引いた値の項で構成される数列に関数\(\large f\)の規則性があれば、その数列は 階差数列 である。
図\(4\)では\(\left\{a{\tiny n}\right\}\)がある数列、仮称で \(\class{Boldfont}{\textsf{階差数列を導く数列}}(\textsf{関数列})\) としておこう。
そして、下段の \(\small\enclose{roundedbox}[mathcolor=darkblue]{\color{white}{aaaaa}}\) 内の数列 \(\left\{b{\tiny n-1}\right\}\) が階差数列である。まぁ、ややっこしい。
階差数列を導く数列の一般項の公式
\({\large a}{\tiny n}{\small\hspace{5pt}=\hspace{5pt}}{\large a}{\tiny 1}{\small\;+\;}\small\displaystyle\sum_{i=1}^{n-1}\!\large b{\tiny i}\)
\(\left(\small\displaystyle\sum_{i=2}^{n}\!\large a{\tiny i-1}{\scriptsize\hspace{5pt}=\hspace{5pt}}\small\displaystyle\sum_{i=1}^{n-1}\!\large b{\tiny i}\right)\)\({\small\hspace{20pt}\Rightarrow\hspace{20pt}}\)\(\small{\left\{ \begin{array}{c c c c c}a{\tiny 2}&{\scriptsize -}&a{\tiny 1}&{\scriptsize =}&b{\tiny 1} \\ & & {\small +} & & \\ a{\tiny 3}&{\scriptsize -}&a{\tiny 2}&{\scriptsize =}&b{\tiny 2} \\ & & {\small +} & & \\ a{\tiny 4}&{\scriptsize -}&a{\tiny 3}&{\scriptsize =}&b{\tiny 3} \\ & & {\small +} & & \\ a{\tiny 5}&{\scriptsize -}&a{\tiny 4}&{\scriptsize =}&b{\tiny 4}\\ & & {\small +} & & \\& &\vdots & & \\ & & {\small +} & & \\ a{\tiny n}&{\scriptsize -}&a{\tiny n-1}&{\scriptsize =}&b{\tiny n-1}\end{array} \right\}}\)\({\small\hspace{20pt}\Rightarrow\hspace{20pt}}\)\(\small{\left\{ \begin{array}{c c c c c}\color{lightgray}a{\tiny 2}&{\scriptsize -}&a{\tiny 1}&\color{lightgray}{\scriptsize =}&b{\tiny 1} \\ & & {\small +} & & \\ \color{lightgray}a{\tiny 3}&\color{lightgray}{\scriptsize -}&\color{lightgray}a{\tiny 2}&\color{lightgray}{\scriptsize =}&b{\tiny 2} \\ & & {\small +} & & \\ \color{lightgray}a{\tiny 4}&\color{lightgray}{\scriptsize -}&\color{lightgray}a{\tiny 3}&\color{lightgray}{\scriptsize =}&b{\tiny 3} \\ & & {\small +} & & \\ \color{lightgray}a{\tiny 5}&\color{lightgray}{\scriptsize -}&\color{lightgray}a{\tiny 4}&\color{lightgray}{\scriptsize =}&b{\tiny 4}\\ & & {\small +} & & \\& &\color{lightgray}\vdots & & \\ & & {\small +} & & \\ a{\tiny n}&\color{lightgray}{\scriptsize -}&\color{lightgray}a{\tiny n-1}&\color{lightgray}{\scriptsize =}&b{\tiny n-1}\end{array} \right\}}\)
\({\small\hspace{0pt}\Rightarrow\hspace{20pt}}{\small-\;}{\large a}{\tiny 1}{\small\;+\;}{\large a}{\tiny n}{\small\hspace{5pt}\rightarrow\hspace{5pt}}\small\displaystyle\sum_{i=1}^{n-1}\!\large b{\tiny i}\)
階差数列を導く数列 \(\left\{\large a{\tiny n}\right\}\) の 第\(i\)項\(\,-\,\)\(\textsf{第}{\small i-1}\)項の総和 \(\small\displaystyle\sum_{i=2}^{n}\large a{\tiny i-1}\) と \(\left\{\large a{\tiny n}\right\}\) の階差数列 \(\left\{\large b{\tiny n-1}\right\}\) の 各項の総和 \(\small\displaystyle\sum_{i=1}^{n-1}\large b{\tiny i}\) は等しい。
\(\small\hspace{10pt}\Rightarrow\hspace{10pt}\) それで、辺々加えた表にすると、\(\small\hspace{10pt}\Rightarrow\hspace{10pt}\) 同類項が処理されて、\(\small\hspace{10pt}\Rightarrow\hspace{10pt}\)\({\small-\;}{\large a}{\tiny 1}{\small\;+\;}{\large a}{\tiny n}{\small\hspace{5pt}\rightarrow\hspace{5pt}}\small\displaystyle\sum_{i=1}^{n-1}\!\large b{\tiny i}\) から階差数列を導く数列 \(\left\{\large a{\tiny n}\right\}\) の一般項の公式 \({\large a}{\tiny n}{\small\hspace{2pt}=\hspace{2pt}}{\large a}{\tiny 1}{\small\:+\:}\small\displaystyle\sum_{i=1}^{n-1}\!\large b{\tiny i}\) が導出される。
漸化式
漸化式とは、数列 \(\left\{\large a{\tiny n}\right\}\) の任意の項 \(\large a{\tiny i}\) と、それに隣接する項 \(\large a{\tiny i+1}\) または \(\large a{\tiny i-1}\) との間で成り立つ関係式を \(\large a{\tiny n+1}\) の等式に纏めた公式をいう。
等差数列
漸化式 \({\large a{\tiny n+1}}{\scriptsize\,=\,}{\large a{\tiny n}}{\scriptsize\,+\,}d\)\(\hspace{20pt}{\small\leftarrow}\hspace{5pt}\textsf{関係式}\;a{\tiny i+1}{\scriptsize\,-\,}a{\tiny i}{\scriptsize\,=\,}d\)
等比数列
漸化式 \({\large a{\tiny n+1}}{\scriptsize\,=\,}r{\large a{\tiny n}}\)\(\hspace{20pt}{\small\leftarrow}\hspace{5pt}\textsf{関係式}\;{\scriptsize\displaystyle\frac{a{\tiny i+1}}{a{\tiny i}}}{\scriptsize\,=\,}r\)
\(\class{Boldfont}{\textsf{階差数列を導く数列}}\)
漸化式 \({\large a{\tiny n+1}}{\scriptsize\,=\,}{\large a{\tiny n}}{\scriptsize\,+\,}{\large f{\scriptsize ({\small a}{\tiny{n}}\!-\!{\small a}{\tiny{n\!-\!1}})}}\)\(\hspace{20pt}{\small\leftarrow}\hspace{5pt}\textsf{関係式}\;{\large a{\tiny i}}{\scriptsize\,-\,}{\large a{\tiny i-1}}{\scriptsize\,=\,}{\large f{\scriptsize ({\small a}{\tiny{i}}\!-\!{\small a}{\tiny{i\!-\!1}})}}\)
数列の一般形
漸化式 \({\large a{\tiny n+1}}{\scriptsize\,=\,}p{\large a{\tiny n}}{\scriptsize\,+\,}q\)\(\hspace{20pt}(\textsf{$p,\,q$ は定数})\)
解法は、まず \(\large a\tiny n+1\) と \(\large a\tiny n\) を \(\alpha\) と置く。 \(\cdots\,?\)
はぁ~っ \(?\) 何のこっちゃ \(?\)\(\hspace{10pt}\) だよね。
何で違う項を同じ文字に置くんだぁ~っ ? って話だが、以下の解説メモで
漸化式 \({\large a{\tiny n+1}}{\scriptsize\,=\,}p{\large a{\tiny n}}{\scriptsize\,+\,}q\) の \({\large a\tiny n\!+\!1},\,{\large a\tiny n}\) を、ある変数 \(\alpha\) で引いた式に置き換えてみると
\({\large a\tiny n+1}{\scriptsize\,-\,}\alpha{\scriptsize\;=\;}p({\large a\tiny n}{\scriptsize\,-\,}\alpha)\)\({\scriptsize\hspace{10pt}\rightarrow\hspace{10pt}}\)\({\large a\tiny n+1}{\scriptsize\,-\,}\alpha{\scriptsize\;=\;}p{\large a\tiny n}{\scriptsize\,-\,}p\alpha\)
となりうる。
それで、左辺の \({\scriptsize\,-\,}\alpha\) を右辺に移項して
\({\large a\tiny n+1}{\scriptsize\;=\;}p{\large a\tiny n}{\scriptsize\,-\,}p\alpha{\scriptsize\,+\,}\alpha\)。
上式と漸化式を比較すると\(\hspace{10pt}\)\(\small\begin{array}{l}{\large a\tiny n+1}{\scriptsize\;=\;}p{\large a\tiny n}{\scriptsize\,-\,}p\alpha{\scriptsize\,+\,}\alpha \\ {\large a{\tiny n+1}}{\scriptsize\,=\,}p{\large a{\tiny n}}{\scriptsize\,+\,}q \end{array}\)\(\hspace{10pt}\)となり \(q{\scriptsize\;=\;}{\scriptsize -}p\alpha{\scriptsize +}\alpha\) であることがわかる。
それで、\(q{\scriptsize\;=\;}{\scriptsize -}p\alpha{\scriptsize\;+\;}\alpha\)\({\scriptsize\hspace{10pt}\rightarrow\hspace{10pt}}\)\(q{\scriptsize\;+\;}p\alpha{\scriptsize\;=\;}\alpha\)\({\scriptsize\hspace{10pt}\rightarrow\hspace{10pt}}\)\(\alpha{\scriptsize\;=\;}p\alpha{\scriptsize\,+\,}q\) と式変形してやると、\(p{\scriptsize\;=\;}1,\,\)\(q{\scriptsize\;=\;}0\) 以外の定数では適応できない方程式が導出される。
とりあえず、計算の過程で導出された、この整合性がとれない方程式\((\)特性方程式という\()\)と漸化式を比較してみると、
\(\begin{array}{l}\hspace{11pt}\alpha{\scriptsize\;=\;}p\alpha{\scriptsize\;+\;}q \\[-5pt] {\large a{\tiny n+1}}{\scriptsize\,=\,}p{\large a{\tiny n}}{\scriptsize\,+\,}q\end{array}\hspace{5pt}\)から \(\alpha{\scriptsize\;=\;}\large a\tiny n+1\)\(,\;\)\(\alpha{\scriptsize\;=\;}\large a\tiny n\) となる。
続けよう。
\(\large a\tiny n+1\) と \(\large a\tiny n\) を \(\alpha\) と置き、これを漸化式 \({\large a{\tiny n+1}}{\scriptsize\,=\,}p{\large a{\tiny n}}{\scriptsize\,+\,}q\) との連立方程式にかけると、
\(\underset{\hspace{10pt}\begin{array}{l}{\Large a}{\tiny n+1}{\small\,-\,}\alpha \hspace{5pt}\\[-10pt]\hspace{30pt}{\,=\,} p{\large a\tiny n}{\scriptsize\,-\,}p\alpha \end{array}}{\begin{array}{l}\hspace{15pt}{\large a{\tiny n+1}}{\scriptsize\,=\,}p{\large a{\tiny n}}{\scriptsize\,+\,}q\\[-10pt] {\small -\;)}\!\!\underline{\hspace{16pt}{{\alpha{\scriptsize\;=\;}p\alpha}{\scriptsize\;\;+\,}q}} \end{array}}\) \(\hspace{10pt}\)で、解説メモの漸化式に置き換えた式 \({\large a\tiny n+1}{\scriptsize\,-\,}\alpha{\scriptsize\;=\;}p({\large a\tiny n}{\scriptsize\,-\,}\alpha)\) となる。
これを式変形すると、\(\alpha{\small\,=\,}\small\displaystyle\frac{q}{1{\small\,-\,}p}\) で、 \(p\) と \(q\) の定数が定まると \(\alpha\) が求まる。
\(\color{gray}\textsf{[事例]}\)
\(\hspace{5pt}\textsf{初項}\,{\large a\tiny 1}{\small\,=\,}3\)、\(\textsf{漸化式が}\,{\large a\tiny n+1}{\small\,=\,}5{\large a\tiny n}{\small\,+\,}7\) の数列 \(\left\{\large a\tiny n\right\}\) の一般項を求めてみる。
