加法定理とその証明
加法定理とは、三角形の三辺の比を求める定理である。
加法定理の公式
\(\left\{\begin{array}{l}\href{#1}{\color{teal}{cos(\alpha{\small+}\beta)\,{\small =}\,cos{\large \alpha} \,cos\beta\,{\small -}\,sin{\large\alpha} \,sin\beta}} \\[3pt] \href{#2}{\color{teal}{cos(\alpha{\small-}\beta)\,{\small =}\,cos{\large \alpha} \,cos\beta\,{\small +}\,sin{\large\alpha} \,sin\beta}} \\[3pt] \href{#3}{\color{teal}{sin(\alpha{\,\small +\,}\beta){\,\small =\,}sin{\large\alpha} cos{\large\beta}{\,\small +\,}cos\alpha sin\beta}} \\[3pt] \href{#4}{\color{teal}{sin(\alpha{\,\small -\,}\beta){\,\small =\,}sin{\large\alpha} cos\beta{\,\small -\,}cos{\large\alpha} sin\beta}} \\[3pt] \href{#5}{\color{teal}{tan(\alpha{\,\small +\,}\beta){\,\small =\,}\small\displaystyle\frac{tan{\normalsize\alpha}{\,\scriptsize +\,}tan\beta}{1{\,\scriptsize -\,}tan{\normalsize\alpha}tan\beta}}} \\[3pt] \href{#5}{\color{teal}{tan(\alpha{\,\small -\,}\beta){\,\small =\,}\small\displaystyle\frac{tan{\normalsize\alpha}{\,\scriptsize -\,}tan\beta}{1{\,\scriptsize +\,}tan{\normalsize\alpha}tan\beta}}}\end{array}\right.\)
以下、証明。
\[cos(\alpha{\small+}\beta)\,{\small =}\,cos{\large \alpha} \,cos\beta\,{\small -}\,sin{\large\alpha} \,sin\beta\]
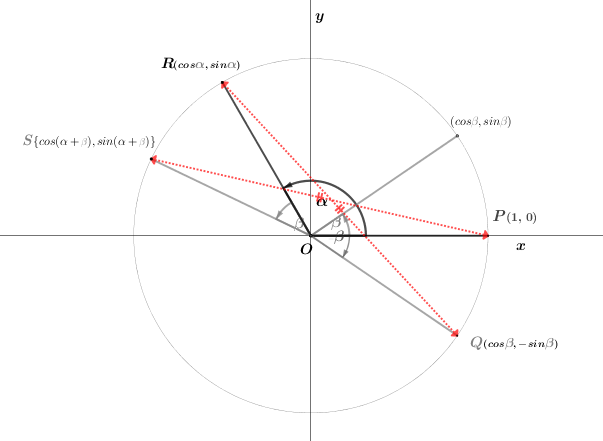
三平方の定理による座標上の二点間の距離\({\textcolor{gray}Q}R\)
\(({\textcolor{gray}Q}R)^2\left\{\begin{array}{l}\,{\small =}\,(cos\beta-cos\alpha)^2+(-sin\beta-sin\alpha)^2 \\ \,{\small =}\,cos^{2}\beta-2(cos\beta\,cos\alpha)+cos^{2}\alpha+\{sin^{2}\beta{\,\small +\,}2(sin\beta sin\alpha)+sin^{2}\alpha\} \\ \,{\small =}\,cos^{2}\alpha+sin^{2}\alpha+cos^{2}\beta+sin^{2}\beta-2(cos\alpha\,cos\beta){\,\small +\,}2(sin\alpha\,sin\beta) \\ \,{\small =}\,1+1-2(cos\alpha\,cos\beta-sin\alpha\,sin\beta) \\ \,{\small =}\,2-2(cos\alpha\,cos\beta-sin\alpha\,sin\beta) \end{array}\right.\)
三平方の定理による座標上の二点間の距離\(P{\textcolor{gray}S}\)
\((P{\textcolor{gray}S})^2\left\{\begin{array}{l}\,{\small =}\{1{\,\small -\,}cos(\alpha{\,\small +\,}\beta)\}^{2}+\{0{\,\small -\,}sin(\alpha{\,\small +\,}\beta)\}^{2} \\ 1-2\{cos(\alpha{\,\small +\,}\beta)\}+cos(\alpha{\,\small +\,}\beta)^{2}+sin(\alpha{\,\small +\,}\beta)^{2} \\ cos(\alpha{\,\small +\,}\beta)^{2}+sin(\alpha{\,\small +\,}\beta)^{2}+1-2\{cos(\alpha{\,\small +\,}\beta)\} \\ 1{\,\small +\,}1{\,\small -\,}2\{cos(\alpha{\,\small +\,}\beta)\} \end{array}\right.\)
\(\textsf{上記から}\left\{\begin{array}{l}2-2(cos\alpha\,cos\beta-sin\alpha\,sin\beta){\,\small =\,}2-2cos(\alpha{\,\small +\,}{\color{gray}\beta}) \\[5pt] {\,\small =\,} \class{Boldfont}{cos(\alpha{\,\small +\,}\beta){\,\small =\,}cos\alpha\,cos\beta-sin\alpha\,sin\beta} \end{array}\right.\)
\[cos(\alpha{\small-}\beta)\,{\small =}\,cos{\large \alpha} \,cos\beta\,{\small +}\,sin{\large\alpha} \,sin\beta\]
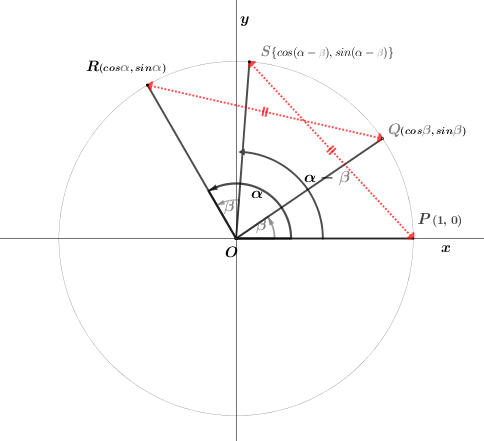
三平方の定理による座標上の二点間の距離\({\textcolor{gray}Q}R\)
\(({\textcolor{gray}Q}R)^2\left\{\begin{array}{l}\,{\small =}\,(cos\beta-cos\alpha)^2+(sin\beta-sin\alpha)^2 \\ \,{\small =}\,cos^{2}\beta-2(cos\beta\,cos\alpha)+cos^{2}\alpha+sin^{2}\beta-2(sin\beta sin\alpha)+sin^{2}\alpha \\ \,{\small =}\,cos^{2}\alpha+sin^{2}\beta+cos^{2}\beta+sin^{2}\beta-2(cos\alpha\,cos\beta)-2(sin\alpha\,sin\beta) \\ \,{\small =}\,1+1-2(cos\alpha\,cos\beta+sin\alpha\,sin\beta) \\ \,{\small =}\,2-2(cos\alpha\,cos\beta+sin\alpha\,sin\beta) \end{array}\right.\)
三平方の定理による座標上の二点間の距離\(P{\textcolor{gray}S}\)
\((P{\textcolor{gray}S})^2\left\{\begin{array}{l}\,{\small =}\{cos(\alpha-\beta)-1\}^{2}+\{sin(\alpha-\beta)-0\}^{2} \\ cos(\alpha-\beta)^{2}-2\{cos(\alpha-\beta)\}+1+sin(\alpha-\beta)^{2} \\ cos(\alpha-\beta)^{2}+sin(\alpha-\beta)^{2}+1-2\{cos(\alpha-\beta)\} \\ 2-2\{cos(\alpha-\beta)\} \end{array}\right.\)
\(\textsf{上記から}\left\{\begin{array}{l}2-2(cos\alpha\,cos\beta+sin\alpha\,sin\beta){\,\small =\,}2-2cos(\alpha-{\color{gray}\beta}) \\[5pt] {\,\small =\,} \class{Boldfont}{cos(\alpha-\beta){\small =}cos\alpha\,cos\beta+sin\alpha\,sin\beta} \end{array}\right.\)
\[sin(\alpha{\,\small +\,}\beta){\,\small =\,}sin{\large\alpha} cos{\large\beta}{\,\small +\,}cos\alpha sin\beta\]
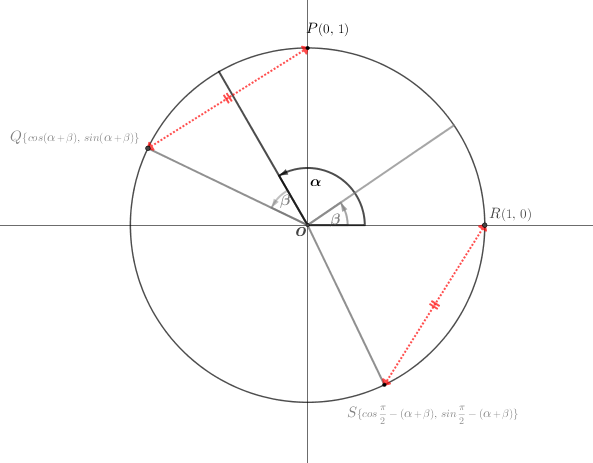
三平方の定理による座標上の二点間の距離\(P{\textcolor{gray}Q}\)
\((P{\textcolor{gray}Q})^{2}\left\{\begin{array}{l}{\,\small =\,}\{0-cos(\alpha+\beta)\}^{2}+\{1-sin(\alpha+\beta)\}^{2} \\
{\,\small =\,}cos^{2}(\alpha+\beta){\,\small +\,}1-2sin(\alpha+\beta)+{sin^{2}(\alpha+\beta)} \\ {\,\small =\,}cos^{2}(\alpha{\,\small +\,}\beta){\,\small +\,}sin^{2}(\alpha+\beta){\,\small +\,}1-2sin(\alpha{\,\small +\,}\beta) \\
{\,\small =\,}2-2sin(\alpha+\beta) \end{array}\right.\)
三平方の定理による座標上の二点間の距離\(R{\textcolor{gray}S}\)
\((R{\textcolor{gray}S})^{2}\left\{\begin{array}{l}{\,\small =\,}[1-cos\{\,{\small\displaystyle\frac{\pi}{2}}-(\alpha+\beta)\}]^{2}{\,\small +\,}[0-sin\{\,{\small\displaystyle\frac{\pi}{2}}-(\alpha+\beta)\}]^2 \hspace{10pt} ☜\hspace{5pt}\href{https://showanojoe.com/template-math/trigonometric-function/extension-trigonometric-ratios/#三角比の還元公式}{\color{teal}\small\textsf{三角比の還元公式}} \\
{\,\small =\,}1-2cos\{\,{\small\displaystyle\frac{\pi}{2}}-(\alpha+\beta)\}+cos^{2}\{\,{\small\displaystyle\frac{\pi}{2}}-(\alpha+\beta)\}+sin^{2}\{\,{\small\displaystyle\frac{\pi}{2}}-(\alpha+\beta)\} \\ {\,\small =\,}cos^{2}\{\,{\small\displaystyle\frac{\pi}{2}}-(\alpha+\beta)\}+sin^{2}\{\,{\small\displaystyle\frac{\pi}{2}}-(\alpha+\beta)\}{\,\small +\,}1-2cos\{\,{\small\displaystyle\frac{\pi}{2}}-(\alpha+\beta)\} \\
{\,\small =\,}2-2cos\{\,{\small\displaystyle\frac{\pi}{2}}-(\alpha+\beta)\}\end{array}\right.\)
\(\textsf{上記から}\left\{\begin{array}{l}{\,\small =\,}2-2sin(\alpha+\beta){\,\small =\,}2-2cos\{\,{\small\displaystyle\frac{\pi}{2}}-(\alpha+\beta)\} \\ {\,\small =\,}\class{Boldfont}{sin(\alpha+\beta)}{\,\small =\,}cos\{\,{\small\displaystyle\frac{\pi}{2}}-(\alpha+\beta)\} \\ {\,\small =\,}cos\{\,({\small\displaystyle\frac{\pi}{2}}-\alpha)-\beta\} {\,\small =\,}cos({\small\displaystyle\frac{\pi}{2}}-\alpha)cos\beta{\,\small +\,}sin({\small\displaystyle\frac{\pi}{2}}-\alpha)sin\beta \hspace{50pt}\{{\small\textsf{$\textsf{②}\,cos(\alpha{\small-}\beta)\,{\scriptsize =}\,cos{\large \alpha} \,cos\beta\,{\scriptsize +}\,sin{\large\alpha} \,sin\beta$ に該当。}}\} \\ \class{Boldfont}{{\,\small =\,}sin{\large\alpha} cos\beta{\,\small +\,}cos{\large\alpha} sin\beta} \end{array}\right.\)
\[sin(\alpha{\,\small -\,}\beta){\,\small =\,}sin{\large\alpha} cos\beta{\,\small -\,}cos{\large\alpha} sin\beta\]
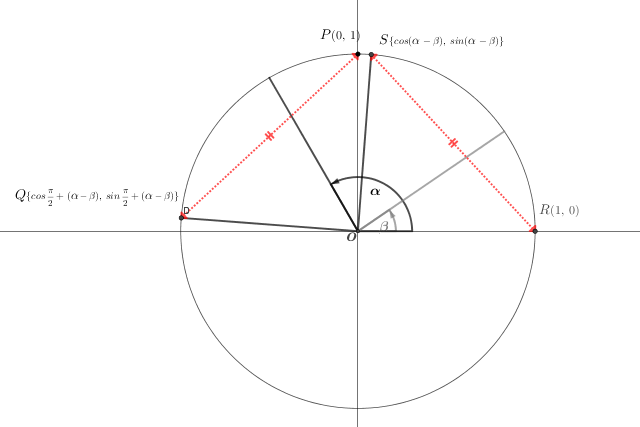
三平方の定理による座標上の二点間の距離\(PQ\)
\((PQ)^{2}\left\{\begin{array}{l}{\,\small =\,}\left[0-cos\{\,{\small\displaystyle\frac{\pi}{2}}{\,\small +\,}(\alpha-\beta)\}^{2}\right]+\left[1-sin\{\,{\small\displaystyle\frac{\pi}{2}}{\,\small +\,}(\alpha-\beta)\}^{2}\right] \\
{\,\small =\,}cos^{2}\{\,{\small\displaystyle\frac{\pi}{2}}{\,\small +\,}(\alpha-\beta)\}{\,\small +\,}1-2sin\{\,{\small\displaystyle\frac{\pi}{2}}{\,\small +\,}(\alpha-\beta)\}+sin^{2}\{\,{\small\displaystyle\frac{\pi}{2}}{\,\small +\,}(\alpha-\beta)\} \\ {\,\small =\,}cos^{2}\{\,{\small\displaystyle\frac{\pi}{2}}{\,\small +\,}(\alpha-\beta)\}+sin^{2}\{\,{\small\displaystyle\frac{\pi}{2}}{\,\small +\,}(\alpha-\beta)\}{\,\small +\,}1-2sin\{\,{\small\displaystyle\frac{\pi}{2}}{\,\small +\,}(\alpha-\beta)\} \\
{\,\small =\,}2-2sin\{\,{\small\displaystyle\frac{\pi}{2}}-(\alpha-\beta)\} \end{array}\right.\)
三平方の定理による座標上の二点間の距離\(RS\)
\((RS)^{2}\left\{\begin{array}{l}{\,\small =\,}\{0-cos(\alpha-\beta)\}^{2}+\{1-sin(\alpha-\beta)\}^{2} \\
{\,\small =\,}cos^{2}(\alpha-\beta){\,\small +\,}1-2sin(\alpha-\beta)+{sin^{2}(\alpha-\beta)} \\ {\,\small =\,}cos^{2}(\alpha{\,\small +\,}\beta){\,\small +\,}sin^{2}(\alpha-\beta){\,\small +\,}1-2sin(\alpha{\,\small +\,}\beta) \\
{\,\small =\,}2-2sin(\alpha-\beta) \end{array}\right.\)
\(\textsf{上記から}\left\{\begin{array}{l}{\,\small =\,}{\,\small =\,}2-2sin\{\,{\small\displaystyle\frac{\pi}{2}}{\,\small +\,}(\alpha-\beta)\}{\,\scriptsize =\,}2-2sin(\alpha-\beta) \\ {\,\small =\,}\class{Boldfont}{sin(\alpha-\beta)}{\,\small =\,}sin\{\,{\small\displaystyle\frac{\pi}{2}}{\,\small +\,}(\alpha-\beta)\} \\ {\,\small =\,}sin\{\,({\small\displaystyle\frac{\pi}{2}}{\,\small +\,}\alpha){\,\small +\,}(-\beta)\} {\,\small =\,}sin({\small\displaystyle\frac{\pi}{2}}{\,\small +\,}\alpha)cos(-\beta){\,\small +\,}cos({\small\displaystyle\frac{\pi}{2}}{\,\small +\,}\alpha)sin(-\beta)\hspace{50pt}\{{\small\textsf{$\textsf{③}\,sin(\alpha{\,\small +\,}\beta)\,{\scriptsize =}\,sin{\large \alpha} \,cos\beta\,{\scriptsize +}\,cos{\large\alpha} \,sin\beta$ に該当。}}\} \\ \class{Boldfont}{{\,\small =\,}sin{\large\alpha} cos\beta{\,\small -\,}cos{\large\alpha} sin\beta}\hspace{50pt}\left\{\small cos(-\beta){\scriptsize =}cos\beta,\hspace{10pt}sin(-\beta){\scriptsize =}-sin\beta \right\}\hspace{10pt} ☜\hspace{5pt}{\small\textsf{三角比の還元公式}}\end{array}\right.\)
以下、数式のみによる証明。
\(tan(\alpha{\,\small +\,}\beta)\left\{\begin{array}{l}{\,\small =\,}\small\displaystyle\frac{sin({\alpha}{\,\scriptsize +\,}\beta) }{cos(\alpha{\,\scriptsize +\,}\beta)} \\[5pt] {\,\small =\,}\small\displaystyle\frac{\scriptsize\displaystyle\frac{sin{\small\alpha}cos\beta{\,\scriptsize +\,}cos{\small\alpha}sin\beta)}{cos{\small\alpha}cos\beta}}{\scriptsize\displaystyle\frac{cos{\small\alpha}cos\beta{\,\scriptsize -\,}sin{\small\alpha}sin\beta)}{cos{\small\alpha}cos\beta}}\hspace{50pt}\{{\small\textsf{分母の項、分子の項をそれぞれ $tan$ か単位 $1$ にするために $cos{\normalsize\alpha}cos\beta$ で約分する。}}\} \\[5pt] {\,\small =\,}\small\displaystyle\frac{\scriptsize\displaystyle\frac{sin{\small\alpha}{\cancel{cos\beta}}}{cos{\small\alpha}{\cancel{cos\beta}}}{\,\scriptsize +\,}{\scriptsize\displaystyle\frac{{\cancel{cos{\small\alpha}}}sin\beta}{{\cancel{cos{\small\alpha}}}cos\beta}}}{\scriptsize\displaystyle\frac{{\cancel{cos{\small\alpha}cos\beta}}}{{\cancel{cos{\small\alpha}cos\beta}}}{\,\scriptsize -\,}{\scriptsize\displaystyle\frac{sin{\small\alpha}}{cos{\small\alpha}}}\,\cdot\,{\scriptsize\displaystyle\frac{sin\beta}{cos\beta}}} \\[5pt] \class{Boldfont}{{\,\small =\,}\small\displaystyle\frac{tan{\normalsize\alpha}{\,\scriptsize +\,}tan\beta}{1{\,\scriptsize -\,}tan{\normalsize\alpha}tan\beta}} \end{array}\right.\)
\(tan(\alpha{\,\small -\,}\beta)\left\{\begin{array}{l}{\,\small =\,}\small\displaystyle\frac{sin({\alpha}{\,\scriptsize -\,}\beta) }{cos(\alpha{\,\scriptsize -\,}\beta)} \\[5pt] {\,\small =\,}\small\displaystyle\frac{\scriptsize\displaystyle\frac{sin{\small\alpha}cos\beta{\,\scriptsize -\,}cos{\small\alpha}sin\beta)}{cos{\small\alpha}cos\beta}}{\scriptsize\displaystyle\frac{cos{\small\alpha}cos\beta{\,\scriptsize +\,}sin{\small\alpha}sin\beta)}{cos{\small\alpha}cos\beta}} \\[5pt] {\,\small =\,}\small\displaystyle\frac{\scriptsize\displaystyle\frac{sin{\small\alpha}{\cancel{cos\beta}}}{cos{\small\alpha}{\cancel{cos\beta}}}{\,\scriptsize -\,}{\scriptsize\displaystyle\frac{{\cancel{cos{\small\alpha}}}sin\beta}{{\cancel{cos{\small\alpha}}}cos\beta}}}{\scriptsize\displaystyle\frac{{\cancel{cos{\small\alpha}cos\beta}}}{{\cancel{cos{\small\alpha}cos\beta}}}{\,\scriptsize +\,}{\scriptsize\displaystyle\frac{sin{\small\alpha}}{cos{\small\alpha}}}\,\cdot\,{\scriptsize\displaystyle\frac{sin\beta}{cos\beta}}} \\[5pt] \class{Boldfont}{{\,\small =\,}\small\displaystyle\frac{tan{\normalsize\alpha}{\,\scriptsize -\,}tan\beta}{1{\,\scriptsize +\,}tan{\normalsize\alpha}tan\beta}} \end{array}\right.\)
加法定理から\(2\)倍角の公式
\[\class{Boldfont}{2\textsf{倍角の公式}}\]
\(\hspace{-25pt}\left.\begin{array}{l}cos2{\large\alpha}{\small\,=\,}cos^{2}{\large\alpha}{\small\,-\,}sin^{2}{\large\alpha}\hspace{3pt}\left\{\begin{array}{l}\small\textsf{角度変数は同角となる。${\normalsize\alpha}{\scriptsize\,=\,}{\normalsize\beta}$} \\ \small\textsf{加法定理より、 $cos({\normalsize\alpha{\scriptsize\,+\,}\beta}){\scriptsize\,=\,}cos{\normalsize\alpha}\,cos{\normalsize\beta}{\scriptsize\,-\,}sin{\normalsize\alpha}\,sin{\normalsize\beta}$ を適用。} \\ \hspace{10pt}\small\textsf{$\,\rightarrow\,cos({\normalsize\alpha{\scriptsize\,+\,}\alpha}){\scriptsize\,=\,}cos{\normalsize\alpha}\,cos{\normalsize\alpha}{\scriptsize\,-\,}sin{\normalsize\alpha}\,sin{\normalsize\alpha}$} \\ \hspace{20pt}\small\textsf{$\,\rightarrow\,cos2({\normalsize\alpha}){\scriptsize\,=\,}\underline{cos^{2}{\normalsize\alpha}{\scriptsize\,-\,}\,sin^{2}{\normalsize\alpha}}$} \\ \hspace{75pt}\small\textsf{${\scriptsize\,=\,}2cos^{2}{\normalsize\alpha}{\scriptsize\,-\,}(sin^{2}{\normalsize\alpha}{\small\,+\,}cos^{2}{\normalsize\alpha})$} \\ \hspace{63pt}\small\textsf{${\scriptsize\,=\,}\underline{2cos^{2}{\normalsize\alpha}{\scriptsize\,-\,}1}$} \\ \hspace{63pt}\small\textsf{${\scriptsize\,=\,}(sin^{2}{\normalsize\alpha}{\small\,+\,}cos^{2}{\normalsize\alpha}){\scriptsize\,-\,}2sin^{2}{\normalsize\alpha}$} \\ \hspace{63pt}\small\textsf{${\scriptsize\,=\,}\underline{1{\scriptsize\,-\,}2sin^{2}{\normalsize\alpha}}$}\end{array}\right\} \\[7pt] sin2{\large\alpha}{\small\,=\,}2sin{\large\alpha}\,cos{\large\alpha}\hspace{13pt}\left\{\begin{array}{l}\small\textsf{加法定理より、$sin({\normalsize\alpha{\scriptsize\,+\,}\beta}){\scriptsize\,=\,}sin{\normalsize\alpha}\,cos{\normalsize\beta}{\scriptsize\,+\,}cos{\normalsize\alpha}\,sin{\normalsize\beta}$ を適用。} \\ \hspace{10pt}\small\textsf{$\,\rightarrow\,sin({\normalsize\alpha{\scriptsize\,+\,}\alpha}){\scriptsize\,=\,}sin{\normalsize\alpha}\,cos{\normalsize\alpha}{\scriptsize\,+\,}cos{\normalsize\alpha}\,sin{\normalsize\alpha}$} \\ \hspace{20pt}\small\textsf{$\,\rightarrow\,sin2({\normalsize\alpha}) \\ {\scriptsize\,=\,}\underline{2sin{\normalsize\alpha}cos{\normalsize\alpha}}$} \end{array}\right\} \\[5pt] tan2{\large\alpha}{\small\,=\,}\small\displaystyle\frac{2tan{\normalsize\alpha}}{1-tan^{2}\normalsize\alpha}\hspace{26pt}\left\{\begin{array}{l}\small\textsf{三角比の相互関係式から、$tan{\normalsize\alpha}{\scriptsize\,=\,}\scriptsize\displaystyle\frac{sin{\small\alpha}}{cos{\small\alpha}}$} \\ \hspace{10pt}\small\textsf{$2$倍角の公式 から、$cos2{\normalsize\alpha}{\scriptsize\,=\,}cos^{2}{\normalsize\alpha}{\scriptsize\,-\,}sin^{2}{\normalsize\alpha},\,sin2{\normalsize\alpha}{\scriptsize\,=\,}2sin{\normalsize\alpha}2sin{\normalsize\alpha}$ を適用} \\ \hspace{20pt}\small\textsf{すると、$tan2{\normalsize\alpha}{\scriptsize\,=\,}\scriptsize\displaystyle\frac{sin2{\small\alpha}}{cos2{\small\alpha}}{\scriptsize\,=\,}\scriptsize\displaystyle\frac{2sin{\small\alpha}2cos{\small\alpha}}{cos^{2}{\small\alpha}{\tiny\,-\,}sin^{2}{\small\alpha}}$} \\ \hspace{10pt}\small\textsf{‘$1$’、すなわち$\left(\tiny\displaystyle\frac{\displaystyle\frac{1}{cos^{2}{\alpha}}}{\displaystyle\frac{1}{cos^{2}{\alpha}}}\right)$をかけて$\scriptsize\displaystyle\frac{2sin{\small\alpha}2cos{\small\alpha}}{cos^{2}{\small\alpha}{\tiny\,-\,}sin^{2}{\small\alpha}}\cdot \tiny\displaystyle\frac{\displaystyle\frac{1}{cos^{2}{\alpha}}}{\displaystyle\frac{1}{cos^{2}{\alpha}}}$ とし、$tan$ を導く。} \\ \hspace{10pt}\small\textsf{$\scriptsize\displaystyle\frac{2sin{\small\alpha}2cos{\small\alpha}}{cos^{2}{\small\alpha}{\tiny\,-\,}sin^{2}{\small\alpha}}\cdot \tiny\displaystyle\frac{\displaystyle\frac{1}{cos^{2}{\alpha}}}{\displaystyle\frac{1}{cos^{2}{\alpha}}}{\scriptsize\,=\,}\scriptsize\displaystyle\frac{2\displaystyle\frac{sin\alpha}{cos{\alpha}}}{1-\displaystyle\frac{sin^{2}\alpha}{cos^{2}{\alpha}}}{\small\,=\,}\underline{\scriptsize\displaystyle\frac{2tan{\small\alpha}}{1-tan^{2}\small\alpha}}$}\end{array}\right\}\end{array}\right.\)
\(2\)倍角の公式から半角の公式
半角の公式
\(\hspace{-25pt}\left.\begin{array}{l}cos^{2}\,{\scriptsize\displaystyle\frac{1}{2}}{\large\alpha}{\small\,=\,}{\scriptsize\displaystyle\frac{1{\scriptsize\,+\,}cos{\small\alpha}}{2}}\hspace{5pt}\left\{\begin{array}{l}\small\textsf{三角比の計算式に ‘$1$’ が出現したら、三角比の相互関係式 $1{\scriptsize\,=\,}cos^{2}{\normalsize\alpha}{\scriptsize\,+\,}sin^{2}{\normalsize\alpha}$ を考慮してみる。} \\ \small\textsf{$2$倍角の公式 $cos2{\normalsize\alpha}{\scriptsize\,=\,}cos^{2}{\normalsize\alpha}{\scriptsize\,-\,}sin^{2}{\normalsize\alpha}$ を適用。} \\ \hspace{10pt}\small\textsf{$\,\rightarrow\,{\color{black}\underline{\color{black}{cos2{\normalsize\alpha}}}}{\scriptsize\,=\,}cos^{2}{\normalsize\alpha}{\scriptsize\,-\,}sin^{2}{\normalsize\alpha}{\scriptsize\,=\,}2cos^{2}{\normalsize\alpha}{\scriptsize\,-\,}(cos^{2}{\normalsize\alpha}{\scriptsize\,+\,}sin^{2}{\normalsize\alpha}){\scriptsize\,=\,}\color{black}\underline{\color{black}2cos^{2}{\normalsize\alpha}{\scriptsize\,-\,}1}$} \\ \hspace{20pt}\small\textsf{$\,\rightarrow\,{{{cos2{\normalsize\alpha}}}}{\scriptsize\,=\,}{2cos^{2}{\normalsize\alpha}{\scriptsize\,-\,}1},\,{2cos^{2}{\normalsize\alpha}}{\scriptsize\,=\,}{1{\scriptsize\,+\,}cos2{\normalsize\alpha}},\,cos^{2}{\normalsize\alpha}{\scriptsize\,=\,}\scriptsize\displaystyle\frac{1+cos2{\small\alpha}}{2}$} \\ \small\textsf{$\normalsize\alpha$の半角なので、$\alpha$に${\scriptsize\displaystyle\frac{1}{2}}$を掛けると、$cos^{2}\,{\scriptsize\displaystyle\frac{1}{2}}{\alpha}{\small\,=\,}{\scriptsize\displaystyle\frac{1{\scriptsize\,+\,}cos{\small\alpha}}{2}}$} \end{array}\right\} \\[10pt] sin^{2}\,{\scriptsize\displaystyle\frac{1}{2}}{\large\alpha}{\small\,=\,}\scriptsize\displaystyle\frac{1{\scriptsize\,-\,}cos{\small\alpha}}{2}\hspace{10pt}\left\{\begin{array}{l}\small\textsf{これも$2$倍角の公式 $cos2{\normalsize\alpha}{\scriptsize\,=\,}cos^{2}{\normalsize\alpha}{\scriptsize\,-\,}sin^{2}{\normalsize\alpha}$ を適用。} \\ \hspace{10pt}\small\textsf{$\,\rightarrow\,{\color{black}\underline{\color{black}{cos2{\normalsize\alpha}}}}{\scriptsize\,=\,}cos^{2}{\normalsize\alpha}{\scriptsize\,-\,}sin^{2}{\normalsize\alpha}{\scriptsize\,=\,}(cos^{2}{\normalsize\alpha}{\scriptsize\,+\,}sin^{2}{\normalsize\alpha}){\scriptsize\,-\,}2sin^{2}{\normalsize\alpha}{\scriptsize\,=\,}\color{black}\underline{\color{black}1{\scriptsize\,-\,}2sin^{2}{\normalsize\alpha}}$} \\ \hspace{20pt}\small\textsf{$\,\rightarrow\,{{{cos2{\normalsize\alpha}}}}{\scriptsize\,=\,}{1{\scriptsize\,-\,}2sin^{2}{\normalsize\alpha}},\,{2sin^{2}{\normalsize\alpha}}{\scriptsize\,=\,}{1{\scriptsize\,-\,}cos2{\normalsize\alpha}},\,sin^{2}{\normalsize\alpha}{\scriptsize\,=\,}\scriptsize\displaystyle\frac{1-cos2{\small\alpha}}{2}$} \\ \small\textsf{$\normalsize\alpha$の半角なので、$\alpha$に${\scriptsize\displaystyle\frac{1}{2}}$を掛けると、$sin^{2}\,{\scriptsize\displaystyle\frac{1}{2}}{\alpha}{\small\,=\,}{\scriptsize\displaystyle\frac{1{\scriptsize\,-\,}cos{\small\alpha}}{2}}$} \end{array}\right\} \\[10pt] tan^{2}\,{\scriptsize\displaystyle\frac{1}{2}}{\large\alpha}{\small\,=\,}\scriptsize\displaystyle\frac{1{\scriptsize\,-\,}cos{\small\alpha}}{1{\scriptsize\,+\,}cos{\small\alpha}}\hspace{10pt}\left\{\begin{array}{l}\small\textsf{$\href{https://showanojoe.com/template-math/trigonometric-function/extension-trigonometric-ratios/#三角比の相互関係式}{\color{teal}\textsf{三角比の相互関係式}}$より、$tan{\alpha}{\small\,=\,}\scriptsize\displaystyle\frac{sin{\small\alpha}}{cos{\small\alpha}}$ なので、$tan^{2}{\scriptsize\displaystyle\frac{1}{2}}\alpha{\small\,=\,}\scriptsize\displaystyle\frac{sin^{\tiny 2}{\tiny\displaystyle\frac{1}{2}}{\small\alpha}}{cos^{\tiny 2}{\tiny\displaystyle\frac{1}{2}}{\small\alpha}}$} \\ \hspace{10pt}\small{\,\rightarrow\,tan^{2}{\scriptsize\displaystyle\frac{1}{2}}\alpha{\small\;=\;}\displaystyle\frac{\tiny\displaystyle\frac{1{\,-\,}cos{\scriptsize\alpha}}{2}}{\tiny\displaystyle\frac{1{\,+\,}cos{\scriptsize\alpha}}{2}}}{\small\;=\;}{\scriptsize\displaystyle\frac{2(1-cos\alpha)}{2(1+cos\alpha)}}\end{array}\right\} \end{array}\right.\)
\(2\)倍角の公式から\(3\)倍角の公式
\[\class{Boldfont}{3\textsf{倍角の公式}}\]
\(\begin{array}{l}sin3{\large\alpha}{\small\;=\;}3sin{\large\alpha}{\small\,-\,}4sin^{3}{\large\alpha}\left\{\small\begin{array}{l}\small{\scriptsize\;=\;}sin({\normalsize\alpha}{\scriptsize\;+\;}2{\normalsize\alpha}){\scriptsize\;=\;}sin{\normalsize\alpha}cos2{\normalsize\alpha}{\scriptsize\;+\;}cos{\normalsize\alpha}sin2{\normalsize\alpha} \\ \{\;\textsf{$\href{#加法定理の公式}{\color{teal}\textsf{加法定理の公式}}\;sin({\normalsize\alpha}{\,\scriptsize +\,}\beta){\,\scriptsize =\,}sin{\normalsize\alpha} cos{\normalsize\beta}{\,\scriptsize +\,}cos{\normalsize\alpha} sin{\normalsize\beta}$}\} \\[10pt] {\scriptsize\;=\;}sin{\normalsize\alpha}(1-2sin^{2}{\normalsize\alpha}){\scriptsize\;+\;}cos{\normalsize\alpha}\,{2sin{\normalsize\alpha cos{\normalsize\alpha}}} \\ \left\{\;\textsf{$\href{#2倍角の公式}{\color{teal}\textsf{$2$倍角の公式}}\;\begin{array}{l}\scriptsize cos2{\small\alpha}{\,\scriptsize =\,}1{\,\scriptsize -\,}2sin^{2}{\small\alpha} \\[-5pt] \scriptsize sin2{\small\alpha}{\scriptsize\;=\;}2sin{\small\alpha}cos{\small\alpha}\end{array}$}\right\} \\[10pt] {\scriptsize\;=\;}sin{\normalsize\alpha}(1-2sin^{2}{\normalsize\alpha}){\scriptsize\;+\;}2sin{\normalsize\alpha}\,(1-sin^{2}{\normalsize\alpha}) \\ \left\{\begin{array}{l}\textsf{$\href{https://showanojoe.com/template-math/trigonometric-function/extension-trigonometric-ratios/#三角比の相互関係式}{\color{teal}\textsf{三角比の相互関係式}}$の式変形} \\[-5pt] \scriptsize sin^{2}{\small\alpha}{\scriptsize\;+\;}cos^{2}{\small\alpha}{\scriptsize\;=\;}1\;{\scriptsize\rightarrow}\;cos^{2}{\small\alpha}{\scriptsize\;=\;}1{\scriptsize\;-\;}sin^{2}{\small\alpha} \end{array}\right\} \\[5pt] {\scriptsize\;=\;}sin{\normalsize\alpha}-2sin^{3}{\normalsize\alpha}{\scriptsize\;+\;}2sin{\normalsize\alpha}-2sin^{3}{\normalsize\alpha} \\ \{\textsf{と展開して}\} \\[10pt] {\small\;=\;}3sin{\large\alpha}{\small\,-\,}4sin^{3}{\large\alpha}\end{array}\right.\end{array}\)
\(\begin{array}{l}cos3{\large\alpha}{\small\;=\;}4cos^{3}{\large\alpha}{\small\,-\,}3cos{\large\alpha}\left\{\small\begin{array}{l}\small{\scriptsize\;=\;}cos({\normalsize\alpha}{\scriptsize\;+\;}2{\normalsize\alpha}){\scriptsize\;=\;}cos{\normalsize\alpha}cos2{\normalsize\alpha}{\scriptsize\;+\;}sin{\normalsize\alpha}sin2{\normalsize\alpha} \\ \{\;\textsf{$\href{#加法定理の公式}{\color{teal}\textsf{加法定理の公式}}\;cos({\normalsize\alpha}{\,\scriptsize +\,}\beta){\,\scriptsize =\,}cos{\normalsize\alpha} cos{\normalsize\beta}{\,\scriptsize +\,}sin{\normalsize\alpha} sin{\normalsize\beta}$}\} \\[10pt] {\scriptsize\;=\;}cos{\normalsize\alpha}(2cos^{2}{\normalsize\alpha}-1){\scriptsize\;-\;}sin{\normalsize\alpha}\,{2sin{\normalsize\alpha cos{\normalsize\alpha}}} \\ \left\{\;\textsf{$\href{#2倍角の公式}{\color{teal}\textsf{$2$倍角の公式}}\;\begin{array}{l}\scriptsize cos2{\small\alpha}{\,\scriptsize =\,}2cos^{2}{\small\alpha}-1 \\[-5pt] \scriptsize sin2{\small\alpha}{\scriptsize\;=\;}2sin{\small\alpha}cos{\small\alpha}\end{array}$}\right\} \\[10pt] {\scriptsize\;=\;}cos{\normalsize\alpha}(2cos^{2}{\normalsize\alpha}-1){\scriptsize\;-\;}2(1-cos^{2}{\normalsize\alpha})cos{\small\alpha} \\ \left\{\begin{array}{l}\textsf{$\href{https://showanojoe.com/template-math/trigonometric-function/extension-trigonometric-ratios/#三角比の相互関係式}{\color{teal}\textsf{三角比の相互関係式}}$の式変形} \\[-5pt] \scriptsize sin^{2}{\small\alpha}{\scriptsize\;+\;}cos^{2}{\small\alpha}{\scriptsize\;=\;}1\;{\scriptsize\rightarrow}\;sin^{2}{\small\alpha}{\scriptsize\;=\;}1{\scriptsize\;-\;}cos^{2}{\small\alpha} \end{array}\right\} \\[10pt]{\scriptsize\;=\;}cos{\normalsize\alpha}(2cos^{2}{\normalsize\alpha}-1){\scriptsize\;-\;}2cos{\normalsize\alpha}(1-cos^{2}{\normalsize\alpha}) \\ \{\textsf{と式を整理して}\} \\[10pt] 2cos^{3}{\normalsize\alpha}{\scriptsize\;-\;}cos{\small\alpha}{\scriptsize\;-\;}2cos{\normalsize\alpha}{\small\;+\;}2cos^{3}{\normalsize\alpha} \\ \{\textsf{と展開して}\} \\[10pt] {\small\;=\;}4cos^{3}{\normalsize\alpha}{\small\,-\,}3cos{\normalsize\alpha}\end{array}\right.\end{array}\)
\(\begin{array}{l}tan3{\large\alpha}{\small\;=\;}{\small\displaystyle\frac{3tan{\normalsize\alpha}-tan^{3}{\normalsize\alpha}}{1-3tan^{2}{\normalsize\alpha}}}\left\{\small\begin{array}{l}\small{\scriptsize\;=\;}tan({\normalsize\alpha}{\scriptsize\;+\;}2{\normalsize\alpha}){\scriptsize\;=\;}{\scriptsize\displaystyle\frac{tan{\small\alpha}+tan2{\small\alpha}}{1-tan{\small\alpha}tan2{\small\alpha}}} \\ \left\{\;\textsf{$\href{#加法定理の公式}{\color{teal}\textsf{加法定理の公式}}\;tan({\normalsize\alpha}{\,\scriptsize +\,}\beta){\,\scriptsize =\,}{\scriptsize\displaystyle\frac{tan{\small\alpha}+tan{\small\beta}}{1-tan{\small\alpha}tan{\small\beta}}}$}\right\} \\[10pt] {\scriptsize\;=\;}{\scriptsize\displaystyle\frac{tan{\small\alpha}+{\tiny\displaystyle\frac{2tan{\scriptsize\alpha}}{1-tan^{2}{\scriptsize\alpha}}}}{1-tan{\small\alpha}\,{\tiny\displaystyle\frac{2tan{\scriptsize\alpha}}{1-tan^{2}{\scriptsize\alpha}}}}} \\ \left\{\;\textsf{$\href{#2倍角の公式}{\color{teal}\textsf{$2$倍角の公式}}\;tan2{\small\alpha}{\scriptsize\;=\;}\scriptsize\displaystyle\frac{2tan{\small\alpha}}{1-tan^{2}{\small\alpha}}$}\right\} \\[10pt] {\scriptsize\;=\;}{\scriptsize\displaystyle\frac{tan{\small\alpha}(1-tan^{2}{\small\alpha})+2tan{\small\alpha}}{(1-tan^{2}{\small\alpha})\cdot 1-tan{\small\alpha}2tan{\small\alpha}}} \\ \left\{\begin{array}{l}\textsf{分子の両辺と分母の両辺に、} \\[-5pt] \textsf{$\scriptsize\,(1-tan^{2}{\small\alpha})\,$を掛けて分数式を簡略化する。} \end{array}\right\} \\[10pt]{\scriptsize\;=\;}{\scriptsize\displaystyle\frac{tan{\small\alpha}-tan^{3}{\small\alpha}+2tan{\small\alpha}}{1-tan^{2}{\small\alpha}-tan{\small\alpha}2tan{\small\alpha}}} \\ \{\textsf{と分母分子を展開して}\} \\[10pt] {\scriptsize\;=\;}{\scriptsize\displaystyle\frac{tan{\small\alpha}-tan^{2}{\small\alpha}+2tan{\small\alpha}}{1-tan^{2}{\small\alpha}-2tan^{2}{\small\alpha}}} \\ \{\textsf{と式の分母を整理すると、}\} \\[10pt] {\small\;=\;}{\scriptsize\displaystyle\frac{3tan{\small\alpha}-tan^{3}{\small\alpha}}{1-3tan^{2}{\small\alpha}}}\end{array}\right.\end{array}\)
