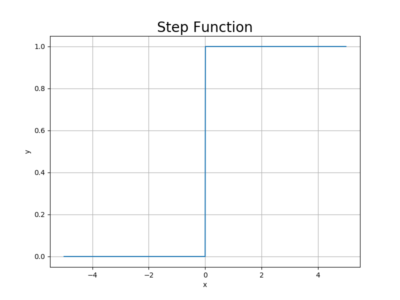
単純パーセプトロン
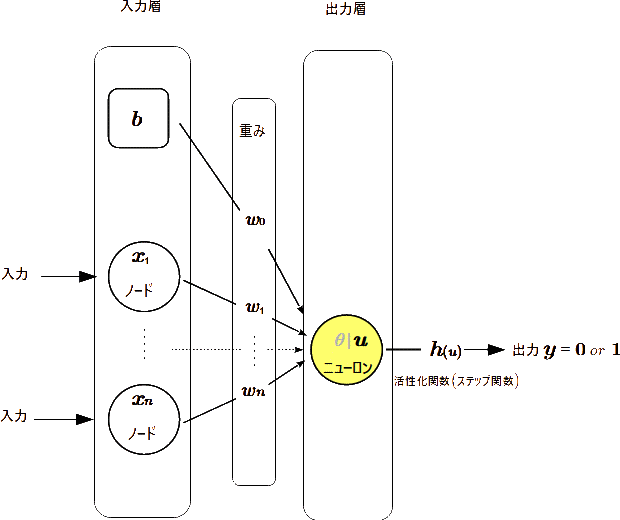
\(\textsf{図$1$から}\left\{\begin{array}{l}\textsf{単純パーセプトロン は 入力層( $x{\tiny 1},\,\cdots,\,x{\tiny n}$)ノード と 出力層( $u\:$)ニューロン の$2$層のみからなる。} \\[5pt] \textsf{入力値$X({x}{\tiny 1},\,\cdots,\,{x}{\tiny n})$ と 重み$W(w{\tiny 1},\,\cdots,\,w{\tiny n})$ を掛け合わせた値が 出力層で しきい値 $\theta$ 以下かそれよりか大きい} \\ \hspace{8pt}\textsf{かの値 $u$ を活性化関数(非線形関数)である $\class{Boldfont}{\textsf{ステップ関数}}$ が変数$XW$をとり、出力 $y$ に $0$ か $1$ を返す。} \\[5pt] \textsf{単純パーセプトロンの機能として、入力がどのような出力を返すか、先ずは $X(x{\tiny 1}{\scriptsize\,+\,\cdots\,+}x{\tiny n})W(w{\tiny 1}{\scriptsize\,+\,\cdots\,+}w{\tiny n}){\hspace{5pt}\small\leqq\hspace{5pt}}0$ } \\ \hspace{10pt}\textsf{の領域と $X\,W{\hspace{5pt}\small\gt\hspace{5pt}}0$ の領域を 直線 $X\,W{\hspace{5pt}\small=\hspace{5pt}}0$ で分離 する ステップ関数の実装から始めるのが機械学習の定番 } \\ \hspace{10pt}\textsf{となる。}\\[5pt] \begin{array}{l}\textsf{ステップ関数} \\ h{\small(x)}{\scriptsize\,=\,}{\scriptsize\left\{\begin{array}{l}1\:(u{\scriptsize\,\geqq\,}0) \\ 0\:(u{\scriptsize\,\lt\,}0)\end{array}\right.}\end{array}\left\{\begin{array}{l}\textsf{単純パーセプトロンに実装される計算処理式は}\hspace{10pt} y{\scriptsize\,=\,}\left\{\begin{array}{l}0\hspace{10pt}w{\tiny 1}x{\tiny 1}{\scriptsize\,+\,\cdots\,+}w{\tiny n}x{\tiny n}{\hspace{5pt}\small\leqq\hspace{5pt}}\theta \\ 1\hspace{10pt}w{\tiny 1}x{\tiny 1}{\scriptsize\,+\,\cdots\,+}w{\tiny n}x{\tiny n}{\hspace{4pt}\gt\hspace{4pt}}\theta\end{array}\right.\hspace{10pt}\textsf{となる。} \\ \\ \textsf{学習では しきい値 $\theta$ に $\boldsymbol b$(バイアス) $\!{\scriptsize\,=\,}1$ を導入するため、上記の数式を式変形する必要がある。} \\ \hspace{30pt}\textsf{$\theta$ を移行して、${\small -}\theta{\scriptsize\,=\,}b$ とすると}\hspace{10pt} y{\scriptsize\,=\,}\left\{\begin{array}{l}0\hspace{10pt}w{\tiny 1}x{\tiny 1}{\scriptsize\,+\,\cdots\,+}w{\tiny n}x{\tiny n}{\scriptsize\,+\,}b{\hspace{5pt}\small\leqq\hspace{5pt}}0 \\ 1\hspace{10pt}w{\tiny 1}x{\tiny 1}{\scriptsize\,+\,\cdots\,+}w{\tiny n}x{\tiny n}{\scriptsize\,+\,}b{\hspace{4pt}\gt\hspace{4pt}}0\end{array}\right.\hspace{10pt}\textsf{となる。} \\[5pt] \textsf{$w{\tiny 1}x{\tiny 1}{\scriptsize\,+\,\cdots\,+}w{\tiny n}x{\tiny n}{\scriptsize\,+\,}b$ は ${\boldsymbol u}(\textsf{ユニット})の$出力になるので}\hspace{10pt}y{\scriptsize\,=\,}\left\{\begin{array}{l}0\hspace{10pt}u{\scriptsize\,\leqq\,}0 \\ 1\hspace{10pt}u{\scriptsize\,\gt\,}0\end{array}\right.\hspace{10pt}\textsf{となる。}\end{array}\right.\end{array}\right.\)