分類
自生している植物が食用であるか否かの判断は、一般消費者には容易ではない。その一例に ニラと間違えてスイセンを誤食してしまい中毒を起こしてしまった事例も多々報告されている。
ニラとスイセンが混生している場所で採取したニラの束を、それぞれ臭いの有無、葉の形状の違いを検査し、二種に分類してみよう。
採取した束に臭い、葉の形状ともに酷似したスイセンが検出された。上図ではグラフの直線を堺に食用であるニラと非食用のスイセンを分離している。この 人による検査 を機械に検査させようというのが 機械学習であり、その手法の一つである 教師あり学習 である。
教師あり学習では、機械に バイアス、重み、正解の値(ここではニラ) の パラメータ(単純パーセプトロンのページで解説) をデータとして与える。このデータを 教師データ という。
では、教師あり学習の2体系、分類と回帰 の 分類 から話しを進めていこう。
2クラス分類の線形識別関数
図2では、グラフに直線を引いてニラとスイセンを分離した。\(\class{Boldfont}{\textsf{線形識別関数}}\) はこの 直線 がキーワードとなる。

\(\textsf{図$1$から}\left\{\begin{array}{l}\textsf{教師あり学習は人の感覚を数値に変換した教師データ(以降、データと記述する)を機械に与える必要がある。} \\[10pt] \textsf{臭いの有無(臭いの強度をランク付けし、あるレベルに堺$({\scriptsize\,=\,}0)$を設けた数値)に入力値として変数$x{\tiny 1}$ を渡す。} \\[5pt] \textsf{葉の形状の違い(葉の長さと幅の比のある度合いに堺$({\scriptsize\,=\,}0)$を設けた数値)に入力値として変数$x{\tiny 2}$ を渡す。} \\[10pt] \textsf{教師あり学習の分類ではクラスを分類$(\small\textsf{ここではニラとスイセンの$2$クラス})$する堺$({\scriptsize\,=\,}0)$を直線 $(\class{Boldfont}{\textsf{識別境界}})$ とし} \\ ~~{\large f}{\small(X)}{\small\,=\,}w{\tiny 0}{\small\,+\,}w{\tiny 1}x{\tiny 1}{\small\,+\,}w{\tiny 2}x{\tiny 2}\left\{\begin{array}{l}\small\textsf{定数項(バイアス項)$w{\tiny 0}$ は バイアスの重み} \\ \small\textsf{係数 $w{\tiny 1},\:w{\tiny 2}$ は 重み} \\ \small\textsf{変数 $x{\tiny 1},\:x{\tiny 2}$ は 入力値}\end{array}\right\}{\small\,=\,}0\hspace{10pt}\textsf{の線形識別式で表記できる。} \\[10pt] \textsf{識別境界$(f{\scriptsize(X)}{\small\,=\,}\small 0)$ で分割された上部のニラの領域を $C{\tiny 1}$、下部のスイセンの領域を $C{\tiny 2}$ とすると、$\class{Boldfont}{\textsf{識別クラス}}$ は} \\ \hspace{10pt}\left\{\begin{array}{l}{\small C}{\tiny 1}\hspace{5pt}f{\scriptsize(X)}{\color{lightgray}{\small\,=\,}{\small w{\tiny 0}{\small\,+\,}w{\tiny 1}x{\tiny 1}{\small\,+\,}w{\tiny 2}x{\tiny 2}}}{\scriptsize\hspace{5pt}\geqq\:}\small 0 \\ {\small C}{\tiny 2}\hspace{5pt}f{\scriptsize(X)}{\color{lightgray}{\small\,=\,}{\small w{\tiny 0}{\small\,+\,}w{\tiny 1}x{\tiny 1}{\small\,+\,}w{\tiny 2}x{\tiny 2}}}{\scriptsize\hspace{5pt}\lt\:}\small 0\end{array}\right.\hspace{10pt}\textsf{で表記される。}(\scriptsize\textsf{$C$は$Class$の頭文字に過ぎない}) \end{array}\right.\)
線形識別関数の定義式は \({\large f}{\scriptsize(X)}{\scriptsize\,=\,}W^{\scriptsize T}X{\scriptsize\,+\,}w{\tiny 0}\) となる。
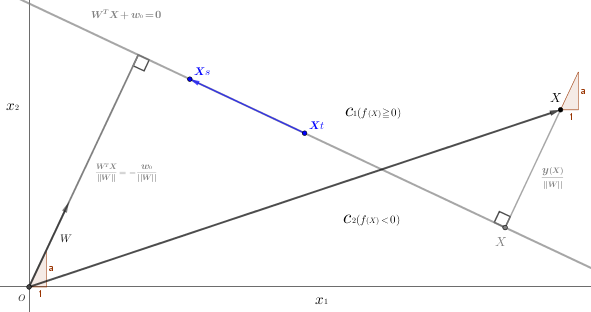
\(\textsf{補足}\left\{\begin{array}{l}\textsf{入力値 $X$ は 次元($\Bbb R$) を表す。図\(1\)では 葉の臭いの有無${\scriptsize\,=\,}{\large x}{\scriptsize 1}$、葉の形状の違い${\scriptsize\,=\,}{\large x}{\scriptsize 2}$ で $2$次元実数空間の記号 で表記する} \\ \hspace{10pt}\textsf{と $\Bbb R^{\scriptsize 2}$ だった。これに、たとえば 葉の色素の濃度${\scriptsize\,=\,}{\large x}{\scriptsize 3}$ 、葉の比重${\scriptsize\,=\,}{\large x}{\scriptsize 4}$、葉の硬さ${\scriptsize\,=\,}{\large x}{\scriptsize 5}\:\cdots\cdots\:$と ${\large x}{\scriptsize d}$ まで入力値} \\ \hspace{10pt}\textsf{を増やし、 $d\,$次元実数空間 $\Bbb R^{\scriptsize d}$ とする。} \\[10pt] \textsf{バイアスを含めた入力値を 入力ベクトル$X{\scriptsize\,=\,}\lbrace {\small 1({\scriptsize\textsf{バイアス}})},x{\tiny 1},x{\tiny 2},x{\tiny 3},\,\cdots\,x{\tiny d}\rbrace$ とすると、} \\ \hspace{10pt}\textsf{それに 係数ベクトル$W{\scriptsize\,=\,}\lbrace w{\tiny 0}({\scriptsize\textsf{バイアス}}),w{\tiny 1},w{\tiny 2},w{\tiny 3},\,\cdots\,w{\tiny d}\rbrace$ が付随して、線形識別関数は $f{\scriptsize (X)}{\scriptsize\,=\,}{\small W^{T}X}{\scriptsize\,+\,}w{\tiny 0}$ とな} \\ \hspace{10pt}\textsf{る。} \\[5pt] \textsf{線形識別関数は ベクトルの内積 で表現されるので、${\small W}{\scriptsize\,=\,}\begin{bmatrix}{\overset{}{\!{\small w}{\tiny 0}\!}} \\[-5pt] \!{\small w}{\tiny 1}\! \\[-5pt] \!{\small w}{\tiny 2}\! \\[-5pt] \!{\small w}{\tiny 3}\! \\[-5pt] \vdots \\[-5pt] \!{\underset{}{{\small w}{\tiny d}}}\! \end{bmatrix},\hspace{5pt}{\small X}{\scriptsize\,=\,}\begin{bmatrix}{\overset{}{\!{\scriptsize 1}\!}} \\[-5pt] \!{\small x}{\tiny 1}\! \\[-5pt] \!{\small x}{\tiny 2}\! \\[-5pt] \!{\small x}{\tiny 3}\! \\[-5pt] \vdots \\[-5pt] \!{\underset{}{{\small x}{\tiny d}}}\! \end{bmatrix}$ の 列ベクトルの積 は 係数ベクトル$\small W$ を } \\ \hspace{10pt}\textsf{転置$({\small W}^{\scriptsize{\class{Boldfont}{T}}})$にして 行ベクトル に変換する。}\hspace{10pt}\Rightarrow\hspace{10pt}\left[ w{\tiny 1},w{\tiny 2},w{\tiny 3},\,\cdots,\,w{\tiny d} \right]\begin{bmatrix}{\overset{}{\!{\small x}{\tiny 1}\!}} \\[-5pt] \!{\small x}{\tiny 2}\! \\[-5pt] \!{\small x}{\tiny 3}\! \\[-5pt] \vdots \\[-5pt] \!{\underset{}{{\small x}{\tiny d}}}\! \end{bmatrix}\hspace{30pt}\large\textsf{☜$\:\href{https://showanojoe.com/template-math/linear-algebra/vector-arithmetic/#2}{\small\textsf{ベクトルの積}}$} \\[5pt] \textsf{図$3$の識別境界の直線$(w{\tiny 0}{\scriptsize\,+\,}w{\tiny 1}x{\tiny 1}{\scriptsize\,+\,}w{\tiny 2}x{\tiny 2}{\scriptsize\,=\,}0)$は、$\Bbb R^{\scriptsize 3}$では $w{\tiny 0}{\scriptsize\,+\,}w{\tiny 1}x{\tiny 1}{\scriptsize\,+\,}w{\tiny 2}x{\tiny 2}{\scriptsize\,+\,}w{\tiny 3}x{\tiny 3}{\scriptsize\,=\,}0$ の 平面、$\Bbb R^{\scriptsize 4}$では $w{\tiny 0}{\scriptsize\,+\,}w{\tiny 1}x{\tiny 1}{\scriptsize\,+\,}w{\tiny 2}$} \\ \hspace{10pt}\textsf{${\scriptsize\,+\,}w{\tiny 3}x{\tiny 3}{\scriptsize\,+\,}w{\tiny 3}x{\tiny 3}{\scriptsize\,=\,}0$ の $?$、$\Bbb R^{\scriptsize 5}$ では $?$、$\Bbb R^{\scriptsize d}$ では $?$。いずれにせよ、$\Bbb R^{\scriptsize 4}$以上の空間は 宇宙か霊の世界 となる} \\ \hspace{10pt}\textsf{ので想像し難いが、すべての空間の識別境界をひっくるめて $\class{Boldfont}{\textsf{超平面}}$ という。超平面 の形状を気にする必要はない。} \\ \hspace{10pt}\textsf{$Python$ が処理してくれる。} \\[10pt] \textsf{原点$o$から識別境界の直線までの距離(線分の長さ)は $\small\displaystyle\frac{w{\tiny 1}x{\tiny 1}{\scriptsize\,+\,}w{\tiny 2}x{\tiny 2}}{\sqrt{w{\tiny 1}^{\tiny 2}{\scriptsize\,+\,}w{\tiny 2}^{\tiny 2}}}{\scriptsize\,-\,}\displaystyle\frac{w{\tiny 0}}{\sqrt{w{\tiny 1}^{\tiny 2}{\scriptsize\,+\,}w{\tiny 2}^{\tiny 2}}}\hspace{10pt}\Rightarrow\hspace{10pt}\scriptsize\displaystyle\frac{\scriptsize{W^{T}X}}{||W||}{\scriptsize\,-\,}\displaystyle\frac{{\small w}{\tiny 0}}{||W||}$} \\[10pt] \hspace{10pt}\left\{\begin{array}{l}\small\textsf{$\scriptsize||\cdot||$ はベクトルの長さ$(\href{https://showanojoe.com/template-math/linear-algebra/scalar-norm/#2}{\textsf{ノルム}})$を表す記号。ここでは $L^{\tiny 2}$ノルム。} \\ \small\textsf{識別境界の直線の式 $w{\tiny 0}{\small\,+\,}w{\tiny 1}x{\tiny 1}{\small\,+\,}w{\tiny 2}x{\tiny 2}{\small\,=\,}0$ を 数学でいう直線の一般形式 $ax{\small\,+\,}by{\small\,+\,}c{\small\,=\,}0$ にあてはめてみると、} \\ \hspace{10pt}\small\textsf{$\href{https://showanojoe.com/template-math/supplementary-material/straight-lines-and-equations/#2}{\textsf{原点から直線までの距離}}$ から理解できる。} \\ \small\textsf{識別境界の式$w{\tiny 0}{\small\,+\,}w{\tiny 1}x{\tiny 1}{\small\,+\,}w{\tiny 2}x{\tiny 2}{\small\,=\,}0$を基本形の式に式変形すると、$x{\tiny 2}{\scriptsize\,=\,}{\scriptsize-}{\scriptsize\displaystyle\frac{w{\tiny 1}}{w{\tiny 2}}}x{\tiny 1}{\scriptsize\,-\,}{\scriptsize\displaystyle\frac{w{\tiny 0}}{w{\tiny 2}}}$。} \\ \hspace{10pt}\small\textsf{$x{\tiny 2}{\scriptsize\,=\,}{\scriptsize\,-\,}{\scriptsize\displaystyle\frac{w{\tiny 1}}{w{\tiny 2}}}x{\tiny 1}{\scriptsize\,-\,}{\scriptsize\displaystyle\frac{w{\tiny 0}}{w{\tiny 2}}}$ から $\href{https://showanojoe.com/template-math/supplementary-material/straight-lines-and-equations/#1}{\textsf{切片}}$ は ${\scriptsize\,-\,}{\scriptsize\displaystyle\frac{w{\tiny 0}}{w{\tiny 2}}}$、入力$x{\tiny 2}$ の重み(係数)は$w{\tiny 2}$ なので バイアスの重み$w{\tiny 0}$ が直線(識別境界)の傾きを決定づ} \\ \hspace{10pt}\small\textsf{けているのがわかる。}\end{array}\right\} \\[10pt] \textsf{図$3$の境界線上の任意の$2$点$p,{\color{gray}p}$は入力$x{\tiny 1},x{\tiny 2}$の出力$y$が$0$($\small\textsf{$x{\tiny 1}$か$x{\tiny 2}$が度合いの堺にあり判別できない}$)の点である。} \\ \hspace{10pt}\textsf{これを$\href{https://showanojoe.com/template-math/linear-algebra/vector-definition/}{\textsf{ベクトル}}\,\overset{\LARGE\vec{\tiny ~}}{{\color{gray}p}p}$ の$\href{https://showanojoe.com/template-math/linear-algebra/position-vector-vector-coordinate-components/}{\textsf{座標成分}}$ $p{\scriptsize\,-\,}{\color{gray}p}$ を識別関数に代入すると、} \\[5pt] \hspace{100pt}{\large f}{\scriptsize(X)}{\scriptsize\,=\,}W^{\scriptsize T}p{\scriptsize\,+\,}w{\tiny 0}{\scriptsize\,-\,}W^{\scriptsize T}{\color{gray}p}{\scriptsize\,+\,}w{\tiny 0}{\scriptsize\,=\,}W^{\scriptsize T}(p{\scriptsize\,-\,}{\color{gray}p}){\scriptsize\,=\,}0 \\[5pt] \hspace{10pt}\textsf{となる。これより $\color{red}\underline{\color{black}\textsf{超平面(ここでの直線)は重み$\left({\small W^{\scriptsize T}}\right)$ に 直交する}}$ といえる。}\end{array}\right.\)

