回帰
教師あり学習(分類と回帰)\(1\) ではニラとスイセンという 離散的な対象(オブジェクト)を\(2\)クラス分類 した。
回帰では、連続した数値を予測 する。
単回帰分析
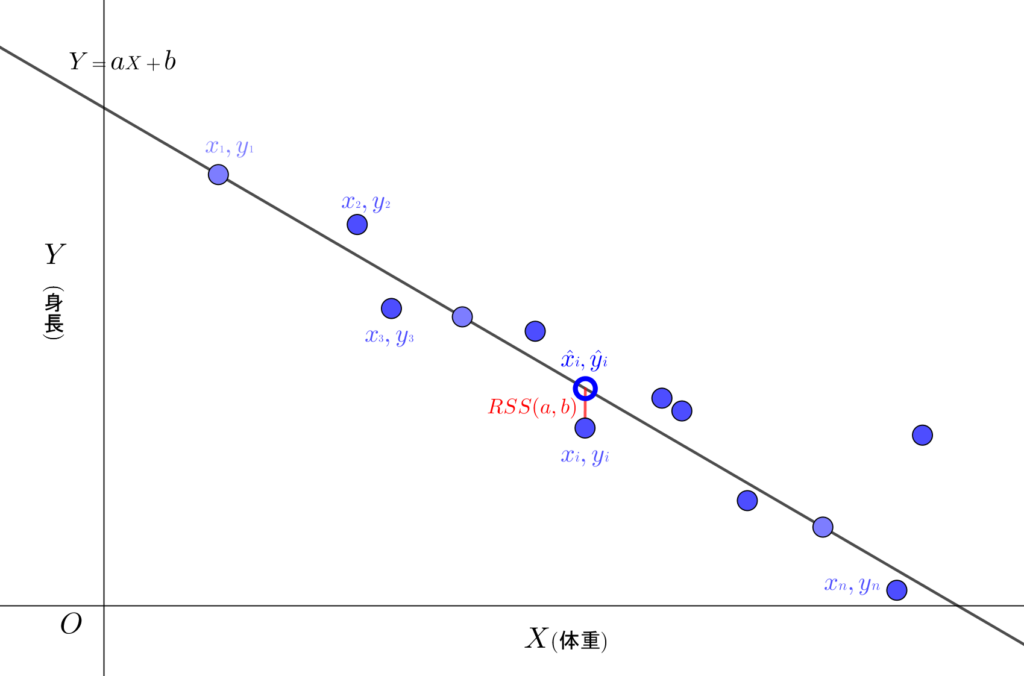
\(\textsf{図\(1\)から}\left\{\begin{array}{l}\textsf{単回帰分析(以降、単回帰と記述)とは、$(x{\tiny 1},y{\tiny 1}),(x{\tiny 2},y{\tiny 2}),(x{\tiny 3},y{\tiny 3}),\cdots,(x{\tiny i},y{\tiny i}),\cdots,(x{\tiny n},y{\tiny n})$ のそれぞれの実測値} \\ \hspace{10pt}\textsf{(これを$D$と置く)の近似値をとる直線(線形)を設定し、そこから予測値を得る手法(アルゴリズム)をいう。}\\[10pt] \textsf{例として、体重と身長の割合を$D$とし、体重$X$から身長$Y$を予測する解析なら$X$が説明変数、$Y$が目的変数になる。} \\[10pt]\textsf{$D$の近似値をとる線形関数は $Y{\scriptsize\,=\,}a{\small X}{\scriptsize\,+\,}b$ である。単回帰は $Y{\scriptsize\,=\,}a{\small X}{\scriptsize\,+\,}b$ から $a,b(\textsf{回帰係数})$ を求めることが課題と} \\ \hspace{10pt}\textsf{なる。 } \\[10pt] \textsf{$D$の任意のデータ$(x{\tiny i},y{\tiny i})$ と、そこから得た予測値$(\hat{x{\tiny i}},\hat{y{\tiny i}})$との ズレ は赤い線分の長さ $\color{red}\small{RSS(a,b)}$ で $\class{Boldfont}{\textsf{残差平方和}}$} \\ \hspace{10pt} \textsf{といい、 $\small{RSS(a,b)}{\scriptsize\,=\,}\displaystyle\sum_{i=1}^n \left\{y{\tiny i}{\scriptsize\,-\,}(ax{\tiny i}{\scriptsize\,+\,}b)\right\}^2$ の計算$(\class{Boldfont}{\textsf{最小二乗法}})$で導出できる。}\end{array}\right.\)

