$$\begin{array}{l}\textsf{ベクトルの内積 とは、$1$行$n$列}({\small\textsf{ベクトル $\class{Boldfont}{b}$ を行列と解釈するのなら、}\class{Boldfont}{b}={\tiny\begin{bmatrix}\overset{}{b_x} \\ b_y\end{bmatrix}} \textsf{ の$1$行$2$列の行列である。}}) \textsf{の射影行列とベクトル$(\small\class{Boldfont}{a})$の積であり、} \\[5pt] \textsf{$2$次元や$3$次元の行列(複合ベクトル=行列)を $1$ 次元化$({\small\textsf{射影}})$することである。} \end{array}$$
$$\class{Boldfont}{\textsf{ベクトルの内積の定義式}}\hspace{10pt}|\class{Boldfont}{a}|\cdot|\class{Boldfont}{b}|cos{\theta}$$
$$\textsf{ベクトルの内積は $\class{Boldfont}{a}$ に射影された $\class{Boldfont}{b}$ の線分 $\overline{\large{{\color{red}{o}}{\color{blue}{p}}}}$ の値$(\small\textsf{長さ})$と $\class{Boldfont}{a}$ のスカラー値の積で求まる。}$$
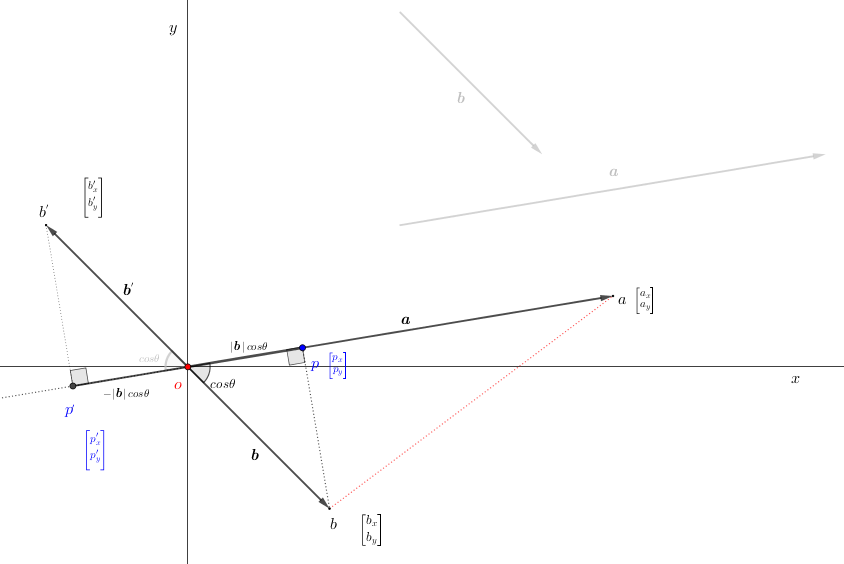
$$\textsf{図$1$から}\left\{\begin{array}{l} \textsf{絶対値記号 $(\class{Boldfont}{{\scriptsize{|\,|}}})$ で囲った$|\class{Boldfont}{a}|\,$は$\,\boldsymbol a\,$の大きさ($\small\textsf{スカラー値}$)を表す。$~\,|\class{Boldfont}{b}|\,$も同様。 } \\[5pt] |\class{Boldfont}{a}|\cdot|\class{Boldfont}{b}|cos{\theta}{\,=\,|\class{Boldfont}{a}|\,\cdot\,\overline{{\color{red}{o}}{\color{blue}{p}}}({\small{=|\class{Boldfont}{b}|\,cos\theta}})} \hspace{50pt} \left\{ \scriptsize{cos\theta}=\scriptsize\displaystyle\frac{\overline{{\color{red}{o}}{\color{blue}{p}}}}{|\class{Boldfont}{b}|} \right\} \\[5pt] \overline{{\color{red}{o}}{\color{blue}p}}\,=\,|b|\,cos\theta\,\textsf{ は $\small\color{lightgray}{\textsf{雛形数学 > 三角関数 > }}$ $\href{https://showanojoe.com/template-math/trigonometric-function/cosine-trigonometric-ratio/}{\small\textsf{余弦($cos\,\theta$),$\,$正弦($sin\,\theta$),$\,$正接($tan\,\theta$)の三角比}}$ を参照。} \\[5pt] \textsf{$ \hspace{5pt}\,|\class{Boldfont}{b}|\,cos\theta\, $は実数値(線分 $\,\overline{{\color{red}{o}}{p}}\,$の大きさ(長さ))となるので、 内積の定義式$\,|{\boldsymbol a}|\cdot|{\boldsymbol b}|cos\large\theta$}\\ \textsf{は $\,|{\boldsymbol a}| \,$の 実数倍($\,|{\boldsymbol a}|\leq|{\boldsymbol b}|\,$なら $\,|{\boldsymbol b}|\,$の 実数倍 ) となる。 } \hspace{50pt}\left\{\,\small{|\class{Boldfont}{a}|\cdot|\class{Boldfont}{b}|cos{\theta}=|\class{Boldfont}{b}|\cdot|\class{Boldfont}{a}|cos{\theta}\:\textsf{で可換(交換法則が成り立つ)である。}}\,\right\} \\[5pt] \textsf{射影が$-|\class{Boldfont}{b}|cod\theta$の場合、その内積は “負” の値となる。}\hspace{50pt}\{\textsf{$\small\color{lightgray}{\textsf{雛形数学 > 三角関数 > }}$ $\href{https://showanojoe.com/template-math/trigonometric-function/cosine-trigonometric-ratio/}{\small\textsf{余弦($cos\,\theta$),$\,$正弦($sin\,\theta$),$\,$正接($tan\,\theta$)の三角比}}$ を参照。}\} \\[5pt] \cssId{1-1}{\textsf{射影が点になる、すなわち 内積が$0$ なら $\boldsymbol a$ と $b$ は直交しているといえる。}}\end{array}\right. $$
$$\begin{array}{l} \textsf{内積の定義式$|\class{Boldfont}{a}|\cdot|\class{Boldfont}{b}|cos{\theta}=$} \\[5pt] \textsf{${\boldsymbol a},\,{\boldsymbol b}\,$の $\class{Boldfont}{\textsf{座標成分による内積の公式}}$$\,x_{\small1}x_{\small2}\,{\small+}\,y_{\small1}y_{\small2}$} \end{array} \left\{\begin{array}{l}\textsf{証明$\;\Rightarrow\;\hspace{5pt}|\class{Boldfont}{a}|\,=\,\sqrt{\mathstrut{{x_{\small1}}^{\small2}\,{\small+}\,{y_{\small1}}^{\small2}}},\hspace{10pt} |{\boldsymbol b}|\,=\, \sqrt{\mathstrut{{x_{\small2}}^{\small2}\,{\small+}\,{y_{\small2}}^{\small2}}} $}\\[5pt] \hspace{26pt}\hookrightarrow\hspace{10pt}\textsf{$\LARGE\overline{\normalsize ba}$ $\small\textsf{(赤い点線分)}$の長さ$\,=\,(x_{\small1}-x_{\small2},\,y_{\small1}-y_{\small2})$}\\[5pt] \hspace{26pt}\hookrightarrow\hspace{10pt}\left\{\small\textsf{}\right\}|{\LARGE\overrightarrow{\normalsize ba}}|\,=\, \sqrt{\mathstrut{({x_{\small1}}\,{\small-}\,{x_{\small2}})^{\small2}\,{\small+}\,({y_{\small1}} \,{\small-}\,{y_{\small2}})^{\small2}}}\\[5pt] \hspace{26pt}\hookrightarrow\hspace{10pt} \sqrt{\mathstrut{|\LARGE\overrightarrow{\normalsize ba}}}|^{\small2}=\sqrt{\mathstrut{{|\boldsymbol a}|^{\small2}+|{\boldsymbol b}|^{\small2}\,{\small-}\,2|{\boldsymbol a}||{\boldsymbol b}|\,cos\theta}}\hspace{15pt}\left\{{\color{lightgray}{\small\textsf{雛形数学 > 三角関数 > }}}{\href{https://showanojoe.com/template-math/trigonometric-function/cosine-theorem/}{\small\textsf{余弦定理}}} \small\textsf{を参照。}\hspace{-10pt} \right\}\\[5pt] \hspace{26pt}=\hspace{10pt} \boldsymbol{cos\theta}\,=\,\scriptsize{\displaystyle{\frac{\sqrt{\mathstrut{|{\boldsymbol a}|^{\small2}{\small+}|{\boldsymbol b}|^{\small2}{\small-}|{\LARGE\vec{\normalsize ba}}|^{\small2}}}}{\sqrt{\mathstrut{2|{\boldsymbol a}||{\boldsymbol b}|}}}}}\hspace{15pt}\left\{\begin{array}{l}\small{\textsf{上記の余弦定理の公式を式変形。}}\\ \small{\textsf{以下、成分を代入して証明計算。}}\end{array}\right\}\\[5pt] \hspace{26pt}=\hspace{10pt}\displaystyle{\frac{(\sqrt{\mathstrut{{x_1}^{\small2}{\small+}{y_1}^{\small2}}})^2{\small+}(\sqrt{\mathstrut{{x_2}^{\small2}{\small+}{x_2}^{\small2}}})^2{\small-} (\sqrt{\mathstrut{({x_{\small1}}\,{\small-}\,{x_{\small2}})^{\small2}\,{\small+}\,({y_{\small1}} \,{\small-}\,{y_{\small2}})^{\small2}}})^2}{2 \sqrt{\mathstrut{{x_{\small1}}^{\small2}\,{\small+}\,{y_{\small1}}^{\small2}}} \sqrt{\mathstrut{{x_{\small2}}^{\small2}\,{\small+}\,{y_{\small2}}^{\small2}}}}}\\[5pt] \hspace{26pt}=\hspace{10pt}\displaystyle{\frac{{x_{\small1}}^{\small2}{\small+}{x_{\small2}}^{\small2}{\small+}{y_{\small1}}^{\small2}{\small+}{y_{\small2}}^{\small2}{\small-}({x_{\small1}}^{\small2}{\small-}2{x_{\small1}}{x_{\small2}}{\small+}{x_{\small2}}^{\small2}{\small+}{y_{\small1}}^{\small2}{\small-}2{y_{\small1}}{y_{\small2}}{\small+}{y_{\small2}}^{\small2} )}{ 2 \sqrt{\mathstrut{{x_{\small1}}^{\small2}\,{\small+}\,{y_{\small1}}^{\small2}}} \sqrt{\mathstrut{{x_{\small2}}^{\small2}\,{\small+}\,{y_{\small2}}^{\small2}}}}}\\[5pt] \hspace{26pt}=\hspace{10pt}\displaystyle{\frac{2{x_{\small1}}{x_{\small2}}{\small+} 2{y_{\small1}}{y_{\small2}} }{ 2 \sqrt{\mathstrut{{x_{\small1}}^{\small2}\,{\small+}\,{y_{\small1}}^{\small2}}} \sqrt{\mathstrut{{x_{\small2}}^{\small2}\,{\small+}\,{y_{\small2}}^{\small2}}}}}\\[5pt] \hspace{26pt}=\hspace{10pt}\displaystyle{\frac{{x_{\small1}}{x_{\small2}}{\small+}{y_{\small1}}{y_{\small2}} }{\sqrt{\mathstrut{{x_{\small1}}^{\small2}\,{\small+}\,{y_{\small1}}^{\small2}}} \sqrt{\mathstrut{{x_{\small2}}^{\small2}\,{\small+}\,{y_{\small2}}^{\small2}}}}}\\[5pt] \hspace{26pt}\hookrightarrow\hspace{10pt}{\boldsymbol a}\cdot{\boldsymbol b}= |{\boldsymbol a}||{\boldsymbol b}|\,cos\,{\large\theta} \;\Rightarrow\; \sqrt{\mathstrut{{x_{\small1}}^{\small2}\,{\small+}\,{y_{\small1}}^{\small2}}} \sqrt{\mathstrut{{x_{\small2}}^{\small2}\,{\small+}\,{y_{\small2}}^{\small2}}}\;\displaystyle{\frac{{x_{\small1}}{x_{\small2}}{\small+}{y_{\small1}}{y_{\small2}} }{\sqrt{\mathstrut{{x_{\small1}}^{\small2}\,{\small+}\,{y_{\small1}}^{\small2}}} \sqrt{\mathstrut{{x_{\small2}}^{\small2}\,{\small+}\,{y_{\small2}}^{\small2}}}}}\\[5pt] \hspace{26pt}=\hspace{10pt} x_{\small1}x_{\small2}\,{\small+}\,y_{\small1}y_{\small2} \end{array}\right. $$
\(\textsf{ベクトル $\overset{\large\vec{\tiny ~}}{a},\vec{b}$ において、その内積が$0$}\left\{\begin{array}{l}\textsf{$|{\boldsymbol b}|cos\theta{\scriptsize\,=\,}0$} \\[5pt] \textsf{$cos\theta{\scriptsize\,=\,}0{\scriptsize\,=\,}90^{\circ}$}\end{array}\right\}\hspace{5pt}\textsf{の場合、$\overset{\large\vec{\tiny ~}}{a}$ と $\vec{b}$ は 直交 している。}\)
直交射影について
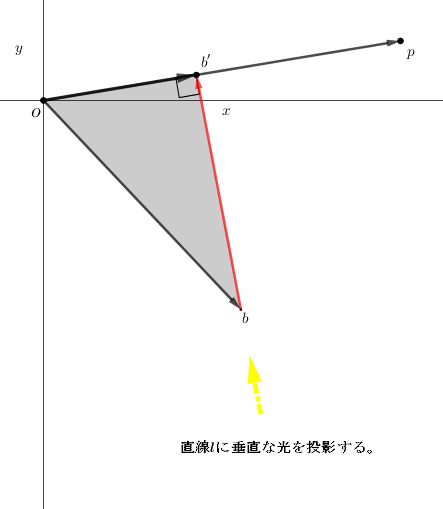
\(\textsf{図$2$から}\left\{\begin{array}{l}\textsf{直交射影は、$\Large\vec{\normalsize ob^{\prime}}$ を求めることが課題となる。} \\ \textsf{ベクトル$\overset {\LARGE\vec{\tiny ~}}{op}$ に垂直な光を投影し、$\Large\vec{\normalsize ob}$ が成す影の堺を 点$b^{\prime}$ とする。} \\ \textsf{ベクトル$\overset {\LARGE\vec{\tiny ~}}{op}$上に $\Large\vec{\normalsize ob^{\prime}}$ を置くと $\Large\vec{\normalsize ob}{\small\perp}\Large\vec{\normalsize bb^{\prime}}$($\small\perp$は垂直を意味する記号)となる。} \\ \textsf{では直交射影$\Large\vec{\normalsize ob^{\prime}}$を導出する。}\left\{\begin{array}{l}{\Large\vec{\normalsize ob}}\cdot\overset{\LARGE\vec{\tiny ~}}{op}{\scriptsize\,=\,}|{\Large\vec{\normalsize ob}}|\times|{\Large\vec{\normalsize ob^{\prime}}}|\hspace{10pt}\left\{\small\textsf{図$1$ と 図$1$から を参照}\right\} \\ {\scriptsize\,\hookrightarrow\:}|{\Large\vec{\normalsize ob^{\prime}}}|{\scriptsize\,=\,}\scriptsize\displaystyle\frac{{\large\vec{\scriptsize ob}}\cdot\overset{\LARGE\vec{\tiny ~}}{op}}{|{\large\vec{\scriptsize ob}}|} \\ {\scriptsize\,\hookrightarrow\:}{\Large\vec{\normalsize ob^{\prime}}}{\scriptsize\,=\,}|{\Large\vec{\normalsize ob^{\prime}}}|\times\scriptsize\displaystyle\frac{{\large\vec{\scriptsize ob}}}{|{\large\vec{\scriptsize ob}}|}{\scriptsize\,=\,}\scriptsize\displaystyle\frac{{\large\vec{\scriptsize ob}}\cdot\overset{\LARGE\vec{\tiny ~}}{op}}{|{\large\vec{\scriptsize ob}}|}\times\scriptsize\displaystyle\frac{{\large\vec{\scriptsize ob}}}{|{\large\vec{\scriptsize ob}}|}{\scriptsize\,=\,}\scriptsize\displaystyle\frac{{\large\vec{\scriptsize ob}}\cdot\overset{\LARGE\vec{\tiny ~}}{op}}{{\normalsize(}|{\large\vec{\scriptsize ob}}|{\normalsize)}^{\!2}}{\large\vec{\scriptsize ob}} \\ {\scriptsize\,\hookrightarrow\:}\Large\vec{\normalsize ob^{\prime}}{\scriptsize\,=\,}\scriptsize\displaystyle\frac{{\large\vec{\scriptsize ob}}\cdot\overset{\LARGE\vec{\tiny ~}}{op}}{{\normalsize(}|{\large\vec{\scriptsize ob}}|{\normalsize)}^{\!2}}{\large\vec{\scriptsize ob}}\end{array}\right\}\end{array}\right.\)
