位置ベクトルについて
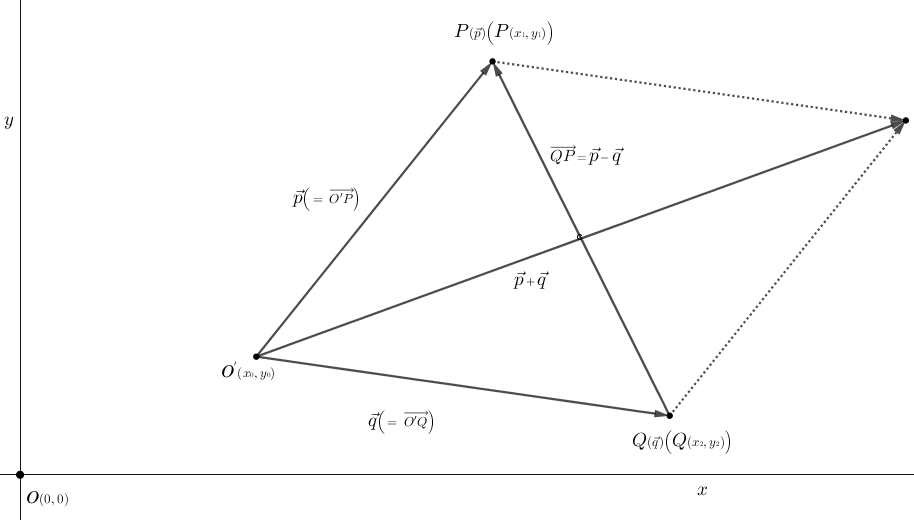
\(\textsf{図$1$から}\left\{\begin{array}{l}\textsf{平面上(空間内)のそれぞれのベクトルの始点を一つの基準点に置く。ここでは基準点を$O^{\small\prime}$としたが、} \\ \hspace{10pt}\textsf{$\color {red}{\underline{\color{black}\textsf{ベクトルの基準点は課題により適材適所に置かれる}}}$。} \\[10pt] \textsf{${\color{lightgray}O^{\small\prime}\:\textsf{を基準点とした}}$ $\vec{p}$ は 点$P$ の位置ベクトルである。${\color{lightgray}O^{\small\prime}\:\textsf{を基準点とした}}$ $\vec{q}$ は 点$Q$ の位置ベクトルである。} \\[10pt] \textsf{位置ベクトルは基準点の位置に関わらず、一律に}\:\left\{\begin{array}{l}\small\textsf{$\normalsize\vec{p}$ は 点$\normalsize P$ の位置ベクトルである と提示した場合、点$\normalsize P$ は ${\normalsize P}({\small\vec{p}})$ と表記される} \\ \small\textsf{$\normalsize\vec{q}$ は 点$\normalsize Q$ の位置ベクトルである と提示した場合、点$\normalsize Q$ は ${\normalsize Q}({\small\vec{q}})$ と表記される}\end{array}\right\} \:\textsf{ことが多い。} \end{array}\right.\)
ベクトルの座標成分について
\(\textsf{図$1$から}\left\{\begin{array}{l}\textsf{$\overset{\Large\vec{\tiny ~}}{p}$ の座標成分は $\overset{\Huge\vec{\tiny ~}}{\small O^{\small\prime}P}$ より、$(x{\tiny 1}{\scriptsize\,-\,}x{\tiny 0},\:y{\tiny 1}{\scriptsize\,-\,}y{\tiny 0})$ で $\small\begin{bmatrix}x{\tiny 1}{\scriptsize\,-\,}x{\tiny 0} \\ y{\tiny 1}{\scriptsize\,-\,}y{\tiny 0}\end{bmatrix}$。}\hspace{30pt}\left\{\begin{array}{l}\small\textsf{ベクトルの座標成分は 終点${\scriptsize\,-\,}$始点(ここでは$P{\scriptsize \,- \,}O^{\small\prime}$)である。成分表示は 縦ベクトル($[\:\:]$または$(\:)$内に} \\ \small\textsf{成分を縦に配列する。ただそれだけのこと。) で表記する。} \end{array}\right\} \\ \textsf{$\overset{\Large\vec{\tiny ~}}{q}$ の座標成分は $\overset{\Huge\vec{\tiny ~}}{\small O^{\small\prime}Q}$ より、$(x{\tiny 2}{\scriptsize\,-\,}x{\tiny 0},\:y{\tiny 2}{\scriptsize\,-\,}y{\tiny 0})$ で $\small\begin{bmatrix}x{\tiny 2}{\scriptsize\,-\,}x{\tiny 0} \\ y{\tiny 2}{\scriptsize\,-\,}y{\tiny 0}\end{bmatrix}$。}\end{array}\right.\)
図\(1\)の補足
\(\vec{p}{\scriptsize\,+\,}\vec{q}\) は 点\(O^{\prime}\) を始点とするベクトル \(\vec{a}\) の終点と、平行移動させたベクトル \(\vec{q}\) の始点が同じ点を経由しその終点に至るベクトルである。これは ベクトルの和 である。ベクトルの差 はベクトルの和とは逆の見方で \(\Huge\vec{\small QP}\) を \(\overset{\Large\vec{\tiny ~}}{p}\) と \(\overset{\Large\vec{\tiny ~}}{q}\) に 分解する 形となる。\(\Huge\vec{\small QP}\) は 点\(Q\) から 点\(O^{\prime}\) を経由して 点\(P\) に至るベクトルとなるので \(\overset{\Large\vec{\tiny ~}}{q}\) は 逆ベクトル \({\scriptsize\,-\,}\overset{\Large\vec{\tiny ~}}{q}\) となり、\({\Huge\vec{\small QP}}{\scriptsize\,=\,}\overset{\Large\vec{\tiny ~}}{p}{\scriptsize\,-\,}\overset{\Large\vec{\tiny ~}}{q}\) となる。
