円の方程式

円の方程式の単元は、課題とする円の$\color{red}\underline{\color{black}\textsf{円周上の任意の点$(x,\,y)$と中心点、半径$({\color{red}\large r})$との関係}}$を方程式$(\textsf{等式})$で表す学習となる。

円の方程式$({\textsf{基本形}})$

$\hspace{5pt}(x{\small\,-\,}a)^{2}+(y{\small\,-\,}b)^{2}{\small\,=\,}r^{2}$

円の方程式$({\textsf{一般形}})$

$\hspace{5pt}x^{2}{\small\,+\,}y^{2}{\small\,+\,}Ax{\small\,+\,}By{\small\,+\,}C{\small\,=\,}0$

$(x{\small\,-\,}a)^{2}+(y{\small\,-\,}b)^{2}{\small\,=\,}r^{2}$$\hspace{10pt}{\small\Rightarrow}\hspace{10pt}$$x^{2}{\small\,-\,}2ax{\small\,+\,}a^{2}{\small\,+\,}y^{2}{\small\,-\,}2bx{\small\,+\,}b^{2}{\small\,-\,}r^{2}{\small\,=\,}0$$\hspace{10pt}{\small\Rightarrow}\hspace{10pt} x^{2}{\small\,+\,}y^{2}{\small\,+\,}({\small\,-\,}2a)x{\small\,+\,}({\small\,-\,}2b)y{\small\,+\,}a^{2}{\small\,+\,}b^{2}{\small\,-\,}r^{2}{\small\,=\,}0$
${\small\,-\,}2a$ を $A$、${\small\,-\,}2b$ を $B$、$a^{2}{\small\,+\,}b^{2}{\small\,-\,}r^{2}{\small\,=\,}0$ を $C$ と置くと一般形の円の方程式になる。

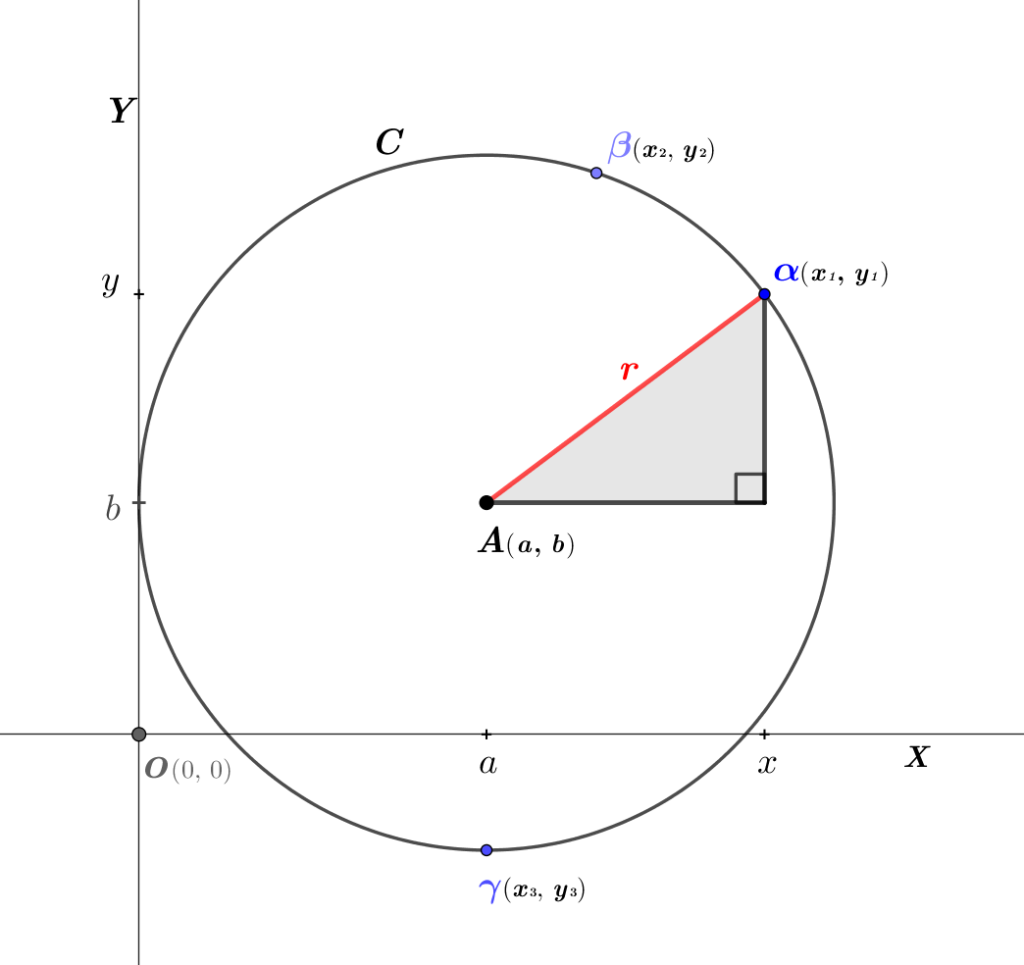
円の方程式の基本形は $\href{https://showanojoe.com/template-math/trigonometric-function/three-squares-theorem/}{\textsf{三平方の定理}}$ で考えると理解しやすい。
図$1$の円$C$の半径は ${\color{red}\large r}(\textsf{変数})$ である。
一般形の円の方程式は基本形を$\href{https://showanojoe.com/template-math/supplementary-material/factor/#因数とは}{\textsf{展開}}$整理した円の方程式になる。逆に、一般形の円の方程式を平方完成した式が基本形の円の方程式になり、中心点の座標と半径が見いだされる。
図$1$の円周上を通る複数の任意の点$(\textsf{$\alpha$および$\beta,\,\gamma$})$と中心点$A$と半径${\color{red}\large r}$との関係は円の方程式の一般形を用いて解決する。