\(\textsf{平面の方程式}\hspace{10pt}ax{\scriptsize\,+\,}by{\scriptsize\,+\,}cz{\scriptsize\,+\,}d{\scriptsize\,=\,}0\)
\(3\)つの定点よる平面の方程式

\(\textsf{図$1$から}\left\{\begin{array}{l}\textsf{平面の式は平面上の$3$定点で求まる。} \\[10pt] \textsf{$3$つの定点$A,B,C$に平面が通る。定点の座標成分をそれぞれ $(a{\tiny x},a{\tiny y},a{\tiny z}),(b{\tiny x},b{\tiny y},b{\tiny z}),(c{\tiny x},c{\tiny y},c{\tiny z})$ とする。} \\[10pt] \textsf{この$3$点$A,B,C$を通る平面上に任意の点$\color{red}p(x,y,z)$ を置く。} \\[10pt] {\huge\vec{\small A{\color{red}p}}}{\scriptsize\,=\,}s\,{\huge\vec{\small AB}}{\scriptsize\,+\,}t\,{\huge\vec{\small AC}}\,\textsf{が成り立ち、これを座標成分の式にすると、} \\[5pt]\hspace{10pt}\left\{\begin{array}{l}\small\left\{{\color{red}(x,y,z)}{\scriptsize\,-\,}(a{\tiny x},a{\tiny y},a{\tiny z})\right\}{\scriptsize\,=\,}s\left\{(b{\tiny x},b{\tiny y},b{\tiny z}){\scriptsize\,-\,}(a{\tiny x},a{\tiny y},a{\tiny z})\right\}{\scriptsize\,+\,}t\left\{(c{\tiny x},c{\tiny y},c{\tiny z}){\scriptsize\,-\,}(a{\tiny x},a{\tiny y},a{\tiny z})\right\}\hspace{5pt}\{\small\textsf{$s,t$は$\href{https://showanojoe.com/template-math/supplementary-material/straight-lines-and-equations/#3}{\textsf{媒介変数}}$、$s{\scriptsize\,+\,}t{\scriptsize\,=\,}1$の性質をもつ。}\} \\ \hookrightarrow\small{\left\{(x{\scriptsize\,-\,}a{\tiny x}\:\:y{\scriptsize\,-\,}a{\tiny y}\:\:z{\scriptsize\,-\,}a{\tiny z})\right\}{\scriptsize\,=\,}\left\{s(b{\tiny x}{\scriptsize\,-\,}a{\tiny x}){\scriptsize\,+\,}t(c{\tiny x}{\scriptsize\,-\,}a{\tiny x})\:\:s(b{\tiny y}{\scriptsize\,-\,}a{\tiny y}){\scriptsize\,+\,}t(c{\tiny y}{\scriptsize\,-\,}a{\tiny y})\:\:s(b{\tiny z}{\scriptsize\,-\,}a{\tiny z}){\scriptsize\,+\,}t(c{\tiny z}{\scriptsize\,-\,}a{\tiny z})\right\}} \\ \hookrightarrow\hspace{15pt}\left.\begin{array}{l}\small{x{\scriptsize\,-\,}a{\tiny x}{\scriptsize\,=\,}s(b{\tiny x}{\scriptsize\,-\,}a{\tiny x}){\scriptsize\,+\,}t(c{\tiny x}{\scriptsize\,-\,}a{\tiny x})} \\ \small{y{\scriptsize\,-\,}a{\tiny y}{\scriptsize\,=\,}s(b{\tiny y}{\scriptsize\,-\,}a{\tiny y}){\scriptsize\,+\,}t(c{\tiny y}{\scriptsize\,-\,}a{\tiny y})} \\ \small{z{\scriptsize\,-\,}a{\tiny z}{\scriptsize\,=\,}s(b{\tiny z}{\scriptsize\,-\,}a{\tiny z}){\scriptsize\,+\,}t(c{\tiny z}{\scriptsize\,-\,}a{\tiny z})}\end{array}\right\}\small\textsf{これらの座標成分の式から媒介変数$s,t$を消去する。} \\ \end{array}\right\} \\ \hookrightarrow\hspace{10pt}\left\{\begin{array}{l}\small{s{\scriptsize\,=\,}\displaystyle\frac{x{\scriptsize\,-\,}a{\tiny x}{\scriptsize\,-\,}t(c{\tiny x}{\scriptsize\,-\,}a{\tiny x})}{b{\tiny x}{\scriptsize\,-\,}a{\tiny x}}{\scriptsize\,=\,}\displaystyle\frac{y{\scriptsize\,-\,}a{\tiny y}{\scriptsize\,-\,}t(c{\tiny y}{\scriptsize\,-\,}a{\tiny y})}{b{\tiny y}{\scriptsize\,-\,}a{\tiny y}}{\scriptsize\,=\,}\displaystyle\frac{z{\scriptsize\,-\,}a{\tiny z}{\scriptsize\,-\,}t(c{\tiny z}{\scriptsize\,-\,}a{\tiny z})}{b{\tiny z}{\scriptsize\,-\,}a{\tiny z}}}\hspace{10pt}\textsf{これを 通分 する。} \\ \hookrightarrow\small{(b{\tiny y}{\scriptsize\,-\,}a{\tiny y})(b{\tiny z}{\scriptsize\,-\,}a{\tiny z})\{{x{\scriptsize\,-\,}a{\tiny x}{\scriptsize\,-\,}tc{\tiny x}{\scriptsize\,+\,}ta{\tiny x}}\}{\scriptsize\,=\,}(b{\tiny y}{\scriptsize\,-\,}a{\tiny y})(b{\tiny z}{\scriptsize\,-\,}a{\tiny z})\{{y{\scriptsize\,-\,}a{\tiny y}{\scriptsize\,-\,}tc{\tiny y}{\scriptsize\,+\,}ta{\tiny y}}\}{\scriptsize\,=\,}(b{\tiny x}{\scriptsize\,-\,}a{\tiny x})(b{\tiny y}{\scriptsize\,-\,}a{\tiny y})\{{z{\scriptsize\,-\,}a{\tiny z}{\scriptsize\,-\,}tc{\tiny z}{\scriptsize\,+\,}ta{\tiny z}}\}} \\ \hookrightarrow\small{\{b{\tiny y}b{\tiny z}{\scriptsize\,-\,}b{\tiny y}a{\tiny z}{\scriptsize\,-\,}a{\tiny y}b{\tiny z}{\scriptsize\,+\,}a{\tiny y}a{\tiny z}\}\{{x{\scriptsize\,-\,}a{\tiny x}{\scriptsize\,-\,}tc{\tiny x}{\scriptsize\,+\,}ta{\tiny x}}\}{\scriptsize\,=\,}\{b{\tiny x}b{\tiny z}{\scriptsize\,-\,}b{\tiny x}a{\tiny z}{\scriptsize\,-\,}a{\tiny x}b{\tiny z}{\scriptsize\,+\,}a{\tiny x}a{\tiny z}\}\{{y{\scriptsize\,-\,}a{\tiny y}{\scriptsize\,-\,}tc{\tiny y}{\scriptsize\,+\,}ta{\tiny y}}\}{\scriptsize\,=\,}\{b{\tiny x}b{\tiny y}{\scriptsize\,-\,}b{\tiny x}a{\tiny y}{\scriptsize\,-\,}a{\tiny x}b{\tiny y}{\scriptsize\,+\,}a{\tiny x}a{\tiny y}\}\{{z{\scriptsize\,-\,}a{\tiny z}{\scriptsize\,-\,}tc{\tiny z}{\scriptsize\,+\,}ta{\tiny z}}\}} \\ \hookrightarrow\small{{b{\tiny y}b{\tiny z}x{\scriptsize\,-\,}b{\tiny y}b{\tiny z}a{\tiny x}{\scriptsize\,-\,}b{\tiny y}b{\tiny z}tc{\tiny x}{\scriptsize\,+\,}b{\tiny y}b{\tiny z}ta{\tiny x}}{{\scriptsize\,-\,}b{\tiny y}a{\tiny z}x{\scriptsize\,+\,}b{\tiny y}a{\tiny z}a{\tiny x}{\scriptsize\,+\,}b{\tiny y}a{\tiny z}tc{\tiny x}{\scriptsize\,-\,}b{\tiny y}a{\tiny z}ta{\tiny x}}{{\scriptsize\,-\,}a{\tiny y}b{\tiny z}x{\scriptsize\,+\,}a{\tiny y}b{\tiny z}a{\tiny x}{\scriptsize\,+\,}a{\tiny y}b{\tiny z}tc{\tiny x}{\scriptsize\,-\,}a{\tiny y}b{\tiny z}ta{\tiny x}}{\scriptsize\,+\,}{a{\tiny y}a{\tiny z}x{\scriptsize\,-\,}a{\tiny y}a{\tiny z}a{\tiny x}{\scriptsize\,-\,}a{\tiny y}a{\tiny z}tc{\tiny x}{\scriptsize\,+\,}a{\tiny y}a{\tiny z}ta{\tiny x}}} \\ \small{{\scriptsize\,=\,}{b{\tiny x}b{\tiny z}y{\scriptsize\,-\,}b{\tiny x}b{\tiny z}a{\tiny y}{\scriptsize\,-\,}b{\tiny x}b{\tiny z}tc{\tiny y}{\scriptsize\,+\,}b{\tiny x}b{\tiny z}ta{\tiny y}}{{\scriptsize\,-\,}b{\tiny x}a{\tiny z}y{\scriptsize\,+\,}b{\tiny x}a{\tiny z}a{\tiny y}{\scriptsize\,+\,}b{\tiny x}a{\tiny z}tc{\tiny y}{\scriptsize\,-\,}b{\tiny x}a{\tiny z}ta{\tiny y}}{{\scriptsize\,-\,}a{\tiny y}b{\tiny z}y{\scriptsize\,+\,}a{\tiny x}b{\tiny z}a{\tiny y}{\scriptsize\,+\,}a{\tiny y}b{\tiny z}tc{\tiny y}{\scriptsize\,-\,}a{\tiny x}b{\tiny z}ta{\tiny y}}{\scriptsize\,+\,}{a{\tiny x}a{\tiny z}y{\scriptsize\,-\,}a{\tiny x}a{\tiny z}a{\tiny y}{\scriptsize\,-\,}a{\tiny x}a{\tiny z}tc{\tiny y}{\scriptsize\,+\,}a{\tiny x}a{\tiny z}ta{\tiny y}}} \\ \small{{\scriptsize\,=\,}{b{\tiny x}b{\tiny z}z{\scriptsize\,-\,}b{\tiny x}b{\tiny y}a{\tiny z}{\scriptsize\,-\,}b{\tiny x}b{\tiny y}tc{\tiny z}{\scriptsize\,+\,}b{\tiny x}b{\tiny y}ta{\tiny z}}{{\scriptsize\,-\,}b{\tiny x}a{\tiny y}z{\scriptsize\,+\,}b{\tiny x}a{\tiny y}a{\tiny z}{\scriptsize\,+\,}b{\tiny x}a{\tiny y}tc{\tiny z}{\scriptsize\,-\,}b{\tiny x}a{\tiny y}ta{\tiny z}}{{\scriptsize\,-\,}a{\tiny z}b{\tiny y}z{\scriptsize\,+\,}a{\tiny x}b{\tiny y}a{\tiny z}{\scriptsize\,+\,}a{\tiny z}b{\tiny y}tc{\tiny z}{\scriptsize\,-\,}a{\tiny x}b{\tiny y}ta{\tiny z}}{\scriptsize\,+\,}{a{\tiny x}a{\tiny y}z{\scriptsize\,-\,}a{\tiny x}a{\tiny y}a{\tiny z}{\scriptsize\,-\,}a{\tiny x}a{\tiny y}tc{\tiny z}{\scriptsize\,+\,}a{\tiny x}a{\tiny y}ta{\tiny z}}} \\ \small\textsf{以上の$3$つの式を連立方程式により媒介変数$t$を消去するわけだが、計算は至難の業である。文字式の限界といえよう。いずれにせよ、ここまでの手順で平面の式が求まる。} \end{array}\right\}\end{array}\right.\)
\(\textsf{任意の点と法線ベクトルよる平面の方程式}\)
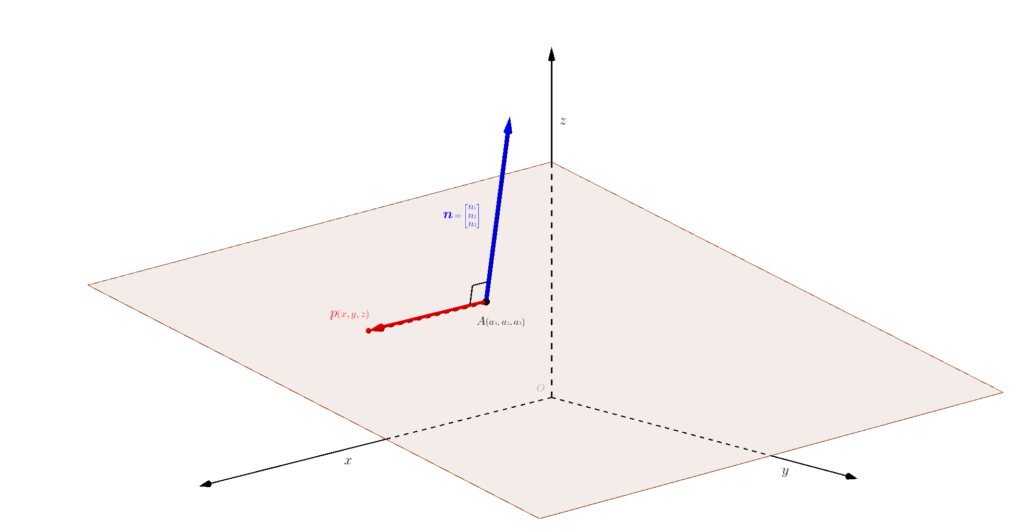
\(\textsf{図$2$から}\left\{\begin{array}{l}\textsf{平面の式は平面上の任意の点(ここでは$\color{red}p$)と同平面に垂直な$\href{https://showanojoe.com/template-math/linear-algebra/normal-vector-linear-equations/}{\textsf{法線ベクトル}}$($\color{blue}\boldsymbol n$)で求まる。} \\[5pt] \textsf{$\color{red}p$の座標成分を$\color{red}(x,y,x)$、法線ベクトル$\color{blue}\boldsymbol n$の成分を$\color{blue}\scriptsize\begin{bmatrix}n{\tiny 1} \\ n{\tiny 2} \\ n{\tiny 3}\end{bmatrix}$、点$A$(定点ではない)の座標成分を$(a{\tiny 1},a{\tiny 2},a{\tiny 3})$とする。} \\ \textsf{点$\color{red}p$から、平面と法線ベクトル$\color{blue}\boldsymbol n$の接点$A$までの$\LARGE\vec{\small A{\color{red}p}}$を置くとベクトルの内積より ${\color{blue}\boldsymbol n}\cdot{\LARGE\vec{\small A{\color{red}p}}}{\scriptsize\,=\,}0$ となる。} \\[5pt] \textsf{${\color{blue}\boldsymbol n}\cdot{\LARGE\vec{\small A{\color{red}p}}}{\scriptsize\,=\,}0$に各成分を代入して ${\color{blue}(n{\tiny 1},n{\tiny 2},n{\tiny 3})}\cdot({\color{red}x}{\scriptsize\,-\,}a{\tiny 1},{\color{red}y}{\scriptsize\,-\,}a{\tiny 2},{\color{red}z}{\scriptsize\,-\,}a{\tiny 3}){\scriptsize\,=\,}0\hspace{5pt}\rightarrow\hspace{5pt}{\color{blue}n{\tiny 1}}({\color{red}x}{\scriptsize\,-\,}a{\tiny 1}){\scriptsize\,+\,}{\color{blue}n{\tiny 2}}({\color{red}y}{\scriptsize\,-\,}a{\tiny 2}){\scriptsize\,+\,}{\color{blue}n{\tiny 3}}({\color{red}z}{\scriptsize\,-\,}a{\tiny 3}){\scriptsize\,=\,}0$} \\[5pt] \textsf{以上から、図$2$の平面の式は${\scriptsize\,-\,}{\color{blue}n{\tiny 1}}a{\tiny 1}{\scriptsize\,+\,}{\color{blue}n{\tiny 1}}{\color{red}x}{\scriptsize\,-\,}{\color{blue}n{\tiny 2}}a{\tiny 2}{\scriptsize\,+\,}{\color{blue}n{\tiny 2}}{\color{red}y}{\scriptsize\,-\,}{\color{blue}n{\tiny 3}}a{\tiny 3}{\scriptsize\,+\,}{\color{blue}n{\tiny 3}}{\color{red}z}{\scriptsize\,=\,}0$ を整理して ${\color{blue}n{\tiny 1}}{\color{red}x}{\scriptsize\,+\,}{\color{blue}n{\tiny 2}}{\color{red}y}{\scriptsize\,+\,}{\color{blue}n{\tiny 3}}{\color{red}z}{\scriptsize\,-\,}{\color{blue}n{\tiny 1}}a{\tiny 1}{\scriptsize\,-\,}{\color{blue}n{\tiny 2}}a{\tiny 2}{\scriptsize\,-\,}{\color{blue}n{\tiny 3}}a{\tiny 3}{\scriptsize\,=\,}0$ となる。}\end{array}\right.\)
