\(2\)次不等式を理解するための事前準備
\(\begin{array}{l}\textsf{不等式を理解するにあたっての 事前準備 がある。その事前準備とは \(2\)次方程式の理解 に他ならない。} \\[10pt] \hspace{10pt}\color{red}\underline{\color{black}\textsf{方程式とは、ザックリいうと 既知の数$(\textsf{係数、定数項})$と、文字で表した未知の数$(\textsf{変数$x,\,y$})$ の等式 である。}} \\[5pt] \hspace{10pt}{\color{gray}{\textsf{[事例]}}}\textsf{として、}\hspace{10pt} y{\small\,=\,}2x^2{\small \,+\,} 3x{\small \,+\,}4 \hspace{50pt}\left\{\begin{array}{l}\small\textsf{変数$\,x\,$によって$2$次式の値 $\,y\,$ が決まることはいうまでもない。} \\ \small\textsf{変数$x$の最高次が$2$次$(\textsf{$2$乗})$なので$2$次式という。}\end{array}\right\} \\[10pt] \textsf{変数$x,\,y$はもとより、係数$(\textsf{事例の$2,\,3$})$、定数項$(\textsf{事例の$4$。変数を含まない定数のみの項})$を文字で表した$2$次方程式$(\textsf{基本形の方程式という})$の表記は} \\[5pt] \hspace{200pt} \textsf{$\color{red}\underline{\color{black}y{\small\,=\,}ax^2{\small\,+\,}bx{\small\,+\,}c}$} \\[5pt] \hspace{300pt} \textsf{である。}\end{array}\)
解の公式
\(\begin{array}{l}\textsf{$2$次方程式では、解の公式 により解を求めることができる。} \\[10pt]\textsf{$\hspace{10pt}ax^2{\small\,+\,}bx{\small\,+\,}{\textsf{c}}{\small\,=\,}0$}\left\{\small\textsf{基本形の方程式 $y{\scriptsize\,=\,}ax^2{\scriptsize\,+\,}bx{\scriptsize\,+\,}c$ の変数 $y$ を移行して c${\scriptsize\,=\,}c{\scriptsize\,-\,}y$ とした方程式$ax^2{\small\,+\,}bx{\small\,+\,}{\textsf{c}}{\small\,=\,}0$ $(\textsf{これを一般形の方程式という})$。}\right\} \hspace{10pt}\textsf{の}\\[15pt] \hspace{100pt}\textsf{解の公式は}\hspace{10pt}{\boldsymbol{x{\small\,=\,}\small\displaystyle\frac{{\scriptsize \,-\,}b{\scriptsize\,\pm\,}\sqrt{\mathstrut{b^{2}{\tiny\,-\,}4a{\textsf{c}}}}}{2a}}}\hspace{10pt}\normalsize\textsf{となる。} \\[10pt] \hspace{200pt}\textsf{ただし、$\left\{\begin{array}{l}a{\small\,\neq\,}0 \:(\small\textsf{$a{\scriptsize\,=\,}0$ なら、$2$次方程式ではない。})\\[5pt] \textsf{$\small\sqrt{\mathstrut{b^{2}{\tiny\,-\,}4a{\textsf{c}}}}$ の $b^{2}{\small\,-\,}4a{\textsf{c}}$ は $b^{2}{\small\,-\,}4a{\textsf{c}}{\small\:\geqq\:}$0$\:(\color{red}\underline{\color{black}\small\textsf{ここは次節の 判別式 に紐付いている。})}$} \end{array}\right\}$ が条件。} \\[10pt]\hspace{100pt}\textsf{なお、係数$b$ が 偶数$(\textsf{特定の整数b とする})$ なら、} \\[10pt] \hspace{200pt}{\boldsymbol{x{\small\,=\,}\small\displaystyle\frac{{\scriptsize \,-\,}{\class{Boldfont}{\textsf{b}}}{\scriptsize\,\pm\,}\sqrt{\mathstrut{{\textsf{b}}^{2}{\tiny\,-\,}a{\textsf{c}}}}}{{a}}}}\hspace{10pt}\normalsize\textsf{の解の公式の 略式 が便利である。} \end{array}\)
判別式
\(\begin{array}{l}\textsf{$2$次方程式 $ax^2{\small\,+\,}bx{\small\,+\,}{\textsf{c}}{\small\,=\,}0$ の解$(\textsf{実数解})$は $2$つ、$1$つ$(\textsf{重解という})$、解なし$(\textsf{虚数解$2$つ。虚数解については省く})$ のいずれかである。} \\[10pt]\hspace{10pt} \textsf{これを判別するのに、判別式$(\small\textsf{$Discriminant$の頭文字をとって$D$と表記})$} \\[10pt]\hspace{100pt}D{\small\,=\,}b^{2}{\small\,-\,}4a{\textsf{c}} \hspace{10pt}\textsf{を用いる。} \\[10pt]\hspace{10pt}\textsf{b$(\small\textsf{$b$が偶数})$ならば、} \\[10pt]\hspace{100pt}D/4{\small\,=\,}{\textsf{b}}^{2}{\small\,-\,}a{\textsf{c}}\hspace{10pt}\textsf{を用いた方が便利である。}\hspace{50pt}\left\{\begin{array}{l}\small\textsf{$D/4$ これを 判別式$4$分の$D$ という。} \\ \small\textsf{b を 特定の整数 とする。} \\ \small\textsf{$b$が偶数なら、$b{\scriptsize\,=\,}2{\textsf{b}}(\textsf{偶数の定義は$2$の倍数である$(\textsf{特定の})$整数、ちなみに$0$も偶数である})$。} \\ \color{red}\underline{\color{black}b{\scriptsize\,=\,}2{\textsf{b}}\hspace{5pt}\rightarrow\hspace{5pt}{\textsf{b}}{\scriptsize\,=\,}{\scriptsize\displaystyle\frac{b}{2}}} \\ \small\textsf{$b^{2}{\scriptsize\,=\,}$$2$b${\scriptsize\,\times\,}$$2$b${\scriptsize\,=\,}4{\textsf{b}}^{2}$ から $\scriptsize\displaystyle\frac{4{\textsf{b}}^{2}{\scriptsize\,-\,}4a{\textsf{c}}}{4}$ を約分すると、$D/4{\scriptsize\,=\,}{\textsf{b}}^{2}{\tiny\,-\,}a{\textsf{c}}$ が成り立つ。}\end{array}\right\}\end{array}\)
判別式のグラフ
実数解\(2\)つ\(\hspace{15pt}D{\small\hspace{5pt}\gt\hspace{5pt}}0\)
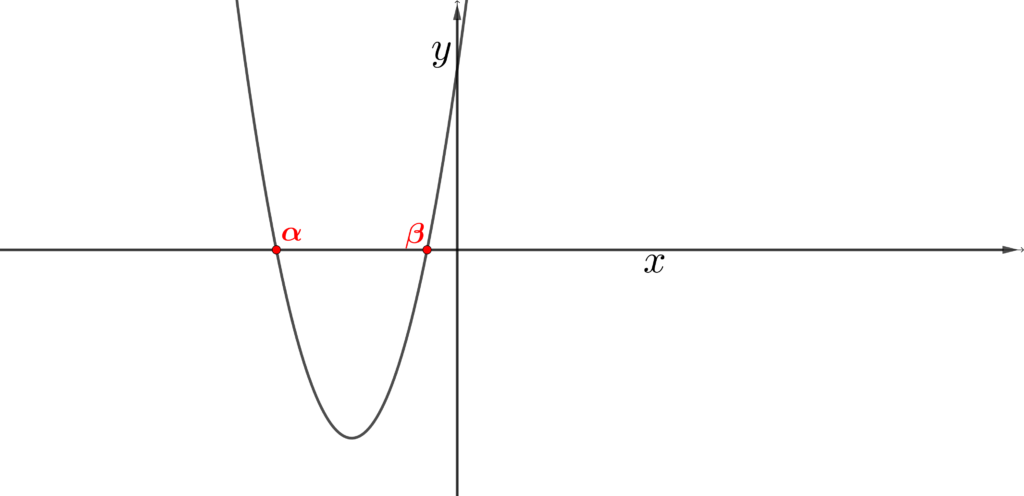
\(\hspace{30pt}\begin{array}{l}{\color{gray}\textsf{[事例]}} \\[10pt]{x^{2}{\small\,+\,}7x{\small\,+\,}6{\small\,=\,}0 \hspace{10pt}\textsf{の方程式の判別式}} \\[10pt] \hspace{10pt}\textsf{判別式 $D{\small\,=\,}b^{2}{\small\,-\,}4a{\textsf{c}}$ を用いると、} \\ \hspace{20pt}7^{2}{\small\,-\,}4\cdot 1\cdot 6{\small\hspace{10pt}\gt\hspace{5pt}}0\hspace{5pt}\textsf{ということになり、実数解が$2$つ$({\color{red}\alpha},\,{\color{red}\beta})$ ということになる。} \\[20pt] \textsf{なお、実数解${\color{red}\alpha},\,{\color{red}\beta}$ は $x^{2}{\small\,+\,}7x{\small\,+\,}6{\small\,=\,}0 $ を因数分解すると、$(x{\small\,+\,}1)(x{\small\,+\,}6){\small\,=\,}0$ になり、} \\ \hspace{10pt} x{\small\,=\,}{\small -}1,\,{\small -}6\hspace{5pt}({\href{https://showanojoe.com/template-math/supplementary-material/factor/#因数定理}{\textsf{因数定理}}\textsf{を参照}})\hspace{5pt}\textsf{ で ${\color{red}\alpha}{\small\,=\,}{\small -}6,\,{\color{red}\beta}{\small\,=\,}{\small -}1$ となる。}\end{array}\)
実数解\(1\)つ\(({\textsf{重解}})\hspace{15pt}D{\small\hspace{5pt}{\small\,=\,}\hspace{5pt}}0\,({\small D/4{\small\,=\,}0})\)

\(\hspace{30pt}\begin{array}{l}{\color{gray}\textsf{[事例]}} \\[10pt]{x^{2}{\small\,+\,}2x{\small\,+\,}1{\small\,=\,}0 \hspace{10pt}\textsf{の方程式の判別式}} \\[10pt] \hspace{10pt}\textsf{判別式 $D/4{\small\,=\,}{\textsf{b}}^{2}{\small\,-\,}a{\textsf{c}}$ を用いると、} \\ \hspace{20pt}1^{2}{\small\,-\,}1\cdot 1{\small\hspace{10pt}=\hspace{5pt}}0\hspace{5pt}\textsf{ということになり、実数解が$1$つ$({\color{red}\alpha}{\small\,=\,}{\color{red}\beta})$ ということになる。} \\[20pt] \textsf{なお、重解${\color{red}\alpha}{\small\,=\,}{\color{red}\beta}$ は $x^{2}{\small\,+\,}2x{\small\,+\,}1{\small\,=\,}0 $ を因数分解すると、$(x{\small\,+\,}1)(x{\small\,+\,}1){\small\,=\,}0\,\{{\scriptsize(x{\tiny\,+\,}1)^{2}{\tiny\,=\,}0}\}$ になり、} \\ \hspace{10pt} x{\small\,=\,}{\small -}1,\,{\small -}1\hspace{5pt}\hspace{5pt}\textsf{ で ${\color{red}\alpha}{\small\,=\,}{\small -}1,\,{\color{red}\beta}{\small\,=\,}{\small -}1$ となる。}\end{array}\)
解なし\(\hspace{15pt}D{\small\hspace{5pt}\lt\hspace{5pt}}0\)

\(\hspace{-30pt}\begin{array}{l}{\color{gray}\textsf{[事例]}} \\[10pt]{x^{2}{\small\,+\,}x{\small\,+\,}1{\small\,=\,}0 \hspace{10pt}\textsf{の方程式の判別式}} \\[10pt] \hspace{10pt}\textsf{判別式 $D{\small\,=\,}b^{2}{\small\,-\,}4a{\textsf{c}}$ を用いると、} \\ \hspace{20pt}1^{2}{\small\,-\,}4\cdot 1\cdot 1{\small\hspace{10pt}\lt\hspace{5pt}}0\hspace{5pt}\textsf{ということになり、$x(\textsf{軸})$との接点がない。} \\[10pt] {\color{gray}{\small -}x^{2}{\small -}x{\small -}1{\small\,=\,}0} \hspace{10pt}\textsf{の方程式の判別式} \\[10pt] \hspace{10pt}\textsf{判別式 $D{\small\,=\,}b^{2}{\small\,-\,}4a{\textsf{c}}$ を用いると、} \\ \hspace{20pt}({\small -}1)^{2}{\small\,-\,}4\cdot {\small -}1\cdot {\small -}1{\small\hspace{10pt}\lt\hspace{5pt}}0\hspace{5pt}\textsf{ということになり、$x(\textsf{軸})$との接点がない。} \\[15pt] \textsf{また、それぞれ$(x^{2}{\small\,+\,}x{\small\,+\,}1),\,({\color{gray}{\small -}x^{2}{\small -}x{\small -}1})$ より因数分解できない。} \end{array}\)
\(2\)次不等式
\(\begin{array}{l}\textsf{前節の $\href{#\(2\)次不等式を理解するための事前準備}{\textsf{$2$次不等式を理解するための事前準備 }}$では $2$次方程式 の 解の公式 と 判別式 を解説した。} \\ \hspace{10pt}\textsf{これを基に $2$次不等式 を解説しよう。} \\[10pt] \textsf{方程式の解答は実数解だが、不等式の解答は不等号を用いた大小関係の式になる。} \\[15pt] \hspace{50pt}\textsf{$2$次不等式の表記} \\[10pt]\hspace{150pt}{ax^{2}{\small\,+\,}bx{\small\,+\,}c{\small\:\geqq\:}0,\hspace{10pt}ax^{2}{\small\,+\,}bx{\small\,+\,}c{\small\:\lt\:}0}\end{array}\)
\(2\)次不等式のグラフ
\({ax^{2}{\small\,+\,}bx{\small\,+\,}c{\small\:\geqq\:}0,\hspace{10pt}ax^{2}{\small\,+\,}bx{\small\,+\,}c{\small\:\lt\:}0}\)

\(\hspace{20pt}\begin{array}{l}{\color{gray}\textsf{[事例]}} \\[10pt] \textsf{$2$次不等式$\hspace{5pt}x^{2}{\small\,+\,}7x{\small\,+\,}6{\small\,\geqq\,}0\hspace{5pt}$ の $x$ を求める。} \\[10pt] \hspace{10pt}\textsf{ $x^{2}{\small\,+\,}7x{\small\,+\,}6$ を因数分解して 境界点 を求める。} \\ \hspace{20pt}(x{\small\,+\,}1)(x{\small\,+\,}6)\hspace{5pt}\textsf{ということになり、境界点$\,{\color{red}\alpha}{\small\,=\,}{\small -}6,\,{\color{red}\beta}{\small\,=\,}{\small -}1$ ということになる。} \\[10pt] \hspace{10pt}\textsf{よって、${\color{red}\alpha}({\small{\scriptsize -}6})\:{\small\leqq}\:x\:{\small\leqq}\:{\color{red}\beta}({\small{\scriptsize -}1})$} \hspace{50pt}\left\{\small\textsf{境界点${\color{red}\alpha,\,\beta}$を含む$\color{red}\textsf{赤いエリア}$のすべての実数。}\right\} \\[10pt]\textsf{$2$次不等式$\hspace{5pt}x^{2}{\small\,+\,}7x{\small\,+\,}6{\small\,\lt\,}0\hspace{5pt}$ の $x$ を求める。} \\[10pt] \hspace{10pt}\textsf{ $x^{2}{\small\,+\,}7x{\small\,+\,}6$ を因数分解して 境界点 を求める。} \\ \hspace{20pt}(x{\small\,+\,}1)(x{\small\,+\,}6)\hspace{5pt}\textsf{ということになり、境界点$\,{\color{red}\alpha}{\small\,=\,}{\small -}6,\,{\color{red}\beta}{\small\,=\,}{\small -}1$ ということになる。} \\[10pt] \hspace{10pt}\textsf{よって、$x\:{\small\lt}\:{\color{red}\alpha}({\small{\scriptsize -}6}),\hspace{5pt}x\:{\small\gt}\:{\color{red}\beta}({\small{\scriptsize -}1})$} \hspace{50pt}\left\{\small\textsf{境界点${\color{red}\alpha,\,\beta}$を含まない$\color{gold}\textsf{黄色いエリア}$のすべての実数。}\right\}\end{array}\)
\({ax^{2}{\small\,+\,}bx{\small\,+\,}c{\small\:\gt\:}0,\hspace{10pt}ax^{2}{\small\,+\,}bx{\small\,+\,}c{\small\:\leqq\:}0}\)

\(\hspace{15pt}\begin{array}{l}{\color{gray}\textsf{[事例]}} \\[10pt] \textsf{$2$次不等式$\hspace{5pt}x^{2}{\small\,+\,}2x{\small\,+\,}1{\small\,\gt\,}0\hspace{5pt}$ の $x$ を求める。} \\[10pt] \hspace{10pt}\textsf{ $x^{2}{\small\,+\,}2x{\small\,+\,}1$ を因数分解して 境界点 を求める。} \\ \hspace{20pt}(x{\small\,+\,}1)^{2}\hspace{5pt}\textsf{ということになり、境界点$\,{\color{red}\alpha}{\small\,=\,}{\small -}1,\,{\color{red}\beta}{\small\,=\,}{\small -}1$ ということになる。} \\[10pt] \hspace{10pt}\hspace{10pt}\textsf{よって、$x\:{\small\lt}\:{\color{red}\alpha}({\small{\scriptsize -}1}),\hspace{5pt}x\:{\small\gt}\:{\color{red}\beta}({\small{\scriptsize -}1})$} \hspace{50pt}\left\{\small\textsf{境界点${\color{red}\alpha,\,\beta}$を含まない$\color{gold}\textsf{黄色いエリア}$のすべての実数。}\right\} \\[10pt] \hspace{10pt}\textsf{$2$次不等式$\hspace{5pt}x^{2}{\small\,+\,}2x{\small\,+\,}1{\small\,\leqq\,}0\hspace{5pt}$ の $x$ を求める。} \\[10pt] \hspace{10pt}\textsf{ $x^{2}{\small\,+\,}2x{\small\,+\,}1$ を因数分解して 境界点 を求める。} \\ \hspace{20pt}(x{\small\,+\,}1)^{2}\hspace{5pt}\textsf{ということになり、境界点$\,{\color{red}\alpha}{\small\,=\,}{\small -}1,\,{\color{red}\beta}{\small\,=\,}{\small -}1$ ということになる。} \\[10pt] \hspace{10pt}\textsf{よって、${\color{red}\alpha}({\small{\scriptsize -}1})\:{\small\leqq}\:x\:{\small\leqq}\:{\color{red}\beta}({\small{\scriptsize -}1})$} \hspace{50pt}\left\{\small\textsf{境界点${\color{red}\alpha,\,\beta}$となり、$x{\scriptsize\,=\,}{\scriptsize -}1。$}\right\}\hspace{10pt}\hspace{10pt}\end{array}\)
