極座標と極方程式

極座標

 極座標は極\((x,\,y\,\textsf{平面座標、または直交座標でいうところの原点})\)から座標点までの距離と方角を課題とした座標系である。

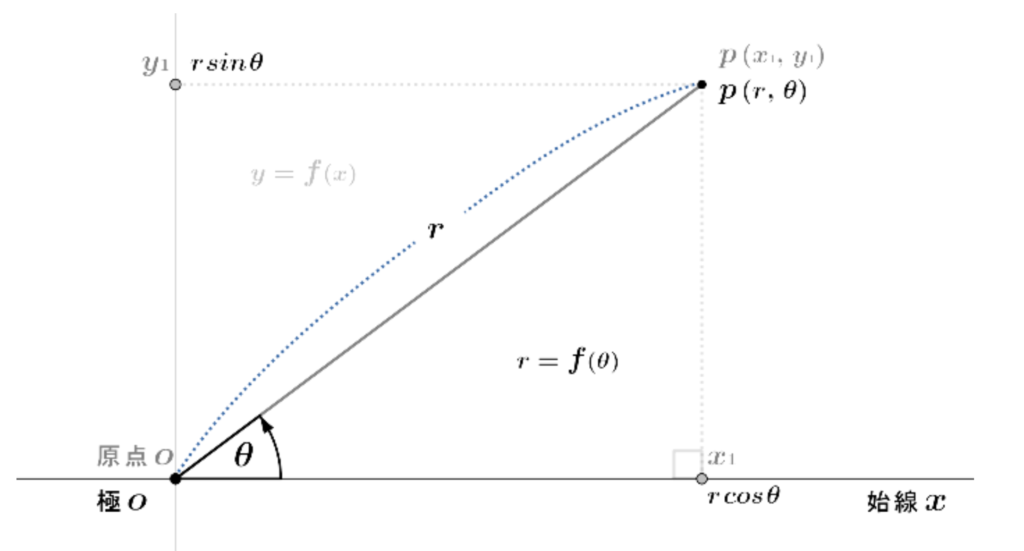
 図\(1\)で極座標と直交座標\((\textsf{グレーの表記})\)を比較した。
極\(\large o\)から座標点\(p\)までの距離\(\,\overline{op}{\small\,=\,}r\)、\(o\)から水平方向に始線\({\large x}(\textsf{直交座標の$x$軸})\)と\(\overline{op}\)が成す仰角は\(\theta\)。
直交座標の\(\color{gray}x{\tiny 1}\)を極座標に変換すると\(rcos\theta\)、\(\color{gray}y{\tiny 1}\)は\(rsin\theta\)。\(\hspace{15pt}\)☜ \(\href{https://showanojoe.com/template-math/trigonometric-function/extension-trigonometric-ratios/#1}{\color{teal}\textsf{単位円上の三角比}}\)の式変形
極座標点\(p\)の座標は\(p(r,\,\theta)\)となる。\(p(rcos\theta,\,rsin\theta)({\small\leftarrow}\;\textsf{これは極座標点を直交座標に変換した座標})\)ではないので注意 !

 \(3\)次元空間の全ての座標点を直交座標では \((x,\,y,\,z)\) の\(3\)変数で標記できる。
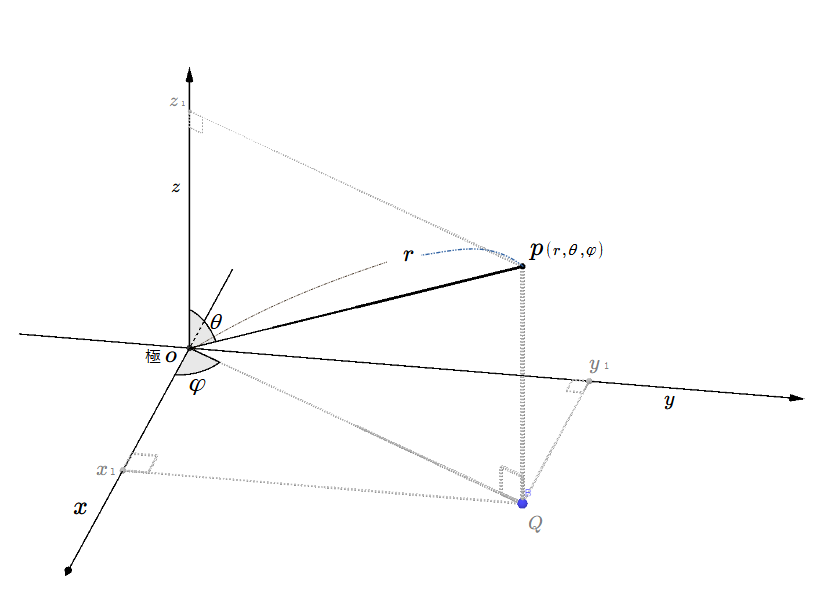
同様に、極座標の任意の座標点 \(p\) は \((r,\,\varphi,\,\theta)\) の\(3\)変数で表せる\((\small\textsf{図$2$})\)。これは地球上のある位置を特定する経緯度を連想させる。
つまり、\(r=\textsf{地球の半径}\)、\({\small\displaystyle\frac{\pi}{2}\,-\,}\theta=\textsf{緯度}\)、\(\varphi(\small\textsf{ファイ})=\textsf{経度}\)である。

 点\(p\)の極座標から直交座標への変換は、\(\left\{\begin{array}{l}{\color{gray}x{\tiny 1}}{\scriptsize\,=\,}rsin\theta cos\varphi \\ {\color{gray}y{\tiny 1}}{\scriptsize\,=\,}rsin\theta sin\varphi \\ {\color{gray}z{\tiny 1}}{\scriptsize\,=\,}rcos\theta \end{array}\right.\)   となる\((\small\textsf{以下の解説メモを参照})\)。

ちなみに、 経緯度から直交座標への変換はまた別の課題である。

\(2\)点間の距離

 平面の極座標

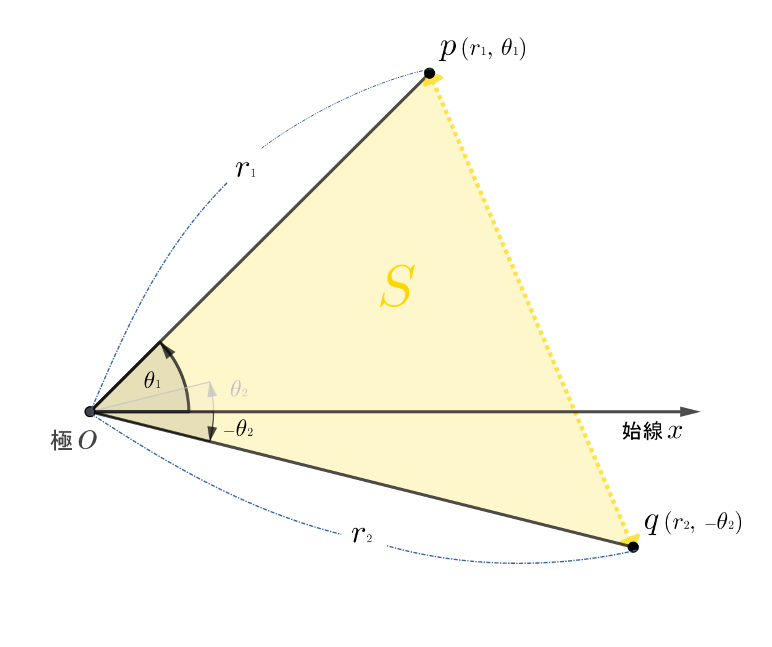
 \(\triangle opq\) の面積\(\color{gold}S\)を考慮して、

\(\measuredangle{poq}\)\({\scriptsize\,=\,}\theta{\tiny 1}{\boldsymbol\scriptsize -}({\scriptsize -}\theta{\tiny 2})\)\(\hspace{15pt}\)\({\lbrace}\)\({\small\leftarrow} \hspace{5pt}\)\(|\theta{\tiny 1}{\scriptsize\,+\,}{\small |}{\scriptsize -}\theta{\tiny 2}{\small |}|\) ということだが、\(2\)重絶対値はややっこしいので演算子を \(\boldsymbol{-}\) にする\(|\theta{\tiny 1}{\boldsymbol\scriptsize -}({\scriptsize -}\theta{\tiny 2})|\)。\(\href{https://showanojoe.com/template-math/trigonometric-function/extension-trigonometric-ratios/#1}{\color{teal}{cos(\theta{\tiny 1}{\small -}({\scriptsize -}\theta{\tiny 2})){\small\,=\,}cos(({\scriptsize-}\theta{\tiny 2}){\small -}\theta{\tiny 1})}}\) なので 絶対値が不要となり \(\theta{\tiny 1}{\boldsymbol\scriptsize -}({\scriptsize -}\theta{\tiny 2})\)。\(\rbrace\)

\(\overline{op}{\scriptsize\,=\,}r{\tiny 1}\)\(,\,\overline{oq}{\scriptsize\,=\,}r{\tiny 2}\)

以上の提示から 三角関数の\(\href{https://showanojoe.com/template-math/trigonometric-function/cosine-theorem/}{\color{teal}\textsf{余弦定理}}\)で図\(3\)の \(2\)点間の距離 \(\overline{pq}\) が求められる。

\[(\overline{pq})^{\scriptsize 2}{\scriptsize\;=\,}r{\tiny 1}^{\scriptsize 2}{\scriptsize\;+\;}r{\tiny 2}^{\scriptsize 2}{\scriptsize\;-\;}2r{\tiny 1}r{\tiny 2}\,cos(\theta{\tiny 1}{\small -}({\scriptsize -}\theta{\tiny 2})){\small\hspace{10pt}\rightarrow\hspace{10pt}}\overline{op}{\scriptsize\;=\;}\sqrt{r{\tiny 1}^{\scriptsize 2}{\scriptsize\;+\;}r{\tiny 2}^{\scriptsize 2}{\scriptsize\;-\;}2r{\tiny 1}r{\tiny 2}\,cos(\theta{\tiny 1}{\small -}({\scriptsize -}\theta{\tiny 2}))}\]

 \(3\)次元空間の極座標

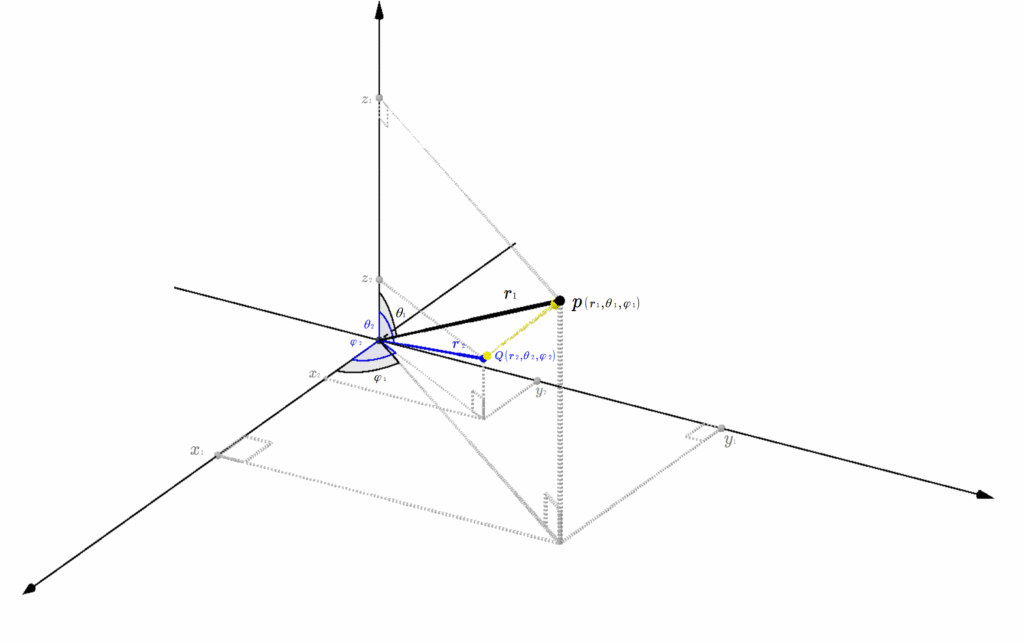
\[\overline{op}{\scriptsize\;=\;}\sqrt{r{\tiny 1}^{\scriptsize 2}{\scriptsize\,+\,}r{\tiny 2}^{\scriptsize 2}{\scriptsize\,-\,}2r{\tiny 1}r{\tiny 2}\lbrace cos(\varphi{\tiny 1}{\scriptsize\,-\,}\varphi{\tiny 2})sin\theta{\tiny 1}sin\theta{\tiny 2}{\scriptsize\,+\,}cos\theta{\tiny 1}cos\theta{\tiny 2}}\]

極方程式

 平面の極座標 \((r,\,\theta)\)、\(3\)次元空間の極座標 \((r,\,\varphi,\,\theta)\) にある点が描く軌跡\((\)図形\()\)を 関数 \(r{\small\;=\;}{\large f}{\small(\theta)}\)、\(r{\small\;=\;}{\large f}{\small(\varphi,\,\theta)}\) に従って表した方程式を \({}^{\scriptsize {“}}\,\textsf{極方程式}^{\,\scriptsize{”}}\) という。

\(\color{gray}[\textsf{事例$1$}]\)

図\(1\)の直線 \(\color{red}l\) の極方程式を求めてみる。

\(\color{gray}[\textsf{事例$2$}]\)

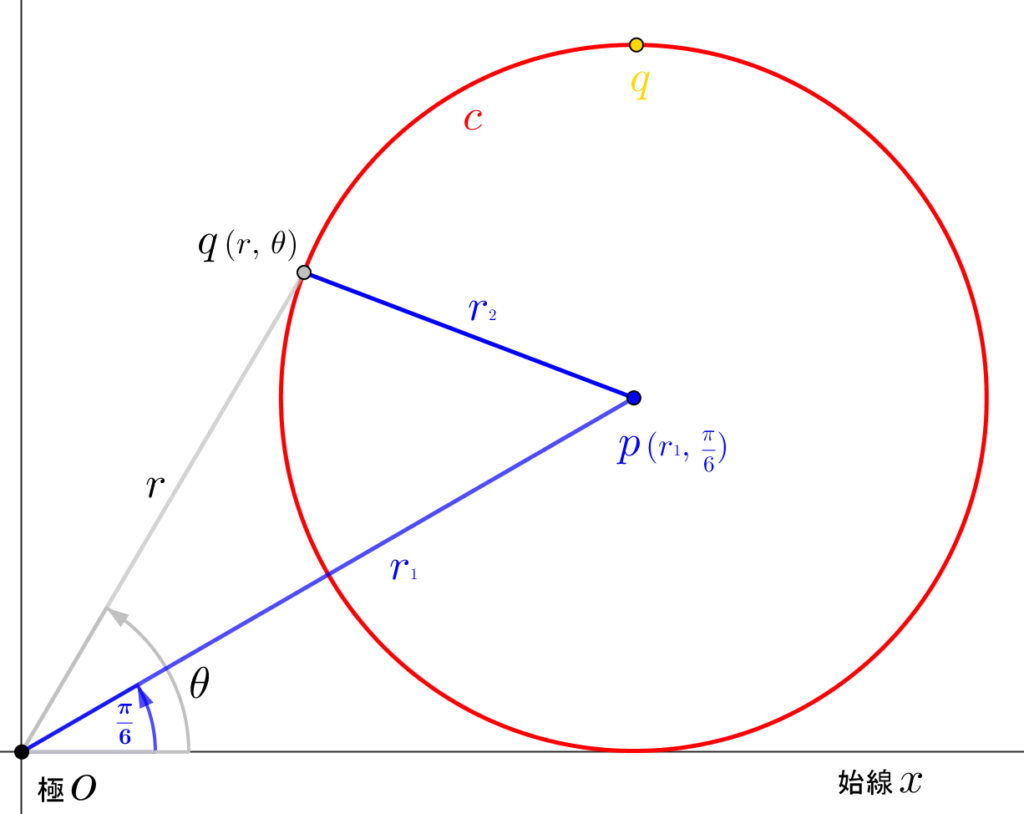
 図\(2\)の円 \(\color{red}C\) の極方程式を求めてみる。