集合の表記
集合は要素が含まれる範囲を課題とする。
集合に要素が含まれる

\(\begin{array}{l}\textsf{$a{\tiny 1},\,a{\tiny 2},\,a{\tiny 3}$ は集合$A$に含まれる$(\textsf{という記号})$。} \\[5pt] \hspace{20pt}a{\tiny 1}\in A,\:a{\tiny 2}\in A,\:a{\tiny 3}\in A \hspace{50pt}\left\{\small\textsf{$a{\tiny 4}$は集合$A$には含まれないので、$a{\tiny 4}\notin A$と表記される。}\right\} \\[5pt]\textsf{これは、集合$A$は要素$a{\tiny 1},\,a{\tiny 2},\,a{\tiny 3}$を含むということで、} \\[5pt] \hspace{20pt}A{\small\,=\,}\{a{\tiny 1},\,a{\tiny 2},\,a{\tiny 3}\} \\[5pt]\textsf{と表記される。}\hspace{50pt}\left\{\small\textsf{ちなみに集合の作図$(\textsf{左図})$を ベン図 という。}\right\}\end{array}\)
部分集合
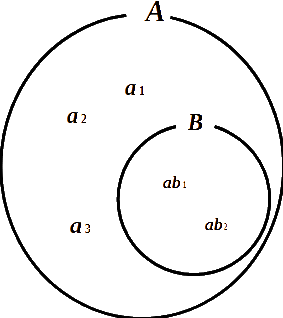
\(\begin{array}{l}\textsf{集合$A$に集合$B$が含まれる。} \\[5pt]\hspace{20pt}B\subset A\end{array}\)
共通部分集合
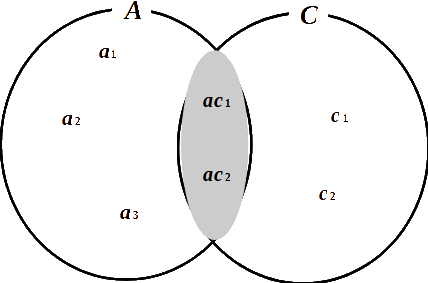
\(\begin{array}{l}\textsf{集合$A$と集合$C$の共通部分をいう。} \\[5pt]\hspace{20pt}A\cap C \\[5pt]\textsf{左図では要素 $ac{\scriptsize 1},\,ac{\scriptsize 2}$ を囲む灰色の部分。}\end{array}\)
和集合
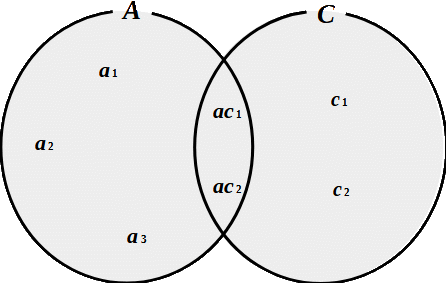
\(\begin{array}{l}\textsf{集合$A$と集合$C$に含まれる要素全体の集合。} \\[5pt]\hspace{20pt}A\cup C \\[5pt]\textsf{左図では $A\cup C{\small\,=\,}\left\{a{\scriptsize 1},\,a{\scriptsize 2},\,a{\scriptsize 3},\,ac{\scriptsize 1},\,ac{\scriptsize 2},\,c{\scriptsize 1},\,c{\scriptsize 2}\right\}$}\end{array}\)
空くう集合と補集合
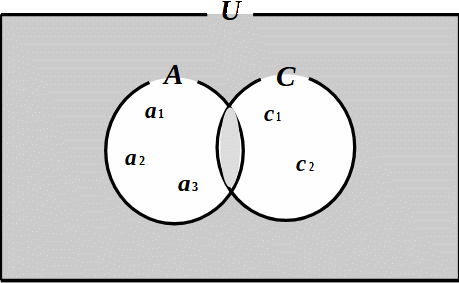
\(\begin{array}{l}\textsf{集合$A,\,C$を含む 全体集合 を$U$とする。} \\[5pt]\hspace{20pt}A\cap C{\small\,=\,}\phi\hspace{50pt}\left\{\begin{array}{l}\small\textsf{$A\cap C{\scriptsize\,=\,}\{\}$で要素がカラなので$\phi(\textsf{ファイ})$と表記し、} \\ \small\textsf{空集合という。}\end{array}\right\} \\[5pt]\textsf{また、全体集合$U$に含まれる要素で集合$A,\,C$に属さない要素の集合$(\textsf{補集合})$は} \\[5pt]\hspace{20pt}\overline{A\cup C}\subset U\hspace{50pt}\left\{\small\textsf{アンダーバーの部分が補集合を表す。}\right\} \\[5pt]\textsf{と表記される。左図では $\overline{A\cup C}\subset U{\small\,=\,}\phi$ となる。}\end{array}\)
