三角形の度数法を 弧度法 で表記することで、三角比を拡張した三角関数の 解析 を計る。
単位円と三角比
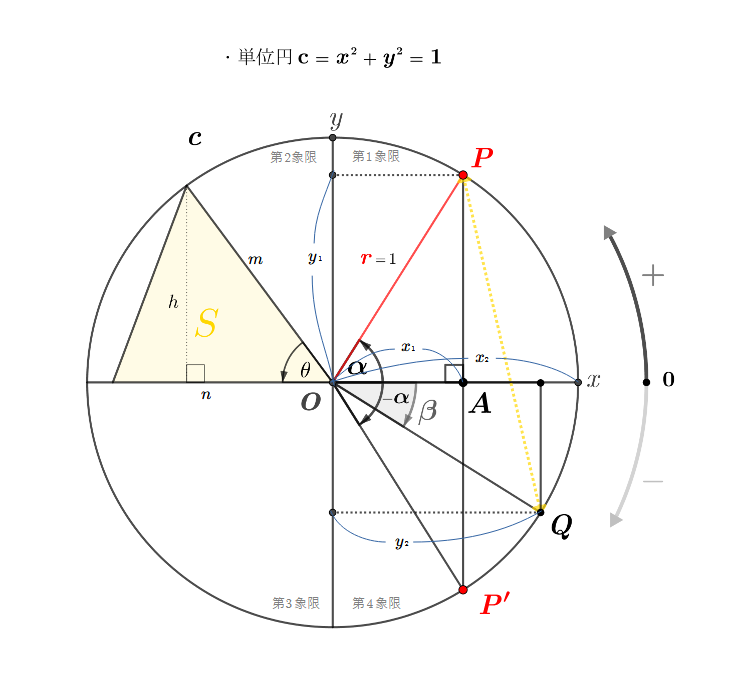
以下、図\(1\)の解説。
平面において \(2\)直線の交点を中心に\(2\)直線に仕切られた\(4\)つの部分を象限という。
四分儀を定義する直交座標軸 \({\large o}-xy\) で分けた場合は∠xOyの内部を第1象限といい,以下反時計回りに,∠yOx′,∠x′Oy′,∠y′Oxの内部を第2,3,4象限という。空間を互いに交わる2平面で4部分に分けたときも各部分空間を象限という。
二点間の距離を \(\href{https://showanojoe.com/template-math/trigonometric-function/three-squares-theorem/}{\textsf{三平方の定理}}\) で表すと、
中心点\(\Large o\)から単位円周上の点\(\color{red}P\) までの距離\(\hspace{15pt}O{\color{red}P}{\small\,=\,}\sqrt{\mathstrut{x\tiny1}^{\tiny 2}+{y\tiny1}^{\tiny 2}}\)\(\hspace{10pt}{\small\rightarrow}\hspace{10pt}({\scriptsize ={\color{red}\small r}=1})\)
単位円周上の二点 \(\color{red}P\)、\(Q\)間の距離 \(\hspace{15pt}{\color{red}P}{ Q}=\sqrt{\mathstrut{({x\tiny1}-{x\tiny2})^{\tiny 2} + ({y\tiny1}-{y\tiny2})^{\tiny 2}}}\)
\(\measuredangle{\alpha}\) がなす \(\varDelta O\!A{\color{red}P}\) の単位円上の三角比
\(\left\{\begin{array}{l}cos{\large\alpha}{\,\small =\,}{\displaystyle\frac{x \tiny 1}{\color{red}r}}{\,\small =\,}{\displaystyle\frac{x\tiny{1}}{\small 1}}{\,\small =\,}{\large x \tiny 1} \\[2pt] cos({{\small-}\alpha}){\,\small =\,}{\displaystyle\frac{x \tiny 1}{\color{red}r}}{\,\small =\,}{\displaystyle\frac{x\tiny{1}}{\small 1}}{\,\small =\,}{\large x \tiny 1} \\[2pt] sin{\large\alpha}{\,\small =\,}{\displaystyle\frac{y\tiny 1}{\color{red}r}}{\,\small =\,}{\displaystyle\frac{y\tiny{1}}{\small 1}}{\,\small =\,}{\large y \tiny 1} \\[2pt]tan{\large\alpha}{\,\small =\,}{\displaystyle\frac{y \tiny 1}{x \tiny 1}} \end{array}\right. \)
\(\varDelta O\!A{\color{red}P}\)\((\)直角三角形\()\)の\(\cssId{1}{\textsf{三角比の相互関係式}}\)
\(\left\{\begin{array}{l}{cos}^{2}\large\alpha{\,\small +\,}{\normalsize sin}^{\small 2}\large\alpha{\,\small =\,}{\class{Underline}{{x\tiny 1}^{\small 2}{\,\small +\,}{y \tiny 1}^{\small 2}{\,\small =\,}{\color{red}\Large r}^{\small 2}}}{\small\,=\,}1 \\ \normalsize{tan}{\large\alpha}{\,\small =\,}\small\displaystyle\frac{sin\normalsize\alpha}{cos\normalsize\alpha}\color{gray}\hspace{20pt}cf\;{\small\rightarrow}\hspace{5pt}\normalsize{tan^{2}}{\large\alpha}{\,\small =\,}\small\displaystyle\frac{sin^{2}\normalsize\alpha}{cos^{2}\normalsize\alpha} \\ 1{\,\small +\,}tan^{\small 2}{\large\alpha}{\,\small =\,}\small\displaystyle\frac{cos\normalsize\alpha}{cos\normalsize\alpha}{\,\small +\,}\left(\small\displaystyle\frac{sin\normalsize\alpha}{cos\normalsize\alpha}\right)^{\small 2} \\ \hspace{10pt}{\,\small =\,}\small\displaystyle\frac{cos\normalsize\alpha}{cos\normalsize\alpha}{\,\small +\,}\small\displaystyle\frac{sin^{\small 2}\normalsize\alpha}{cos^{\small 2}\normalsize\alpha}{\,\small =\,}\small\displaystyle\frac{{cos^{\small 2}\normalsize\alpha}{\,\small +\,}{sin^{\small 2}\normalsize\alpha}}{cos^{\small 2}\normalsize\alpha} \\ \hspace{20pt}{\,\small =\,}\small\displaystyle\frac{1}{cos^{\small 2}\normalsize\alpha}\end{array}\right.\)
\(x\) 軸に関する \(\varDelta O\!A{\color{red}P}\) の鏡映\(\varDelta O\!A{\color{red}P^{\prime}}\)の三角比
\(cos({\small -}{\large\alpha}){\,\small =\,}{\displaystyle\frac{x \tiny 1}{\color{red}r}}{\,\small =\,}{\displaystyle\frac{x\tiny{1}}{\small 1}}{\,\small =\,}{\large x \tiny 1}\)
\(sin({\small -}{\large\alpha}){\,\small =\,}{\displaystyle\frac{-y\tiny 1}{\color{red}r}}\)\({\,\small =\,}{\displaystyle\frac{-y\class{Millifont}{1}}{\small 1}}\)\({\,\small =\,}{-\large y \tiny 1}tan({\small -}{\large\alpha}){\,\small =\,}{\displaystyle\frac{-y \tiny 1}{x \tiny 1}}\)
\(\triangle{\color{gold}S}\) の面積は \({\small\displaystyle\frac{1}{2}}m{\small |}n{\small |}\,sin\theta\) で求まる。
\(m{\small\;=\,}r\)、\(n\) は\(x\)軸の\(-\)方向にあるので\(\href{https://showanojoe.com/template-math/supplementary-material/absolute-value/}{\color{teal}\textsf{絶対値}}\)をつける\((\)面積に\(-\)符号はありえないので\()\)。
\(sin\theta{\small\;=\,}{\small\displaystyle\frac{h}{m}}\)、\(m{\small\;=\,}r{\small\;=\,}1\) なので、 \(sin\theta{\small\;=\,}h\) \(h\) は\(y\)軸の\(+\)方向にあるので第\(2\)象限にある三角形は絶対値が不要となる。
弧度法
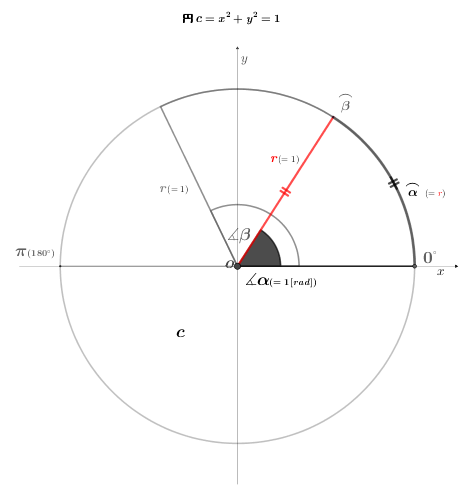
弧度法とは、\(\color{red}\underline{\color{black}\textsf{円の半径と弧長が等しい扇形の中心角の大きさ}}\) を定義とした表記法である。
弧度法の単位は \({\small [rad]}({\small\textsf{ラジアン}})\textsf{だが、慣習的に省略される。}\)
度数法の中心角\(180^{\circ}\)を弧度法では\(\pi\)と表記する理由を以下で解説する。
\(\measuredangle{\alpha} =1{\small [rad]}{\scriptsize(1[rad]=\,57.29578^{\circ})}\) とすると、
\(\textsf{弧長}\stackrel{\textstyle\frown}{\mathrm{\alpha}}\;{\small =}\;\left\{{2}\pi{\color{red} r} \left( \small\textsf{円周の長さの定義} \right) \times {\small \displaystyle\frac{\alpha}{360}} \left({\small\textsf{ 中心角360°に、扇形の中心角 }}\measuredangle{\alpha} \textsf{が占める割合}\right)\right\}
\;{\small =}\;{\color{red}\large r}\)\(\hspace{10pt}\Rightarrow\hspace{5pt}{\small \displaystyle\frac{\alpha\,\pi \color{red}r}{180^\circ}}= {\large\color{red} r}\)
それで、\(\textsf{${\small \displaystyle\frac{\alpha\,\pi \color{red}r}{180^\circ}}\;{\small =}\;{\large\color{red} r}$ の両辺に $\frac{180^\circ}{\pi}$ を掛けて式変形すると、}\)
\(\Rightarrow\hspace{5pt} \alpha\,{\color{red}r} ={\small \displaystyle\frac{180^\circ\, \color{red}r}{\pi}} \Rightarrow\,\alpha={\small \displaystyle\frac{180^\circ}{\pi}} \hspace{10pt}\Rightarrow\,\measuredangle{\alpha}=1{\color{lightgray}\small [rad]}={\small \displaystyle\frac{180^\circ}{\pi}}\)
以上から、\(1{\scriptsize\,=\,\displaystyle\frac{180^\circ}{\pi}}\)なので、分母の \(\normalsize\pi\) は \(180^{\circ}\) といえる。
ちなみに、弧度法の定義でいう \(\measuredangle{\beta}\) は \(\beta{\scriptsize\color{black}[rad]}\)となる。
上述したように弧度法の単位\((\measuredangle{\alpha}\textsf{で示した}[rad])\)は省略の対象となり、度数法の中心角\(\pi\,180^{\circ}\)が弧度法に変換されて本来 円周率の記号である\(\pi\)を用いる。三角比の拡張は弧度法の \(\pi\)が基準 となる。
\(\class{Boldfont}{\textsf{$\measuredangle{\alpha}$ の三角比の拡張}}\)
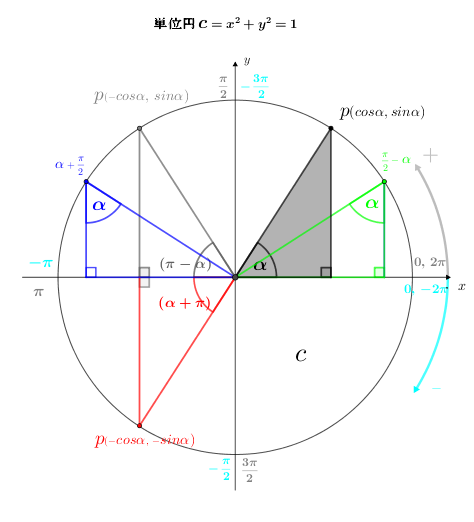
\(\measuredangle{\large\alpha}\:\left\{\begin{array}{l}\:\textsf{がなす(直角)三角形$ \textsf{の斜辺は $r=1$ なので、}\left\{\begin{array}{l} cos{\large\alpha}=\small{\displaystyle{\frac{x}{1}}}={{\large x}(\textsf{軸の座標})} \\ sin{\large\alpha}=\small{\displaystyle{\frac{y}{1}}}={{\large y}(\textsf{軸の座標})}\end{array}\right\}$で、単位円 ${\bf\it\large c}$ の円周上の点 ${\large p}$ の座標は $(cos{\large\alpha},\,sin\large\alpha)$ となる。}\\[5pt] \:\textsf{がなす(直角)三角形の} tan{\large\alpha}=\displaystyle{\frac{y}{x}}。\\[5pt] \: \textsf{がなす(直角)三角形の}\left\{\begin{array}{l}cos({\color{gray}\pi-\alpha}) = -cos{\large\alpha},\hspace{10pt}sin({\color{gray}\pi-\alpha}) = sin{\large\alpha},\hspace{10pt}tan({\color{gray}\pi-\alpha}) = -tan{\large\alpha} \\[10pt]cos({\color{red}\alpha+\pi})=-cos{\large\alpha},\hspace{10pt}sin({\color{red}\alpha+\pi})=-sin{\large\alpha},\hspace{10pt}tan({\color{red}\alpha+\pi})=tan{\large\alpha} \\[10pt]cos({\color{blue}\alpha+\small\displaystyle\frac{\pi}{2}})=-sin{\large\alpha},\hspace{10pt}sin({\color{blue}\alpha+\small\displaystyle\frac{\pi}{2}})=cos{\large\alpha},\hspace{10pt}tan({\color{blue}\alpha+\small\displaystyle\frac{\pi}{2}})=-\small\displaystyle\frac{1}{tan{\normalsize\alpha}} \\[10pt]cos({\color{springgreen}\small\displaystyle\frac{\pi}{2}-\alpha})=sin{\large\alpha},\hspace{10pt}sin({\color{springgreen}\small\displaystyle\frac{\pi}{2}-\alpha})=cos{\large\alpha},\hspace{10pt}tan({\color{springgreen}\small\displaystyle\frac{\pi}{2}-\alpha})=\small\displaystyle\frac{1}{tan{\normalsize\alpha}} \end{array}\right. \end{array}\right. \)
グラフで三角比を表記
図3 \(\measuredangle{\alpha}\)の三角比の拡張 の円弧矢印で表示した反時計回り、時計回りを参照
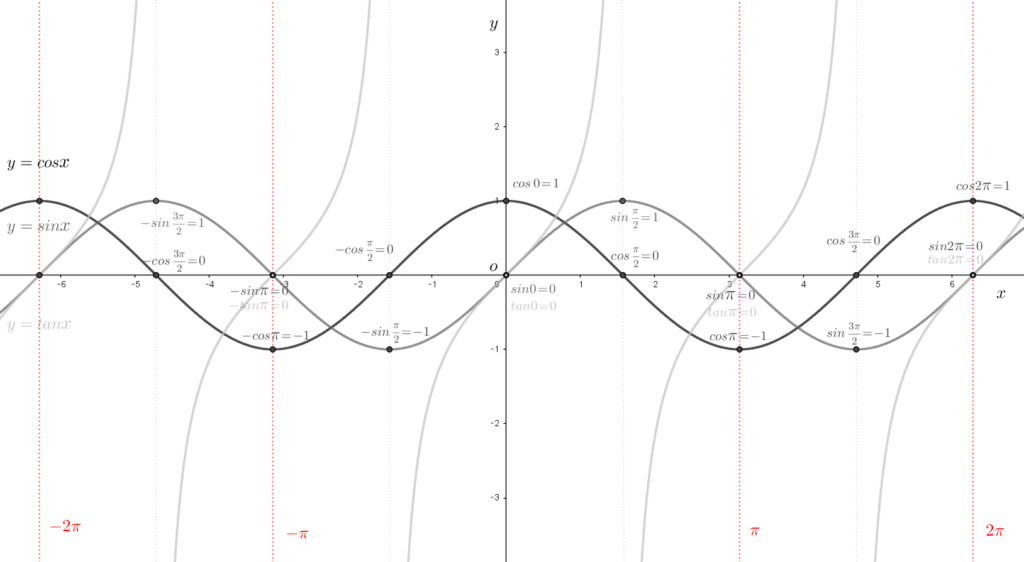
三角比の還元\((\small\textsf{変換})\)公式
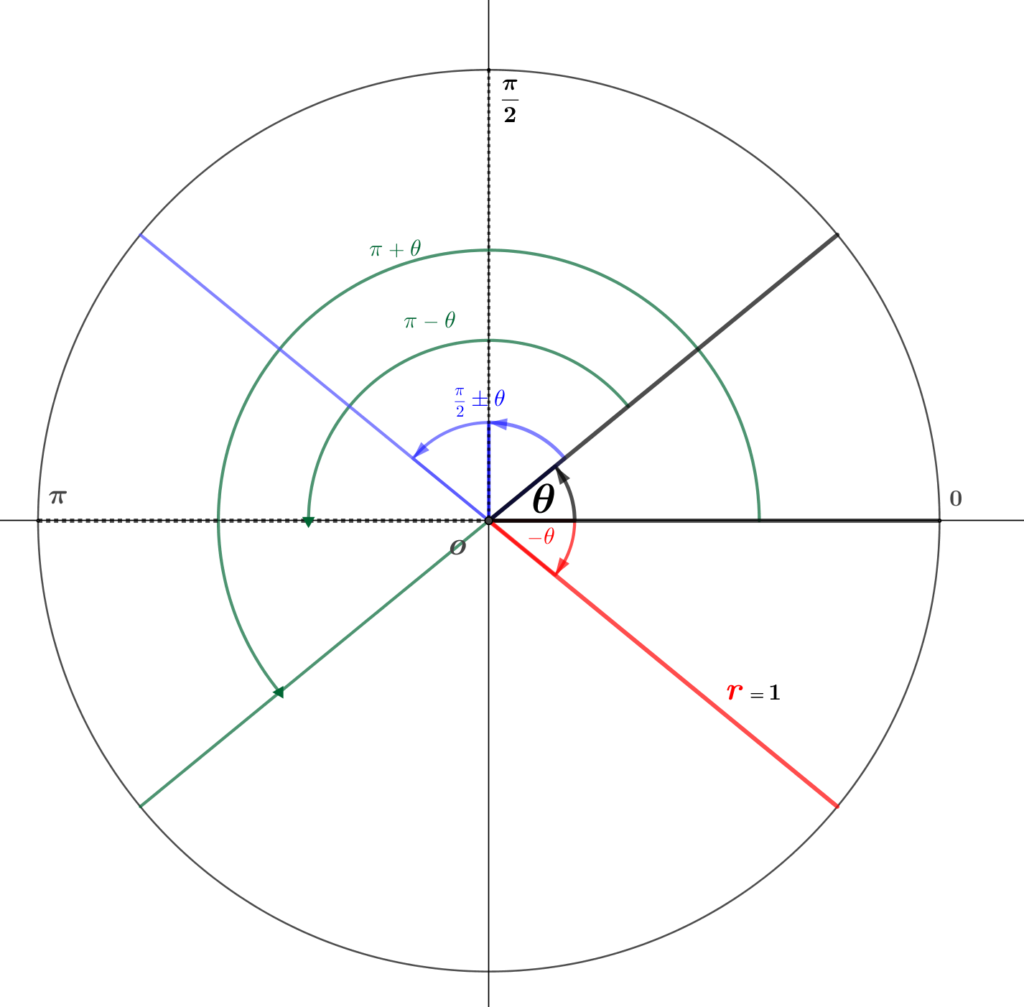
負角 \({\color{red}{\measuredangle 0-\theta}}\,({\small \measuredangle{\small -}\theta=\measuredangle\alpha+\measuredangle\beta \,\textsf{とすると、$\measuredangle\alpha=0,\,\measuredangle\beta=-\theta$ の角}})\)
\(\left\{\begin{array}{l}cos(-\theta){\,\small =\,}{\class{Underline-L}{cos(0{\small -}\theta){\,\small =\,}cos0 cos\theta{\,\small +\,}sin0 sin\theta{\,\small =\,}cos{\small\displaystyle\frac{1}{1}}cos\theta{\,\small +\,}sin{\small\displaystyle\frac{0}{1}}sin\theta}}{\,\small =\,}\hspace{20pt}cos\theta \hspace{20pt}\left\{\small\textsf{加法定理による導出。}\right\} \\[5pt] sin({\small -}\theta){\,\small =\,}{\class{Underline-L}{sin(0-\theta){\,\small =\,}sin0 cos\theta{\,\small -\,}cos0 sin\theta{\,\small =\,}cos{\small\displaystyle\frac{1}{1}}cos\theta{\,\small +\,}sin{\small\displaystyle\frac{0}{1}}sin\theta}}{\,\small =\,}-sin\theta \hspace{20pt}\left\{\small\textsf{加法定理による導出。}\right\} \\[5pt] tan({\small -}\theta){\,\small =\,}{\class{Underline-L}{{\small\displaystyle\frac{sin(-\theta)}{cos(-\theta)}}{\,\small =\,}{\small\displaystyle\frac{-sin\theta}{cos\theta}}}}{\,\small =\,}-tan\theta\hspace{20pt}\left\{\small\textsf{三角関数の相互関係式と上記の還元公式より導出。}\right\} \end{array}\right.\)
余角 \({\color{blue}\measuredangle {\small\displaystyle\frac{\pi}{2}}\pm\theta}\,({\small \measuredangle{\scriptsize\displaystyle\frac{\pi}{2}}\pm\theta=\measuredangle\alpha+\measuredangle\beta\, \textsf{とすると、 $\measuredangle\alpha={\small\displaystyle\frac{\pi}{2}},\,\measuredangle\beta=\pm\theta$ の角}})\)
\(\left\{\begin{array}{l} cos({\small\displaystyle\frac{\pi}{2}}+\theta){\,\small =\,}{\class{Underline-L}{cos{\small\displaystyle\frac{\pi}{2}} cos\theta{\,\small -\,}sin{\small\displaystyle\frac{\pi}{2}} sin\theta{\,\small =\,}cos{\small\displaystyle\frac{0}{1}}cos\theta{\,\small -\,}sin{\small\displaystyle\frac{1}{1}}sin\theta}}{\,\small =\,}-sin\theta \hspace{20pt}\left\{\small\textsf{加法定理による導出。}\right\} \\[5pt] cos({\small\displaystyle\frac{\pi}{2}}-\theta){\,\small =\,}{\class{Underline-L}{cos{\small\displaystyle\frac{\pi}{2}} cos\theta{\,\small +\,}sin{\small\displaystyle\frac{\pi}{2}} sin\theta{\,\small =\,}cos{\small\displaystyle\frac{0}{1}}cos\theta{\,\small +\,}sin{\small\displaystyle\frac{1}{1}}sin\theta}}{\,\small =\,}\hspace{20pt}sin\theta \hspace{20pt}\left\{\small\textsf{加法定理による導出。}\right\} \\[5pt] sin({\small\displaystyle\frac{\pi}{2}}+\theta){\,\small =\,}{\class{Underline-L}{sin{\small\displaystyle\frac{\pi}{2}} cos\theta{\,\small +\,}cos{\small\displaystyle\frac{\pi}{2}} sin\theta{\,\small =\,}cos{\small\displaystyle\frac{1}{1}}cos\theta{\,\small +\,}sin{\small\displaystyle\frac{0}{1}}sin\theta}}{\,\small =\,}\hspace{20pt}cos\theta \hspace{20pt}\left\{\small\textsf{加法定理による導出。}\right\} \\[5pt] sin({\small\displaystyle\frac{\pi}{2}}-\theta){\,\small =\,}{\class{Underline-L}{sin{\small\displaystyle\frac{\pi}{2}} cos\theta{\,\small -\,}cos{\small\displaystyle\frac{\pi}{2}} sin\theta{\,\small =\,}cos{\small\displaystyle\frac{1}{1}}cos\theta{\,\small -\,}sin{\small\displaystyle\frac{0}{1}}sin\theta}}{\,\small =\,}\hspace{20pt}cos\theta \hspace{20pt}\left\{\small\textsf{加法定理による導出。}\right\} \\[5pt] tan(\small\displaystyle\frac{\pi}{2}+\theta){\,\small =\,}{\class{Underline-L}{{\small\displaystyle\frac{sin(\small\displaystyle\frac{\pi}{2}+\theta)}{cos(\small\displaystyle\frac{\pi}{2}+\theta)}}{\,\small =\,}{\small\displaystyle\frac{cos\theta}{-sin\theta}}}}{\,\small =\,}-\small\displaystyle\frac{1}{tan}\hspace{20pt}\left\{\small\textsf{三角関数の相互関係式と上記の還元公式より導出。}\right\} \\[5pt] tan(\small\displaystyle\frac{\pi}{2}-\theta){\,\small =\,}{\class{Underline-L}{{\small\displaystyle\frac{sin(\small\displaystyle\frac{\pi}{2}-\theta)}{cos(\small\displaystyle\frac{\pi}{2}-\theta)}}{\,\small =\,}{\small\displaystyle\frac{cos\theta}{sin\theta}}}}{\,\small =\,}\small\displaystyle\frac{1}{tan}\hspace{20pt}\left\{\small\textsf{三角関数の相互関係式と上記の還元公式より導出。}\right\} \end{array}\right.\)
補角 \({\color{teal}\measuredangle \pi-\theta}\,({\small \measuredangle \pi{\small -}\theta=\measuredangle\alpha+\measuredangle\beta \textsf{とすると、$\measuredangle\alpha=\pi,\,\measuredangle\beta=\pm\theta$ の角}})\)
\(\left\{\begin{array}{l} cos(\pi+\theta){\,\small =\,}{\class{Underline-L}{cos{\small\pi} cos\theta{\,\small -\,}sin\pi sin\theta{\,\small =\,}cos{\small\displaystyle\frac{-1}{1}}cos\theta{\,\small -\,}sin{\small\displaystyle\frac{0}{1}}sin\theta}}{\,\small =\,}-cos\theta \hspace{20pt}\left\{\small\textsf{加法定理による導出。}\right\} \\[5pt] cos(\pi-\theta){\,\small =\,}{\class{Underline-L}{cos\pi cos\theta{\,\small +\,}sin{\pi} sin\theta{\,\small =\,}cos{\small\displaystyle\frac{-1}{1}}cos\theta{\,\small +\,}sin{\small\displaystyle\frac{0}{1}}sin\theta}}{\,\small =\,}-cos\theta \hspace{20pt}\left\{\small\textsf{加法定理による導出。}\right\} \\[5pt] sin(\pi+\theta){\,\small =\,}{\class{Underline-L}{sin\pi cos\theta{\,\small +\,}cos\pi sin\theta{\,\small =\,}sin{\small\displaystyle\frac{0}{1}}cos\theta{\,\small +\,}cos{\small\displaystyle\frac{-1}{1}}sin\theta}}{\,\small =\,}-sin\theta \hspace{20pt}\left\{\small\textsf{加法定理による導出。}\right\} \\[5pt] sin(\pi-\theta){\,\small =\,}{\class{Underline-L}{sin\pi cos\theta{\,\small -\,}cos\pi sin\theta{\,\small =\,}sin{\small\displaystyle\frac{0}{1}}cos\theta{\,\small -\,}cos{\small\displaystyle\frac{-1}{1}}sin\theta}}{\,\small =\,}\hspace{20pt}sin\theta \hspace{20pt}\left\{\small\textsf{加法定理による導出。}\right\} \\[5pt] tan(\pi+\theta){\,\small =\,}{\class{Underline-L}{{\small\displaystyle\frac{sin(\pi+\theta)}{cos(\pi+\theta)}}{\,\small =\,}{\small\displaystyle\frac{-sin\theta}{-cos\theta}}}}{\,\small =\,}\hspace{20pt}tan\theta\hspace{20pt}\left\{\small\textsf{三角関数の相互関係式と上記の還元公式より導出。}\right\} \\[5pt] tan(\pi-\theta){\,\small =\,}{\class{Underline-L}{{\small\displaystyle\frac{sin(\pi-\theta)}{cos(\pi-\theta)}}{\,\small =\,}{\small\displaystyle\frac{sin\theta}{-cos\theta}}}}{\,\small =\,}-tan\theta\hspace{20pt}\left\{\small\textsf{三角関数の相互関係式と上記の還元公式より導出。}\right\} \end{array}\right.\)
