正弦定理 とは、三角形の内角の正弦 \(sin\) からその対辺の長さを求める定理である。
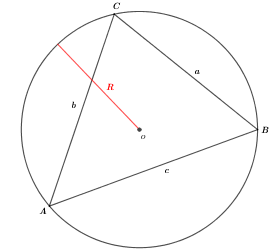
上図1より、\(\left\{\begin{array}{l} \textsf{直角三角形の高さの値は$sin\,\theta$ である。$~~\color{yellow}cf\,\to$ $\small\color{gray}{\textsf{雛形数学 > 三角関数 > }}$ $\href{https://showanojoe.com/template-math/trigonometric-function/cosine-trigonometric-ratio/}{\small\textsf{余弦($cos\,\theta$),$\,$正弦($sin\,\theta$),$\,$正接($tan\,\theta$)}}$ } \\[15pt] b\times\,sinA(\displaystyle\frac{b}{1}\times\,\frac{b\,sinA}{sinA})=a\times\,sinB(\frac{a}{1}\times\,\frac{a\,sinA}{sinA})\;\textsf{すなわち、$ b\,sinA=a\,sinB \;$を式変形すると$\;\frac{a}{sinA}=\frac{b}{sinB}\;$となる。} \\[15pt] \displaystyle\frac{b}{sinB}=\frac{c}{sinC,}\hspace{10pt} \frac{c}{sinC}=\frac{a}{sinA}\;\textsf{も同様である。} \\[15pt] \displaystyle\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}\textsf{が導かれる。}\end{array}\right.\)
正弦定理の公式\(~\tiny\displaystyle{\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=}\,2R\)
図1と図1からのブロック を踏まえて、図2からのブロックで 正弦定理の公式 を証明しよう。
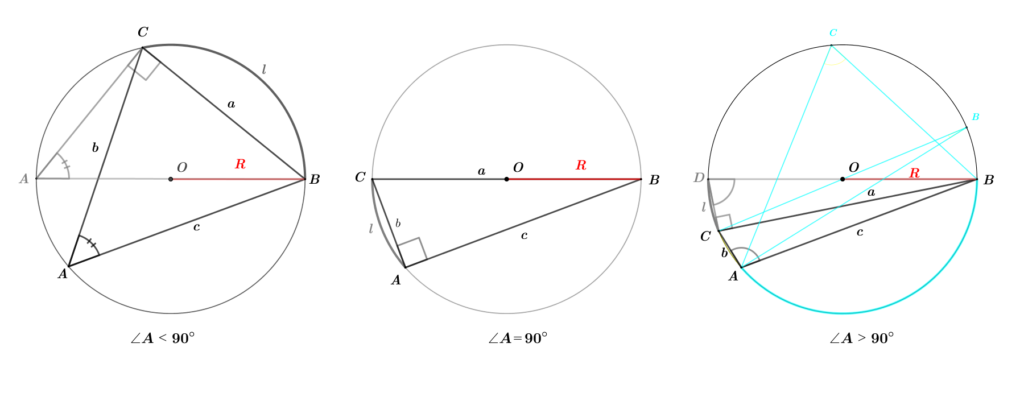
図2から\(\left\{\begin{array}{l}\textsf{$\angle{A}$ が鋭角($\small\angle{A}\,<\,90^\circ$) の証明}\left\{\begin{array}{l}\textsf{円弧 $\color{darkgray}l$ を基底とした円周角 $\angle{A}$ と $\angle{\color{darkgray}A}$ は等しい。} \\ \hookrightarrow ~~~\color{yellow}cf\,\to \small\color{lightgray}{\textsf{雛形数学 > 補足資料 > 円周角・中心角と円に内接する四角形 > }}\href{https://showanojoe.com/template-math/supplementary-material/1-1/#1}{\small\textsf{円周角・中心角}} \\[5pt] \textsf{$\triangle{{\color{darkgray}A}BC}$ において、$sin{\color{darkgray}A}=\small\displaystyle\frac{a}{2\color{red}R}~( \color{red}R $ は 外接円 の半径。)} \\[5pt] \textsf{上の式を変形すると $\small\displaystyle\frac{a}{ sin\color{darkgray}A }=2 \color{red}R $ となる。$\angle{B},\;\angle{C}$ も同様である。} \\[5pt] \textsf{よって、 $~\small\displaystyle{\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=}\,2R$ となる。} \end{array}\right. \\[10pt] \textsf{$\angle{A}$ が直角($\small\angle{A}\,=\,90^\circ$) の証明}\left\{\begin{array}{l} \textsf{$\angle{A}$ が鋭角($\small\angle{A}\,<\,90^\circ$) の証明より、} \\[5pt] \angle{A}=90^\circ\,\to\,sin90^\circ=1 \\ \hookrightarrow~~~\color{yellow}cf\,\to\small\color{lightgray}{\textsf{雛形数学 > 三角関数 > }} \href{https://showanojoe.com/template-math/trigonometric-function/cosine-trigonometric-ratio/}{\small\textsf{余弦($cos\,\theta$),$\,$正弦($sin\,\theta$),$\,$正接($tan\,\theta$)}} \\[5pt] \small\displaystyle\frac{a}{1}=2 {\color{red}R}\,\to\, \small\displaystyle\frac{a}{sinA}= 2\color{red}R \\[5pt] \angle{B},\;\angle{C} \textsf{については $\angle{A}$ が鋭角($\small\angle{A}\,<\,90^\circ$) の円周角を用いた証明に倣う。} \\[5pt] \textsf{よって $~\small{\displaystyle{\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}}}=\,2R$ 。 } \end{array}\right. \\[10pt] \textsf{$\angle{A}$ が鈍角($\small\angle{A}\,>\,90^\circ$) の証明}\left\{\begin{array}{l}\textsf{$\triangle{ABC}$ において、四角形 $AB{\color{darkgray}D}C$ を応用する。} \\[5pt] \textsf{円に内接する四角形の向かい合う角の和は $180^\circ$ なので、$\angle{a}+\angle{\color{darkgray}D}=180^\circ$} \\ \hookrightarrow~~~\color{yellow}cf\,\to \small\color{lightgray}{\textsf{雛形数学 > 補足資料 > 円周角・中心角と円に内接する四角形 > }}\href{https://showanojoe.com/template-math/supplementary-material/1-1/#2}{\small\textsf{円に内接する四角形}} \\[5pt] \textsf{式変形した $\angle{\color{darkgray}D}=180^\circ -\angle{A}$ の $sin(180^\circ -A)$ は $sinA$ になる。} \\ \hookrightarrow~~~\color{yellow}cf\,\to \small\color{lightgray}{\textsf{雛形数学 > 三角関数 > 三角比から三角関数へ > }\href{https://showanojoe.com/template-math/trigonometric-function/from-trigonometric-ratio-to-trigonometric_function/1-1/#2}{\small\textsf{$\measuredangle{\alpha}$ の平面座標}}} \\[5pt] sin{\color{gray}D}=sin(180^\circ -A)=\boldsymbol{sinA=\small\displaystyle\frac{a}{2\color{red}R}}\textsf{ の太字の数式を式変形して、}~\small\displaystyle\frac{a}{sinA}=2\color{red}R \\[5pt] \textsf{$\angle{B},~\angle{C}$ については、上述の $\angle{A}$ が鋭角($\small\angle{A}\,<\,90^\circ$) の証明 を参照。} \\[5pt] \textsf{よって $~\small{\displaystyle{\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}}}{\small\,=\,}\,2{\color{red}R}$ 。 } \end{array}\right. \end{array}\right.\)
