三平方の定理 とは、直角三角形 の\(2\)辺の長さから他の\(1\)辺の長さを特定する定理である。

三平方の定理の定義式\(\hspace{10pt}\sqrt{c^{\scriptsize 2}}{\scriptsize\,=\,}\sqrt{a^{\scriptsize 2}{\scriptsize\,+\,}b^{\scriptsize 2}}\)
\(\left\{\begin{array}{l}\textsf{上図$1$の直角三角形は、底辺を $a$、高さを $b$、斜辺は $c$ とする。} \\ \textsf{底辺を $x$ とおくと、$\sqrt{c^{\scriptsize 2}}{\scriptsize\,=\,}\sqrt{x^{\scriptsize 2}{\scriptsize\,+\,}b^{\scriptsize 2}}\hspace{10pt}\Rightarrow\hspace{10pt}\sqrt{c^{\scriptsize 2}}{\scriptsize\,=\,}\sqrt{x^{\scriptsize 2}}{\scriptsize\,+\,}\sqrt{b^{\scriptsize 2}}\hspace{10pt}\hspace{10pt}\Rightarrow\hspace{10pt}\sqrt{x^{\scriptsize 2}}{\scriptsize\,=\,}\sqrt{c^{\scriptsize 2}{\scriptsize\,-\,}b^{\scriptsize 2}}$} \\ \textsf{高さを $x$ とおくと、$\sqrt{c^{\scriptsize 2}}{\scriptsize\,=\,}\sqrt{a^{\scriptsize 2}{\scriptsize\,+\,}x^{\scriptsize 2}}\hspace{10pt}\Rightarrow\hspace{10pt}\sqrt{c^{\scriptsize 2}}{\scriptsize\,=\,}\sqrt{a^{\scriptsize 2}}{\scriptsize\,+\,}\sqrt{x^{\scriptsize 2}}\hspace{10pt}\hspace{10pt}\Rightarrow\hspace{10pt}\sqrt{x^{\scriptsize 2}}{\scriptsize\,=\,}\sqrt{c^{\scriptsize 2}{\scriptsize\,-\,}a^{\scriptsize 2}}$}\end{array}\right.\)
三平方の定理の証明
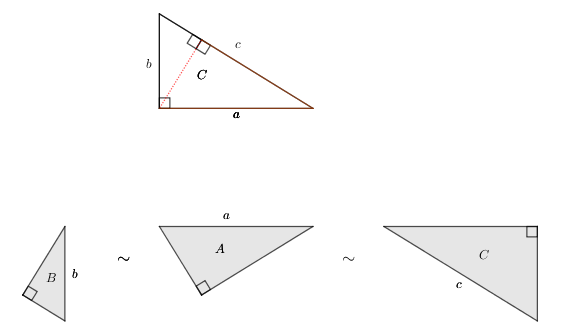
\(\left\{\begin{array}{l}\textsf{直角三角形 $C$ の直角から対辺の斜辺に垂直な線分を引き、直角三角形$B,A$ を導出する。} \\[10pt] \textsf{$C$ はもとより、$B$ の斜辺が $C$ の高さ、$A$ の斜辺が $C$ の底辺となる$3$つの直角三角形は互いに 相似(同形) である。} \\ \hspace{250pt}\left\{\small\textsf{$\sim$ は互いに相似を意味する記号。}\right\} \\[10pt] \textsf{相似の対応する辺の長さの比を 相似比 という。ここでは直角三角形$B,A,C$の斜辺の相似比 $b:a:c$ 。} \\[10pt] \textsf{三角形を $m$倍 に拡大すると、底辺、高さ、斜辺共に $m$倍になり、面積は $m^{\scriptsize{\class{Boldfont}{2}}}$倍 になる。 } \\ \hspace{100pt}\left\{\begin{array}{l}\small\textsf{底辺、高さ共に$1$の直角二等辺三角形を$m$倍した面積比を例にとると理解しやすい。} \\ \small\textsf{ちなみに、三角形の面積の公式は 底辺$\times$高さ$\div 2$。}\end{array}\!\!\!\right\} \\[10pt] \textsf{底辺の相対比が $b:a:c$ の$3$つの直角三角形$B,A,C$の面積$S{\scriptsize b},S{\scriptsize a},S{\scriptsize c}$は $S{\scriptsize b}:S{\scriptsize a}:S{\scriptsize c}{\scriptsize\,=\,}b^{\scriptsize{\class{Boldfont}{2}}}:a^{\scriptsize{\class{Boldfont}{2}}}:c^{\scriptsize{\class{Boldfont}{2}}}$ の比となる。} \\[10pt] \textsf{直角三角形$B,A$は$C$から派生したものなので、$S{\scriptsize b}{\scriptsize\,+\,}S{\scriptsize a}{\scriptsize\,=\,}S{\scriptsize c}\hspace{5pt}$すなわち$\hspace{5pt}b^{\scriptsize{\class{Boldfont}{2}}}{\scriptsize\,+\,}a^{\scriptsize{\class{Boldfont}{2}}}{\scriptsize\,=\,}c^{\scriptsize{\class{Boldfont}{2}}}\hspace{10pt}\Rightarrow\hspace{10pt}\sqrt{c^{\scriptsize 2}}{\scriptsize\,=\,}\sqrt{a^{\scriptsize 2}{\scriptsize\,+\,}b^{\scriptsize 2}}\hspace{5pt}$ が成り立つ。 }\end{array}\right.\)
